线性回归模型，含线性回归的定义、推导过程、python代码实现以及结果展示。非常详细的线性回归模型解释

一：线性回归简介

        依据自变量的数量分为一元线性回归和多元线性回归。

                       

                       

                其中：   

                   ：是因变量（要预测的变量）

                 ：是自变量，它表示的是不同维度的变量值。（用来预测因变量的变量）

                 ：是截距

                ：是不同维度自变量的系数（斜率）

                 ：是误差项，表示模型无法解释的部分

二：一元线性回归模型

        1、推导过程

        已知一组数据和,由回归的定义可知，目的是要找到一个回归方程：，使得计算得到的尽可能接近真实数据。

        一元方程组：，其中Y,X是向量 

                         

则令,      

变形后的公式为：    注意此时的X是n*2维向量，A是2*1维向量。

定义残差e：

             , 是n*1维向量。只有当的值最小时，回归方程求的Y与真实值之间的误差最小。求最小。

残差平方和：定义为残差的L2范数的平方。该方法也成为最小二乘法。

 

展开可以得到：

 

由于得到的是1*1的向量，所以

                                

则可得到：

要求一个A，使得残差平方和最小，由极值点求法知道，当时，RSS(A)取得最小值。

                              

对    求导要用到：                                                 

对求导数要用到该公式：  

当时，可得，该方程也被称作正规方程

        如果可逆，则最优解：

        如果不可逆，说明方程组中存在两个以上的方程成线性关系（成比例）。这时候我们应该用其他方式求线性回归的解。在此先不做讨论。

2、代码展示

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 生成随机数据.相同的种子生成的数据是一样的。
np.random.seed(0)
#rand(100,1)生成形状为100*1的大小在[0，1）之间的数据.100行1列。
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

# 向 X 添加偏置项。np.c_[]:对两个矩阵按列合并。
# np.ones(100,1)：也是100行1列全为1的矩阵。
#合并后就是100*2的矩阵。由于1的列矩阵是在前面，所以求解出来第一个参数是B，第二个才是A
X_b = np.c_[np.ones((100, 1)), X]  # 在 X 矩阵中添加一列1
# 使用 NumPy 。先求x转置*x的逆，再乘x的转置，再乘y，即最优解A。
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
# 输出拟合的参数
print("拟合的参数：", theta_best)

# 进行预测。两个点：一个0点，一个2.
X_new = np.array([[0], [2]])
X_new_b = np.c_[np.ones((2, 1)), X_new]  # 在 X_new 矩阵中添加一列1
y_predict = X_new_b.dot(theta_best)
print("预测值：", y_predict)

# # 绘制数据和拟合直线
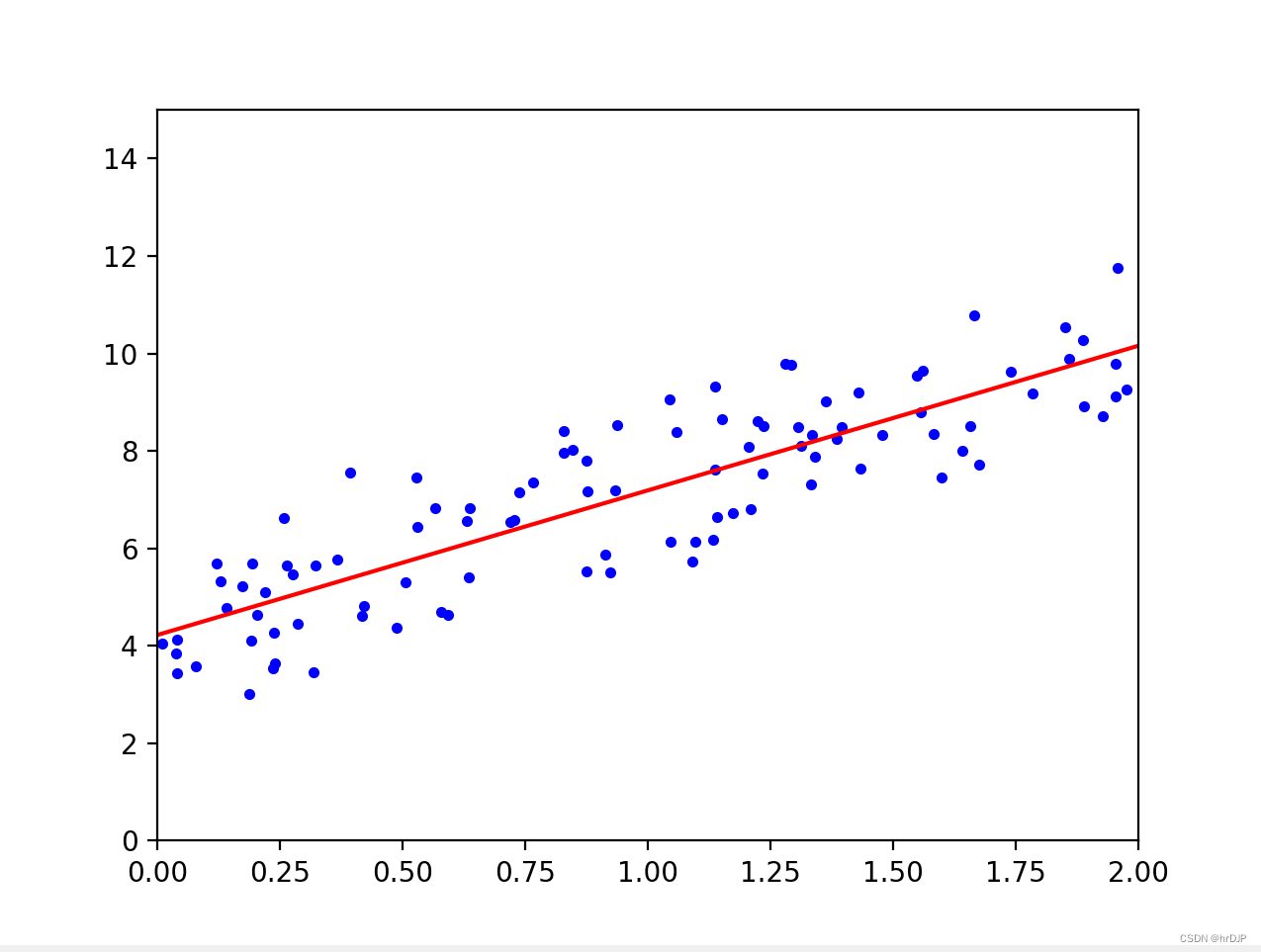
plt.plot(X, y, "b.")
plt.plot(X_new, y_predict, "r-")
plt.axis([0, 2, 0, 15])
plt.show()

三：多元回归模型

        1、推导过程

        多元方程： ，其中Y,X,B是向量         

                     

  

则令 

    变形后的公式为：    注意此时的X是n*p维向量，A是p*1维向量。后面的推导与一元的函数一样。有线性代数基础应该很容易看懂。下面代码展示的是使用 scikit-learn库中的线性回归模型进行回归预测。模型库封装更加完善，推荐使用库中的方法，特别是当不可逆时，库中有解决方案。sklearn.linear_model.LinearRegression()

2、代码展示

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

# 生成随机数据.相同的种子生成的数据是一样的。
np.random.seed(0)
#rand(100,1)生成形状为100*1的大小在[0，1）之间的数据.100行1列。
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

# 使用 scikit-learn 进行线性回归
lin_reg = LinearRegression()
lin_reg.fit(X, y)

# 输出拟合的参数
print("截距：", lin_reg.intercept_)
print("斜率：", lin_reg.coef_)

# 进行预测。两个点：一个0点，一个2.
X_new = np.array([[0], [2]])
X_new_b = np.c_[np.ones((2, 1)), X_new]  # 在 X_new 矩阵中添加一列1
print("预测值：", lin_reg.predict(X_new))

# 绘制数据和拟合直线
plt.plot(X, y, "b.")
plt.plot(X_new, lin_reg.predict(X_new), "r-")
plt.axis([0, 2, 0, 15])
plt.show()

四：结果展示