时间序列分析1：python里用AR自回归模型分析预测时间序列

Autoregression / AR，就是用前期数据来预测后期数据的回归模型，所以叫做自回归模型。
它的逻辑简单，但对时间序列问题能够做出相当准确的预测。<原文链接这里>

1）自回归函数

$$y{\hat{}}_t=b_0+b_1{y}_{t-1}+...+b_n{y}_{t-n},其中n<t$$
只有在数据平稳/弱平稳的基础上，才能进行实现序列分析

正式的说，如果一个时间序列$x_t$ 的一阶矩和二阶矩（即均值和方差）具有时间不变性，则称它为弱平稳的。弱平稳性是很重要的，因为它为预测提供了基础框架。
——《金融数据分析导论：基于R语言》2.1 平稳性

2）上例子

1. 首先取数&画图

import pandas as pd
import matplotlib.pyplot as plt

df = pd.read_csv('https://raw.githubusercontent.com/jbrownlee/Datasets/master/daily-min-temperatures.csv',
				 index_col=0, parse_dates=True)
print(df.head())
df.plot()
plt.show()

# 结果如下
            Temp
Date            
1981-01-01  20.7
1981-01-02  17.9
1981-01-03  18.8
1981-01-04  14.6
1981-01-05  15.8

从上图可知温度序列是弱平稳的（weakly stationary）；但是肉眼看不精确是不是平稳的，此时ADF Test/ Augmented Dickey-Fuller Test就排上用场了，其原假设H0：存在单位根/UNIT ROOT（即数据不平稳）

from statsmodels.tsa.stattools import adfuller
a = df.Temp
print(adfuller(a,    # 下述参数均为默认值
				maxlag=None, 
				regression='c', 
				autolag='AIC',   # 自动在[0, 1,...,maxlag]中间选择最优lag数的方法；
				store=False, 
				regresults=False)
				)

# 结果如下
(-4.444804924611687,   #  AIC标准下得到的统计值，用于和下边 1%，5%，和10%临界值比较。但更方便的是直接用下边的p值
 0.00024708263003611164,   #  AIC标准下的p值，即原假设成立的概率
 20,     # usedlag: AIC标准下adfuller用的lags
 3629,   # nobs: 本次检测用到的【观测值】个数;
{'1%': -3.4321532327220154,   # 1%标准下的临界值
'5%': -2.862336767636517, 
'10%': -2.56719413172842}, 
16642.822304301197) # icbest: The maximized information criterion if autolag is not None.

由p值可以看出，原假设成立的概率极低，我们应该拒绝原假设。即数据平稳。

adfuller函数官方文档备注：
Augmented Dickey-Fuller的原假设是存在单位根，备择假设是不存在单位根。如果p-value大于临界值，那么我们就不能拒绝有一个单位根存在。

p-value是通过MacKinnon 1994年的回归曲面近似得到的，但使用的是更新的2010年表。

2. 快速查看数据是否适合AR模型

from pandas.plotting import lag_plot
lag_plot(df)   # 默认lag=1
plt.show()
# 结果如图所示：

如上图所示，$y_{t+1}$和$y_t$明显相关。当然我们能通过计算，得到相关系数是0.77和显著性水平0。

from scipy.stats import pearsonr

a = df.Temp
b = df.Temp.shift(1)

print(pearsonr(a[1:], b[1:]))

# 结果如下
(0.7748702165384458, 0.0)

3. 上边是很好的检测方法。但是如果我们想同时查看$Y_t$和$Y_{t-1}$,…,$Y_{t-n}$的相关性，重复n次就太繁琐了。

下面介绍一个一次性画出n多Lag的自回归系数方法：statsmodels.graphics.tsaplots.plot_acf()

from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
fig, axes = plt.subplots(2,1)

fig, axes = plt.subplots(2, 1)
plot_acf(df['Temp'], ax=axes[0])
plot_pacf(df['Temp'], ax=axes[1])

plt.tight_layout()
plt.show()

4. 最后，到此为止我们就知道如何查看时间序列数据的自相关性了。接下来看如何用对它建立模型。

import pandas as pd
import numpy as np
from statsmodels.tsa.ar_model import AutoReg
import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error as MSE

df = pd.read_csv('e:/daily-min-temperatures.csv',
                 index_col=0, parse_dates=True)
"""把模型数据分为train和test，分别用来训练模型和对比模型预测结果"""
x = df.Temp.values
train, test = x[:-20], x[-20:]  # test的个数设定为7

"""训练模型得到所需参数：AR的滞后项个数p，和自回归函数的各个系数"""
p = 29  # 调参可以参看下文的链接
# 即时间序列模型中常见的p，即AR(p), ARMA(p,q), ARIMA(p,d,q)中的p。
# p的实际含义，此处得到p=29，意味着当天的温度由最近29天的温度来预测。
model_fit = AutoReg(train, lags=p).fit()
params = model_fit.params

history = train[-p:]   
history = np.hstack(history).tolist()  # 唯一的目的就是接下来通过append(test[i])实时更新history
# 也可以用history = [history[i] for i in range(len(history))] ，
# （append函数不适用于np.narray类型的history）

predictions = []
for t in range(len(test)):
	yhat = params[0]
	for i in range(p):
		yhat += params[i+1] * history[-1-i]  # history滚动提供lags
	predictions.append(yhat)
	history.append(test[t])
print(np.mean((np.array(test) - np.array(predictions))**2))  # 得到mean_squared_error, MSE
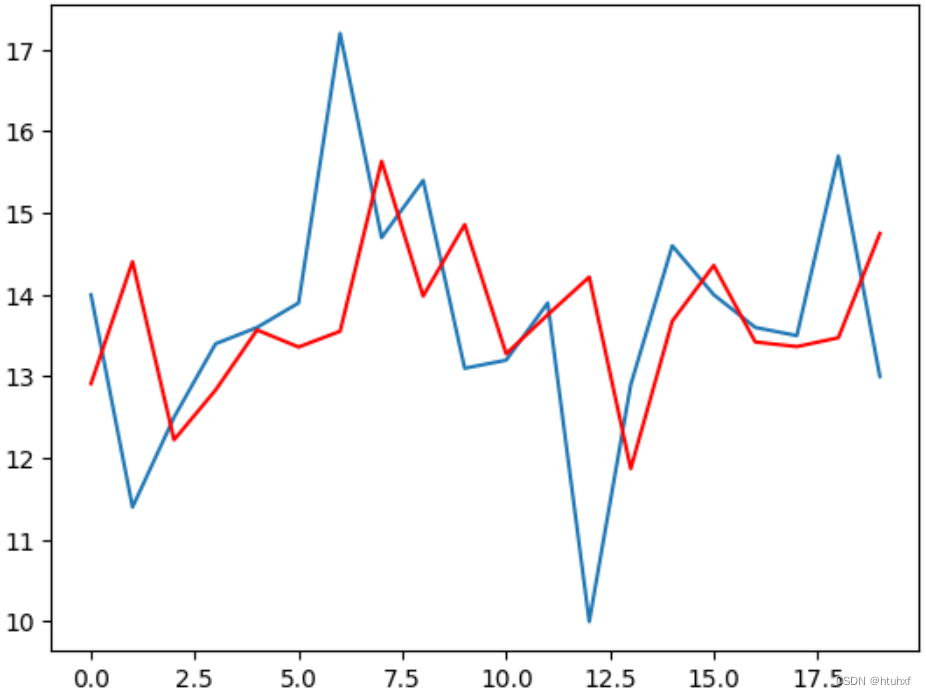
plt.plot(test)
plt.plot(predictions, color='r')
plt.show()

附注：

- 2个随机变量X和Y的pearson线性相关系数定义为：

$${\rho }_{x,y}=\frac{Cov(X,Y)}{\sqrt{Var(X)Var(Y)}}=\frac{E[(X-{\mu }_x)(Y-{\mu }_y)]}{\sqrt{E(X-{\mu }_x{)}^{2}E(Y-{\mu }_y{)}^2}}$$
– 具体到样本：
$${\hat{\rho }}_{x,y}=\frac{{\sum }_{t=1}^T[(x_t-\bar{x})(y_t-\bar{y})]}{\sqrt{{\sum }_{t=1}^T(x_t-\bar{x}{)}^2{\sum }_{t=1}^T(y_t-\bar{y}{)}^2}}$$

- 调参：可看下ARIMA为例的链接；