傅里叶变换及其实现（MATLAB）

傅立叶变换

傅立叶变换是一种常见的分析方法，傅立叶变换将满足一定条件的函数表示为一些函数的加权和（或者积分）。可以分为四个类别：
1. 非周期连续性信号
对应于傅里叶变换，频域连续非周期
2. 周期性连续性信号
对应于傅立叶级数，频域离散非周期
3. 非周期离散信号
对应于DTFT（离散时间傅立叶变换），频域连续周期
4. 周期性离散信号
对应于DFT（离散时间傅立叶变换），频域离散周期

傅立叶级数

首先从傅立叶级数开始分析，傅立叶级数是将一个信号在一组正交基上进行分解的体现。

$$x(t) = \sum_{k=-\infty}^{+\infty}a_{k}e^{jk\omega_{0}t}$$
$$a_{k} = \frac{1}{T} \int_{-T/2}^{T/2}x(t)e^{-jk\omega_{0}t}dt$$

连续时间傅立叶变换

$\omega_{0} = \frac{2\pi}{T}$，当$T\to\infty$时，$\omega_{0}\to 0$；
令$X(j\omega)$是$Ta_{k}$的包络，用$k\omega_{0}\to\omega$，推出：
正变换：

$$X(j\omega) = \int_{-\infty}^{+\infty}x(t)e^{-jk\omega_{0}t}dt$$
其中 $a_{k}$是 $X(j\omega)$的等距离采样， $a_{k} = \frac{1}{T}X(jk\omega_{0})$
所以当 $T\to\infty$时， $\omega_{0}\to 0$，可以推出：
$x(t) = \sum a_{k}e^{jk\omega_{0}t} = \sum \frac{1}{T}X(jk\omega_{0})e^{jk\omega_{0}t} = \sum \frac{1}{2\pi}X(jk\omega_{0})e^{jk\omega_{0}t}\omega_{0}$
极限时转变为积分：
逆变换：
$$x(t) = \frac{1}{2\pi}\int_{-\infty}^{+\infty} X(j\omega)e^{j\omega t}d\omega$$

离散时间傅立叶变换

离散时间傅立叶变换在频域上是连续的，但由于计算机无法表示无限长的时间片段，已经无法表示全部频率，一般取一定频域的分量。
正变换：

$$X(e^{j\omega}) = \sum_{n=-\infty}^{+\infty}x[n]e^{-j\omega n}$$
逆变换：
$$x[n] = \frac{1}{2\pi} \int_{2\pi}^{}X(e^{j\omega})e^{j\omega n}d\omega$$

离散傅立叶变换

只有离散傅立叶变换在频域和时域都是离散的，即计算机可以处理的，因此DFT是可以实际进行编程并实用的。DFT的信号首先要进行截断，因为能处理的信号必须是有限的；然后对信号进行采样，对频谱进行离散化。
正变换：

$$X(k) = \sum_{n=0}^{N-1}x(n)e^{-j\frac{2\pi}{N}nk}$$
逆变换：
$$x(n) = \frac{1}{N}\sum_{k=0}^{N-1}X(k)e^{j\frac{2\pi}{N}nk}$$

二维傅立叶变换

$$F(u,v) = \sum_{x=0}^{M-1} \sum_{y=0}^{N-1}f(x,y)e^{-j2\pi(ux/M+vy/N)}$$
$$f(x,y) = \frac{1}{MN}\sum_{x=0}^{M-1} \sum_{y=0}^{N-1}F(u,v)e^{j2\pi(ux/M+vy/N)}$$

傅立叶变换实现

只有离散傅里叶变换才可以实现，在MATLAB中实现有fft，fft2进行傅里叶变换，同样可以手动进行变换。

一维傅立叶变换

基于FFT

%  xn是信号，n是坐标，N是点数
%  N =8;
%  n = [0:1:N-1];
%  xn = 0.5.^n;        % 指数信号
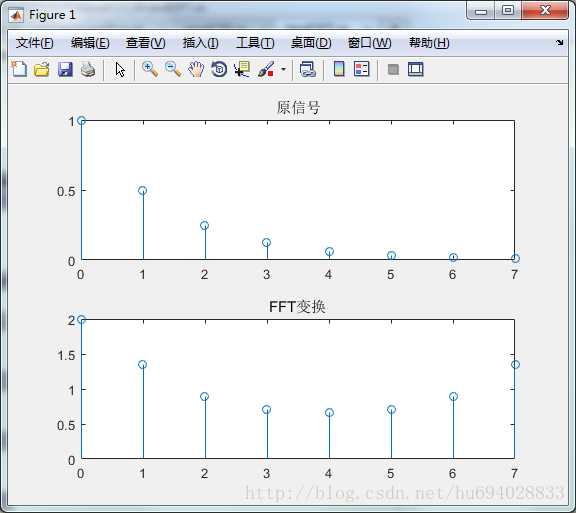
function [] = DFTusefft(xn,n,N)
    figure(1);
    Xk=fft(xn,N);      % 傅立叶变换
    subplot(211);
    stem(n,xn);
    title('原信号');

    subplot(212);
    stem(n,abs(Xk));
    title('FFT变换')
end

DFT公式

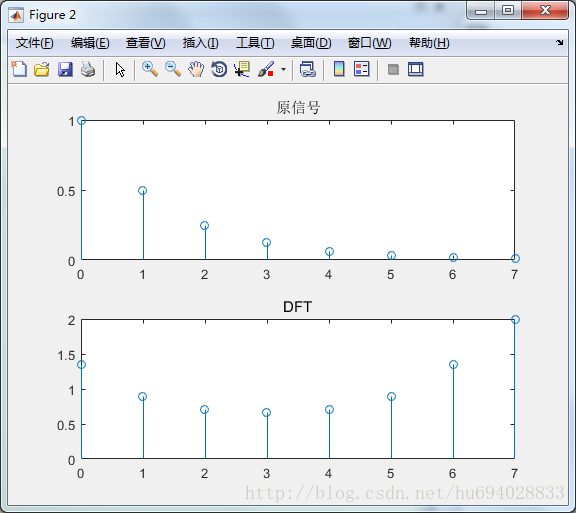
function [] = DFT(xn,n,N)
    Xk = zeros(1,N);    
    for k=1:N
        sn =0.0;
        for i=1:N
            sn = sn+xn(i)*exp(-j*2*pi*i*k/N);
        end
        Xk(k) = sn;
    end
    figure(2);
    subplot(211);
    stem(n,xn);
    title('原信号');

    subplot(212);
    stem(n,abs(Xk));
    title('DFT')
end

DTFT
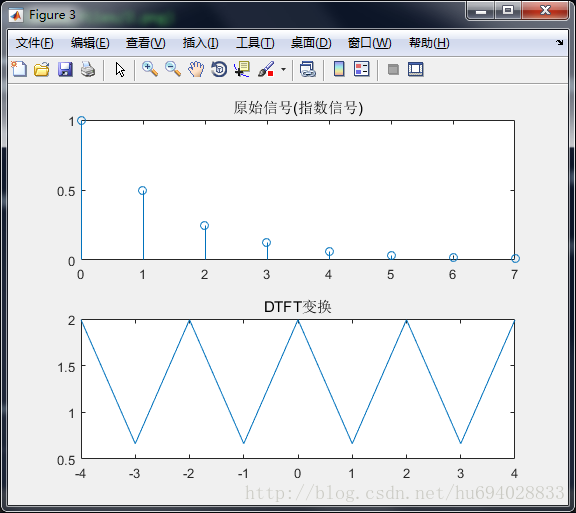
由于DTFT的频域是连续的而且是无穷的，当我们选择的最高频域足够高时，可以基本代表信号特征，可以进行编程。

function [] = testDTFT(xn,n,N)
    figure(3);
    w=[-800:1:800]*4*pi/800;     %频域共-800----+800 的长度（本应是无穷，高频分量很少，故省去）    
    w = [-N/2:1:N/2]*4*pi*2/N;
    X=xn*exp(-j*(n'*w));         %求dtft变换，采用原始定义的方法，对复指数分量求和而得
    subplot(211)
    stem(n,xn);
    title('原始信号(指数信号)');
    subplot(212);
    plot(w/pi,abs(X));
    title('DTFT变换')
end

二维傅立叶变换

原始图像

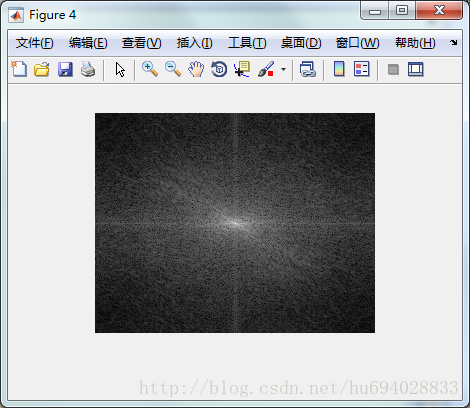
使用fft2

function [] = imagefft()
    I=imread('lenna.jpg');
    I=rgb2gray(I);
    I=im2double(I);
    F=fft2(I);
    F=fftshift(F);
    F=abs(F);
    T=log(F+1);
    figure(4);
    imshow(T,[]);
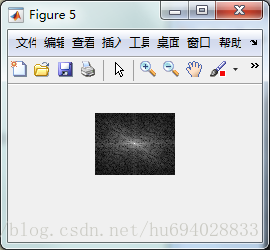
end

使用二维傅立叶变换公式
速度很慢

function [] = imageDFT()
    I=imread('lenna_s.jpg');
    I=rgb2gray(I);
    I=im2double(I);
    [x,y] = size(I);
    ans = ones(x,y);
    com = 0+1i;
    for u =1:x
        for v= 1:y
            sn =0;
            for i=1:x                
                for j=1:y
                    sn = sn+I(i,j)*exp(-com*2*pi*(u*i/x+v*j/y));
                end
            end
            ans(u,v) = sn;
        end
    end
    F=fftshift(ans);
    F= abs(F);
    F=log(F+1);
    figure(5);
    imshow(F,[]);
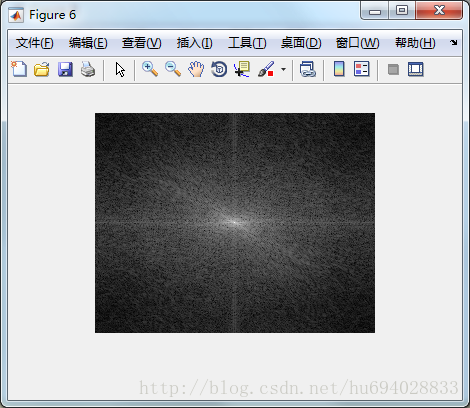
end

优化二维傅立叶变换
先按列进行傅里叶变换，再对行进行傅立叶变换，简化计算。

function [] = imageDFT2()
    I=imread('lenna.jpg');
    I=rgb2gray(I);
    I=im2double(I);
    [x,y] = size(I);
    Ax = ones(x,y);
    ans = ones(x,y);
    com = 0+1i;
    % 对每一列进行DFT
    for k =1:x        
        for m=1:y
            sn =0;
            for n =1:x
                sn =sn + I(n,m)*exp(-com*2*pi*k*n/x);
            end
            Ax(k,m) = sn;
        end
    end
    % 对每一行进行DFT
    for l =1:y
        for k =1:x
            sn =0;
            for m=1:y
                sn = sn+Ax(k,m)*exp(-com*2*pi*l*m/y);
            end
            ans(k,l) = sn;
        end
    end    
    F=fftshift(ans);
    F= abs(F);
    F=log(F+1);
    figure(6);
    imshow(F,[]);
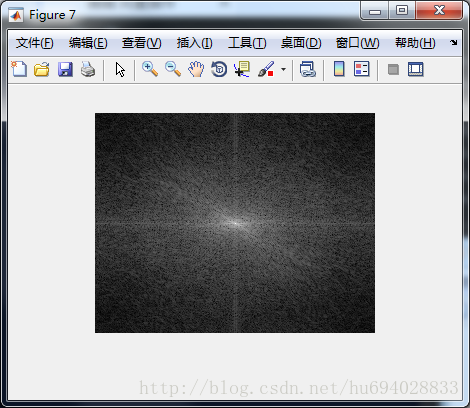
end

优化二维傅立叶变换
将按列进行傅里叶变换中使用DFT改为使用fft，速度提升很快。

function [] = imageDFT2fft()
    I=imread('lenna.jpg');
    I=rgb2gray(I);
    I=im2double(I);
    [x,y] = size(I);
    Ax = ones(x,y);
    ans = ones(x,y);
    com = 0+1i;
    % 对每一列进行DFT  
    for m=1:y
        Ax(:,m) = fft(I(:,m));
    end
    % 对每一行进行DFT    
    for k=1:x
        ans(k,:) = fft(Ax(k,:));
    end
    F=fftshift(ans);
    F= abs(F);
    F=log(F+1);
    figure(7);
    imshow(F,[]);
end

github地址

如有错误，欢迎指出~