数二真题强化

s# 初等数学

平方根

√￣是算数平方根，一定>=0

三角函数

cotx=$\frac{1}{tanx}$
(arcsinx)'=$\frac{1}{\sqrt{1-x^2}}$
在(0,$\frac{\pi }{2}$)，tanx>x>sinx
x=$\sqrt{2}$sint =>t=arcsin$\frac{x}{\sqrt{2}}$

反三角函数

用换元时，尽量用x=sint，t=arcsinx

复合函数

f(u)的表达式中应含有u，例如f(x²)的表达式应含有x²，将x²看为u

一元二次方程

顶点坐标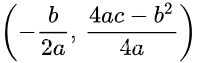

高等数学

极限

震荡无穷大不是无穷大，即无界不一定是无穷大

数列

数列收敛，不一定单调，可能在收敛值震荡，如n->$\infty$，(-1)ⁿ/n收敛于0，但在0左右震荡
单调有界必收敛，前提是f(x)的x单调

x->0的等价无穷小：
arcsinx~x
x-sinx~$\frac{1}{6}$x³
tanx-x~$\frac{1}{3}$x³
x-arctanx~$\frac{1}{3}$x³
(1+x)^a-1~ax

极限计算

1、极限非零因子先求出来，可用于平方差公式a²-b²，让有平方的分子有理化，让分母直接代入求出。如分子有1-$\sqrt{cosx}$
2、有理加减可以先用后验，各部分极限都存在即可
3、洛必达和等价无穷小代换不能同一步进行

连续与间断点

找间断点：1、所在分母，为0的点；2、所在分子，使函数趋于无穷的点
在x₀间断，则在x₀去心邻域有定义，但在x₀定义可有可无，但在x₀处函数一定是断了

可去间断点

可去间断点需满足f(x)在x₀处无定义，或在x₀处有定义但不等于函数f(x)在x₀的左右极限。

导数与微分

常用导数

导数

(ln|x|)'=$\frac{1}{x}$

不可跨：用导数定义求导时，严格是-f(x₀)，而不是任何其他的诸如-f(-x₀)、-f(x₀-a)
不可跨越x₀

导数定义limf(x)-f(0)的x可以是其他形式，如x³、e^x

微分

方程求微分dy
解：隐函数方程两边求导得y’，dy=y’dx

微分中值定理及导数应用

泰勒

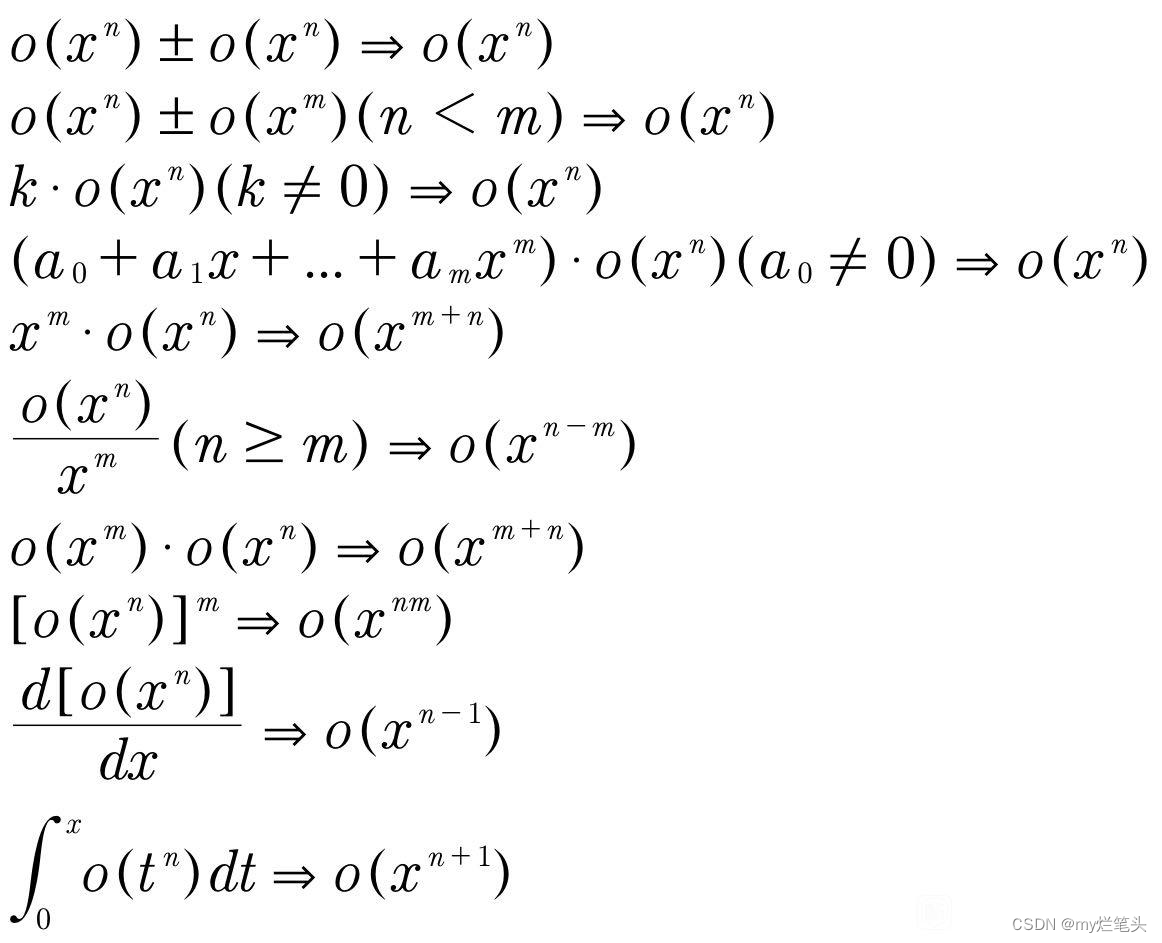
单调性

1、用f’(x)>0判断单调性是在区间上，某点f’(x₀)>0无法得出x₀邻域单调性
2、单调区间可以间断，且是第一类间断点
3、在区间上，或x₀邻域，f’(x) $\ge$ 0，（=0是有限点），单调增加

极值

极值点可能是驻点也可能是连续但不可导点
1、极值第一充分条件可用于连续不可导点的极值判断
2、极值第二充分条件f’'(x₀)只能在x₀二阶可导前提下判断

凹凸性

f’‘(x)>0凹可能递增也可能递减；f’'(x)<0凸可能递增也可能递减

拐点

第二充分条件：若y’‘(x₀)=0，且y’‘’(x₀) $\ne$ 0 则x₀为拐点

渐近线

函数在一侧水平渐近线与斜渐近线存在性互斥，但一侧没有还要考虑另一侧
如x→+$\infty$有水平无斜，但x→-$\infty$有斜无水平

铅直

铅直找无定义点，分母为0点

不定积分

∫$\frac{1}{x^2-6x+13}$dx~$\frac{1}{a}$arctan$\frac{x}{a}$
∫$\frac{1}{\sqrt{1-x^2}}$dx~∫$\frac{1}{\sqrt{1-co{s}^{2}x}}$dx

定积分

平均值

定积分是顶部不均匀图形的面积，该图形左、右、底部都是直线，让该面积除以区间即函数的平均值

积分上限函数

定义域由被积函数f(t)确定，与积分上下限无关

不定积分是f(x)的全体原函数
积分上限函数本质是f(x)的一个原函数，C由常数下限a决定，a为0时${\int }_a^x$f(t)dt就是C为0的f(x)的原函数；
而不定积分的C是任意常数。
所以，若${\int }_a^x$f(t)dt的a任意，则${\int }_a^x$f(t)dt就是不定积分

变上限积分求导特殊题型
被积函数f(t)不能含有x，用换元法将x换到f()外当做常数

定积分换元

被积函数f(x)在区间连续才能使用换元

定积分计算

周期性：

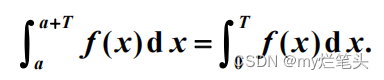
分部积分：
∫udv的u、v应都可积，即都连续
如tanx不可做u、v

定积分应用

旋转体体积

极坐标面积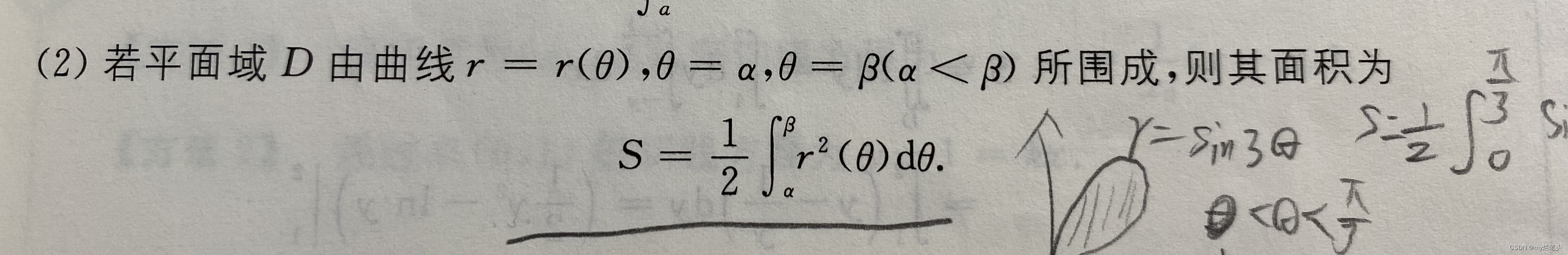

物理应用

形心：2013

微分方程

常识

不定积分是lnx不加绝对符

C可以是lnC

一阶常系数一定按一阶线性方程，不要按高阶非齐次算

可降阶微分方程

y’‘=f(y,y’)

令p=y’，则y’'=p$\frac{dp}{dy}$，化成自变量y因变量p的一阶微分方程，然后以可分离变量方程计算∫dp=∫dy
20年21题

一阶线性微分方程

y’+p(x)y=q(x) 其中q(x)是0时，中括号里俩C合成一个C

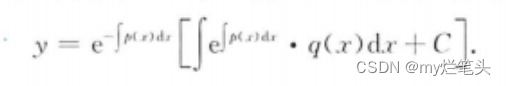
常系数非齐次线性微分方程

非齐次特解x^kQ_m(x)e^λx其实是将齐次通解的C置0的特解，其实是唯一的

多元函数微分

偏导

二阶偏导连续=>f’‘₁₂=f’'₂₁

求f(x,y)在(0,0)对x偏导数，让y为0，x逼近0

全微分

可微充分条件：一阶偏导且连续

极值

条件极值

真题：2013年

二重积分

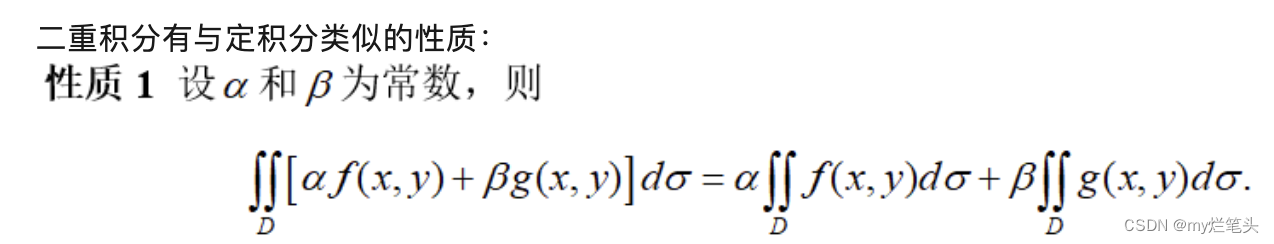
反过来D1+D2=D，前提是D1、D2的被积函数相同，这样D1、D2视作同一积分域，便于运用二重积分奇偶性计算

线性代数

行列式

不用按行/列展开，每项取不同行不同列元素乘积再乘（-1）的逆序
逆序是不按从小到大的一对数的对数

矩阵

初等变换

只能一行加另一行，不能一行自加一个数

矩阵运算

当A²-B²其中有一个是单位矩阵的时候，可以用平方差公式：
A²-E=(A+E)(A-E)
E-A²=(E+A)(E-A)

矩阵乘法

矩阵乘法无消去律，即AC=BC$/⟹$A=B；若C可逆，可用两边右乘C^-1消去C

(AB)C=A(BC)但不可(AC)B

矩阵行列式

|A^-1|=|A|^-1
|kAB|=kⁿ|A||B|
A=B$⟹$|A|=|B|
|Aⁿ|=|A|ⁿ

伴随矩阵

A^*A=AA^*=|A|E
(AB)^*=B^*A^*

AA^*=A^*A=|A|E $⟹$ A^*=|A|A^-1（前提A可逆）

初等矩阵

初等矩阵的逆矩阵是本身：E(i,j)^-1=E(i,j)

逆矩阵

AA^-1=E

向量

秩满可逆不为零	无关唯一只零解
方阵满秩	方阵不满秩
方阵可逆	方阵不可逆
方阵的行列式不为零	方阵的行列式为零
组成方阵的各个列向量线性无关	组成方阵的各个列向量线性相关
齐次方程只有零解（唯一解）	齐次方程有非零解（有无穷多解）

满足以上任意一条，则其他同列条件也同时满足

向量组

向量组等价 充分必要：r(A)=r(B)=r(A|B)
(矩阵等价 为r(A)=r(B))

线性相关 线性无关

r(A)=n线性相关
r(A)<n线性无关
b₁与a₁，a₂，a₃线性无关，b₂与a₁，a₂，a₃线性相关，则b₁+b₁与a₁，a₂，a₃线性无关

低维线性无关，则高维也线性无关

矩阵的秩

A是m×n矩阵，r(A)$\le$min(m，n)

若A可逆，则r(AB)=r(B)
[a₁x₁₁+a₂x₂₁,a₁x₁₂+a₂x₂₂]=[a₁,a₂]$$\left[\begin{array}{cc}x11& x12\\ x21& x22\end{array}\right]$$
r(AB)$\le$r(A)
r(AB)$\le$r(B)

向量组

向量组A能被向量组B线性表示$⟹$r(A)$\le$r(B)
向量组B(b₁,b₂,…b_n) $⟹$r(B)$\le$n

AB=C 得C的列向量组能被A的列向量组线性表示；C的行向量组能被B的行向量组线性表示；

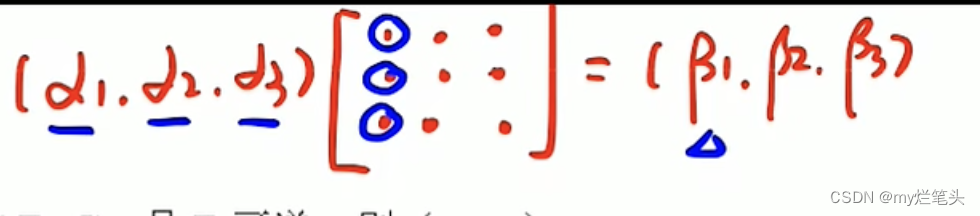
线性方程组

AB=0

非齐次

Ax=b有非零解（唯一解或无数解）<=>|A|=0

特征值特征向量

因|A|=λ₁λ₂λ₃，所以A可逆=>|A|$\ne$ 0 => A无0特征值

λ₁的特征向量为a₁，a₂，其线性组合a₃=k₁a₁+k₂a₂仍是λ₁的特征向量

矩阵相似

证明一个一般矩阵和一个一般矩阵相似：在三阶情况下，相同特征值的λ_iE-A的秩相同

两实对称矩阵A、B相似<=>特征多项式相等 即|λE-A|=|λE-B|

二次型

x=Qy =>y=Q^-1x
只有A经过可逆线性变换才能使惯性指数保持不变

规范型

根据惯性指数直接得，如正惯1，负惯1，则规范型为y₁²+y₂²

合同

1、实对称矩阵A相似于矩阵B，相似一定合同，但合同不一定相似
2、A合同B等<=>A、B正负惯相等
3、A合同B，则|A|与|B|同号
证明：Q^TAQ=B =>
|Q^TAQ|=|B| =>
|Q^T||A||Q|=|B|=>(|Q^T|=|Q|)
|Q|²|A|=|B|
因|Q|²>0则|A|同号|B|