一 概念
多重共线性: 也即使用的多个预测变量之间存在线性相关。多重共线性会导致解的不稳定,进而可能导致意外的结果。在线性代数中,基坐标必须是相互正交的,也即不相关的,此处在做多元回归预测时,必须保证预测变量之间是不相关的。
避免手段:
(1)分析之前:
a. 逐个计算预测变量之间的相关系数。
> cor(sugar$sugars,sugar$shelf)
[1] 0.1004379
> cor(sugar$fiber,sugar$potass)
[1] 0.9033737b.为预测变量建立矩阵图
> #同时画多个变量的对照图需要使用 car包中的 scatterplotMatrix函数
>install.packages("car")
>library(car)
>#使用谷物数据集的 “糖”,“纤维”,“钾”三列数据
> sugar_frame<-as.data.frame(sugar[,c("糖","纤维","钾")])
>#画出对照图
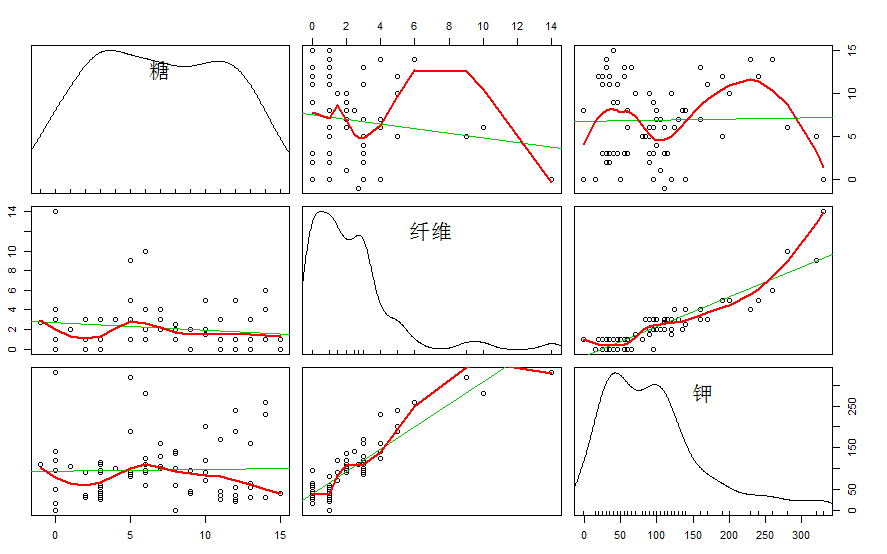
> scatterplotMatrix(sugar_frame,spread=F,lty.smooth=2,var.labels=c("糖","纤维","钾"))结果如下图:
可以看到第四张和第六张是纤维和钾的相关图,可以看出他们之间有很强相关性。
(2)分析之后:方差膨胀因子(variance inflation factors,VIFs)
其中Ri^2表示R^2的值是通过在其他预测变量上回归分析xi得到的。假设xi和其他变量没有任何关系,那么Ri^2=0,于是可以得到VIFi=1/(1-0)=1。也即VIF最小值为1,没有最大值.
VIFi的变化对第i个系数的变化率Sbi如何产生影响,有如下公式:
如果xi与其他预测变量不想管,那么VIFi=1,而且相关系数的标准差Sbi没有增大。然而如果xi与其他变量相关,那么较大的VIFi值会使得相关系数的标准差Sbi过度膨胀。因此,方差估计的膨胀会导致估计精度的下降。粗略的经验法则如下:
VIF>=5 模型有中度的多重共线性(相当于R^2=0.08)
VIF>=10 模型中有严重多重共线性(相当于R^2=0.90)
下面来查看谷物数据集中 糖、纤维、钾的膨胀因子
> #回归拟合
> fit<-lm(data=sugar,rating~sugars+fiber+potass)
>#注意,我们只是用了sugar数据集中包含“糖”,“纤维”,“钾”三列数据的sugar_frame
>#进行膨胀因子计算时,需要使用gvlma包中的vif函数,因此需要先安装
> install.packages("gvlma")
> library(gvlma)
Warning message:
程辑包‘gvlma’是用R版本3.0.2 来建造的
>#线性模型的综合验证
> gvlma(fit)
Call:
lm(formula = rating ~ sugars + fiber + potass, data = sugar)
Coefficients:
(Intercept) sugars fiber potass
52.6762 -2.0510 4.3701 -0.0543
ASSESSMENT OF THE LINEAR MODEL ASSUMPTIONS
USING THE GLOBAL TEST ON 4 DEGREES-OF-FREEDOM:
Level of Significance = 0.05
Call:
gvlma(x = fit)
Value p-value Decision
Global Stat 7.24415 0.12353 Assumptions acceptable.
Skewness 5.61716 0.01779 Assumptions NOT satisfied!
Kurtosis 0.02125 0.88411 Assumptions acceptable.
Link Function 0.40164 0.52624 Assumptions acceptable.
Heteroscedasticity 1.20410 0.27250 Assumptions acceptable.
>#查看膨胀因子 vif
> vif(fit)
sugars fiber potass
1.164237 6.327286 6.204047
二. 变量选择方法
2.1 向前选择程序
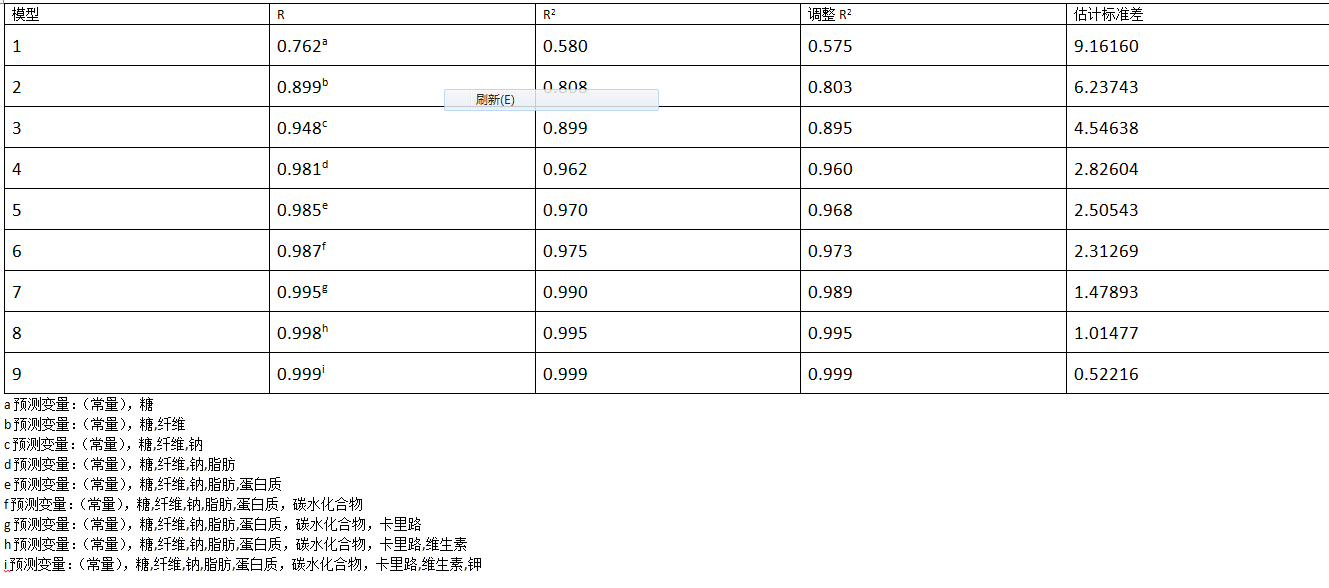
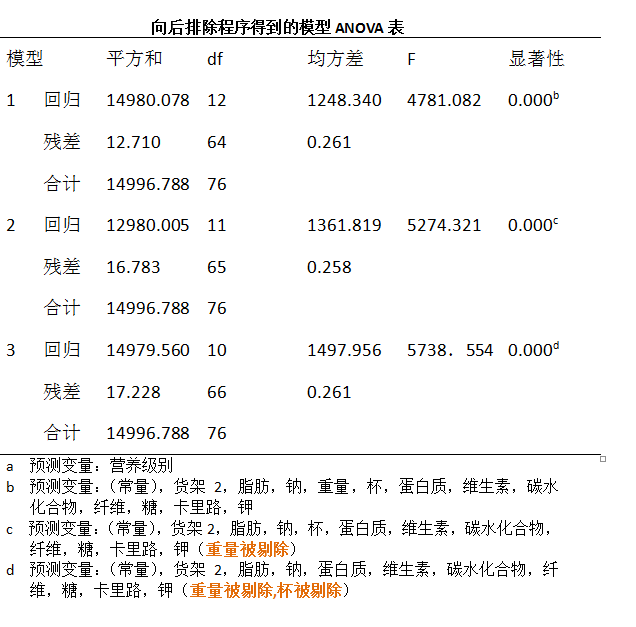
2.3 逐步选择程序
2.4 最优子集程序
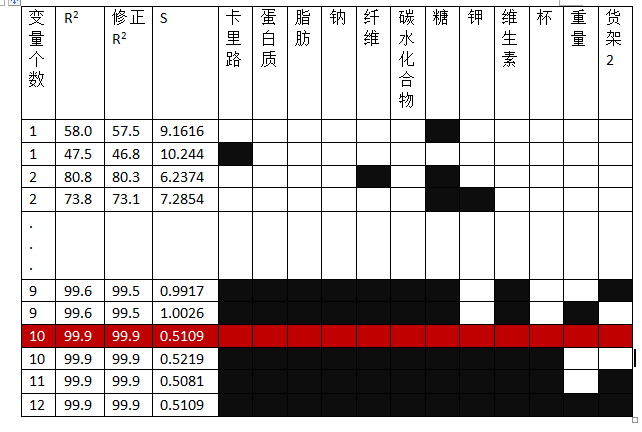










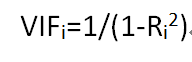


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








