机器学习总结7_从模型融合到Adaboost

0.

从模型融合开始说起。
有时候我们会想到这么一个问题：我们能不能把几个模型融合在一起达到更好的效果呢？当然可以了。
假设现在有$g_1,g_2,..g_n$,这n个模型，将这n个模型融合起来的基本策略大概有这么几种：

1、从这n个模型中，选出来一个误差最小的。
2、将每个模型都同等对待。

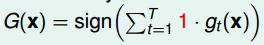
3、给每个模型不同的权重。(通过线性回归求解各个权重)

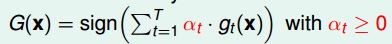
4、并不是一定要是线性的，可以使用其他的非线性的算法，进行非线性的模型融合。

说明：
关于2、下面证明了G(X)的误差比随机挑一个模型g的误差小。
注意：因为我们并不知道随机挑的是哪一个g，所以这里用所有模型的误差的平均，和G的误差进行比较。

关于3、 实际上就是把这n个模型当做n个特征，进行线性回归，就求出相对应的权重了。
有时候通过模型融合可以达到 feature-transform或者regularization的效果。
现在又有个问题了，如何求出来那么多不一样的$g_i$啊？

这上面简单列举了四种产生不同g的方法，除了这些之外，统计学中还有种方法bootstrapping。

bootstrapping方法的实现很简单，假设你抽取的样本大小为n，在原样本中有放回的抽样，抽取n次。这样就产生了一个新的训练集，同样进行类似的过程，就可以产生另外一个新的训练集。在不同的训练集上进行模型的训练就可以得到不同的g。

1. Adaboost

上面这些都是先得到各种不同的模型$g_i$,然后再通过不同的策略进行融合。可不可以在求出来一个模型的同时，求得相应的权重呢？当然是可以的，Adaboost就是这么做的。
在开始介绍Adaboost之前，先插入点其他的东西。
在上面介绍了bootstrapping，现在将bootstrapping抽象表示：

这是一个具体的例子，在数据集D进行4次有放回抽样，得到一个新的数据集。我们在这里用向量u表示某个具体的样本被抽中的次数(如图中所示)，在误差前乘以对应的u就可以求得模型g了。每进行这么一轮抽样，产生不同的向量u，就代表这不同的数据集，从而就可以得到很多不同的模型g了。

下面开始正式介绍Adaboost。Adaboost 和bootstrapping有点类似，用不同的u生成不同的模型g。有一点不一样的是，Adaboost中的u不是随机抽样得到的，是根据前一个$u^{(t-1)}$调节得到的。

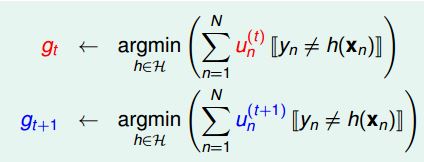
在模型融合中，我们希望各个$g_1...g_n$的模型都尽可能不一样。
上面是先后求得的两个模型，$u^{(t+1)}$如何根据$u^{t}$进行调整，才能使得$g_t和g_{t-1}$尽可能不一样呢？答案是：给予在$g_t$犯错的样本更大的权重。

使得犯错的和做对的概率一样(和随机猜的效果一样)。这样产生的新模型$g^{(t+1)}$和$g^{(t)}$就会很不一样。
具体的调整如下所示：

如果对这里有疑问的话，建议自己顺着这个思路具体的算一下，你会发现通过这么调整：会使得调整之后的数据对$g^{(t)}$而言，做错的和做对的概率是一样的(都是0.5)。

这么调整的物理意义是：增大前一个模型$g^{(t)}$做错的样本的权重，减小前一个模型$g^{(t)}$最对的样本的权值，让接下来的模型$g^{(t+1)}$着重处理前面做错的那些样本。

每个模型的权重是通过如下确定的：


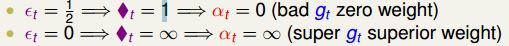
说明：ln()函数是单调递增的
(1)、当这个模型的错误率是0.5时(也就是这个模型和乱猜的效果差不多时)，那这个模型的权重就是0，那这个模型对最后的结果不起作用。
(2)、当这个模型的错误率是0时，那这个模型的权重就是无限大。
这个模型的错误率越小，那这个模型的权重越大。

！上面总共出现了两个权重，一个是样本的权重u，另一个是模型的权重a！！注意区分！！！

算法总流程如下：

2.

又到了分析$E_{in}和E_{out}$的时候了。

有关于$E_{in}$这个的证明：
只要每一个的模型g的效果比乱猜好一点的话(犯错率比0.5小的话)， 在T=O(logN)次迭代之后，Adaboost的$E_{in}$就会为0。这也就是说明在Adaboost在很短的时间内，就会使$E_{in}$就会为0。
关于$E_{out}和E_{in}$的关系，通过VC维，也就是上图中的式子。
T=O(logN)是很小的，当N足够大时，$E_{out}和E_{in}$就会很接近，保证了这个算法的泛化能力，避免了overfitting。

3.

可能你还会对此有疑问，强烈推荐台湾大学的《机器学习技法》的第七讲和第八讲，对上面的问题讲述的非常清楚。