加权最小二乘法

最小二乘法是对参数估计的一种算法，其优点是不需要系统的先验知识，所以是一种系统辨识很重要的算法。下面对其进行简单的介绍：

• 一般最小二乘法

这里假设状态x为n*1维的列向量，而测量值为状态x的线性组合，假设进行了L次观测，则局部观测模型有：

利用所有的观测信息合成观测模型则有：

其中有：

根据上述模型，给出最小二乘的极小化性能指标：

对最小化性能指标J求偏导，可得：

则有一般最小二乘估计，这样估计的误差均方差阵为：

• 加权最小二乘法

在没有测量值误差的统计信息时，采用一般最小二乘法，但是一般最小二乘法没有考虑两种测量仪器测量精度不同的特点，如果在已知测量值误差统计信息时，我们就可以采用加权最小二乘法，进一步提高状态估计精度。

加权最小二乘法与一般最小二乘法不同的地方是最小化性能指标发生改变，加入了权重矩阵，这里我们选择让测量精度高的数据权重值大一些，而测量精度低的数据权重值小些，构成如下最小化性能指标：

其中权重矩阵为：

对最小化指标求偏导可得：

同理求误差方差阵如下：

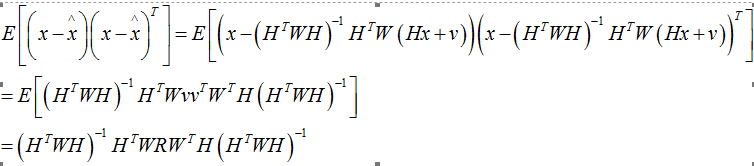
可以证明估计后状态误差小于每个传感器的误差。