使用python进行排放清单不确定性分析（蒙特卡洛模拟）

王德芙捏

已于 2023-06-15 10:49:40 修改

阅读量3.8k

点赞数 7

文章标签： python

于 2023-06-15 10:49:25 首次发布

本文链接：https://blog.csdn.net/hy19990903/article/details/122099415

版权

目前能够进行蒙特卡洛模拟的软件有很多，如crystal ball、AUVtoolpro等，在排放清单数据较为简单，源类较少的情况下使用以上软件来操做是极为方便的，但是当排放b清单原分类较为繁杂，数据的前期处理就变得异常繁琐，充斥着大量的重复工作。使用python或者其他语言来进行编程分析可以降低前期数据处理的难度，减少无意义的重复劳动。

如果各位有不明白的地方可以添加好友询问，vx：wonderful11451

一、引入库包

笔者使用的库包为数据处理中较为常用的pandas以及numpy，pandas主要用来进行数据的读取、写入以及统计等工作，numpy则主要进行蒙特卡洛模拟中的随机抽样工作。

import pandas as pd
import numpy as np

二、读取清单文件

清单文件的格式需要包括活动水平、sigma1（活动水平概率分布第二参数）、sigma2（排放因子活动水平第二参数）、排放源类、污染物排放因子以及污染物去除效率，以工业锅炉排放源为例，具体格式见下图：

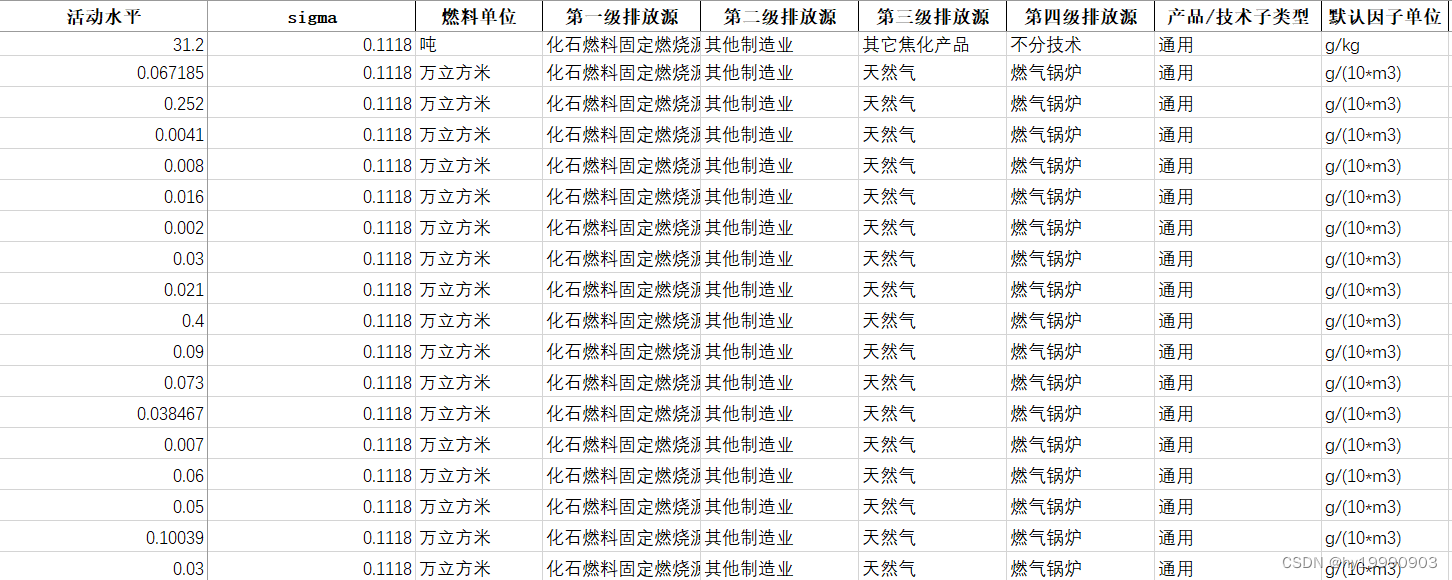
file = r"清单数据.xlsx"

三、定义模拟函数

函数设置如下：

def uncert_excel(file, spc):
    xlsx = r"2021_"+spc+".xlsx"
    xlsx2 = pd.ExcelWriter(xlsx)
    ll2 = pd.DataFrame()
    for i in range(41):     
##41为excel表格中的sheet数量，根据个人需要自行输入。

##获取sheet名称
        df = pd.read_excel(file, sheet_name=i)
        df2 = pd.read_excel(file, sheet_name=None)
        df = df[df['活动水平'] != 0]
        df = df.reset_index()
        print(i)
        name_yuanlei = list(df2.keys())[i]
        print(name_yuanlei)
  
        ll = pd.DataFrame()

##根据条件筛选需要的数据
        if spc + '排放因子' in df.columns:
            dfSO2 = df[df[spc + '排放因子'] != 0]
            dfSO2 = dfSO2.reset_index()
##删除排放因子为0的行


            if spc + '去除效率' in dfSO2.columns:
                a = dfSO2['活动水平'] * (1 - dfSO2[spc + '去除效率'] / 100)
                dfSO2.insert(0, spc, a)
##计算活动水平*（1-去除效率），此处笔者的文件去除效率为小于100的数值，所以需要除100，此处根据个人需要调整。


            else:
                a = dfSO2['活动水平']
                dfSO2.insert(0, spc, a)
##有些源类不存在去除效率，如果没有去除效率这一栏，则跳过上述计算步骤


            for j in range(len(dfSO2[spc])):
                number = dfSO2[spc][j]
                ef = dfSO2[spc + '排放因子'][j]
                sigma_q = dfSO2['sigma1'][j]
                sigma_ef = dfSO2['sigma2'][j]
                number2 = np.log(number)
                ef2 = np.log(ef)
                a = np.random.lognormal(mean=number2, sigma=sigma_q, size=10000)
                b = np.random.lognormal(mean=ef2, sigma=sigma_ef, size=10000)
##根据输入的活动水平、排放因子与对应的sigma1、sigma2进行10000次抽样

                c = a * b
##计算最终排放量


                s_type = dfSO2['第一级排放源'][j] + dfSO2['第二级排放源'][j] + dfSO2['第三级排放源'][j] + dfSO2['第四级排放源'][j] + dfSO2['产品/技术子类型'][j]
                ll[str(j)] = pd.DataFrame(c)
                # name = dfSO2['一级排放源'][j]+dfSO2['二级排放源'][j]+dfSO2['三级排放源'][j]+dfSO2['四级排放源'][j]+dfSO2['产品/技术子类型'][j]
                ll2[name_yuanlei] = ll.apply(lambda x: x.sum(), axis=1)
    ll2[spc + '_all'] = ll2.apply(lambda x: x.sum(), axis=1)
    a = ll2[spc+"_all"]
    b = a.quantile([0.025,0.975])
##计算结果的95%置信度下的数据，并把保存至excel文件


    b.to_excel(xlsx2, sheet_name='分位数据')
    ll2.to_excel(xlsx2, sheet_name='ALL_sum',index=None)
    xlsx2.save()
    xlsx2.close()

四、全部代码及输出结果

import pandas as pd
import numpy as np

file = r"清单数据.xlsx"

def uncert_excel(file, spc):
    xlsx = r"2021_"+spc+".xlsx"
    xlsx2 = pd.ExcelWriter(xlsx)
    ll2 = pd.DataFrame()
    for i in range(41):     
##41为excel表格中的sheet数量，根据个人需要自行输入。

##获取sheet名称
        df = pd.read_excel(file, sheet_name=i)
        df2 = pd.read_excel(file, sheet_name=None)
        df = df[df['活动水平'] != 0]
        df = df.reset_index()
        print(i)
        name_yuanlei = list(df2.keys())[i]
        print(name_yuanlei)
  
        ll = pd.DataFrame()

##根据条件筛选需要的数据
        if spc + '排放因子' in df.columns:
            dfSO2 = df[df[spc + '排放因子'] != 0]
            dfSO2 = dfSO2.reset_index()
##删除排放因子为0的行


            if spc + '去除效率' in dfSO2.columns:
                a = dfSO2['活动水平'] * (1 - dfSO2[spc + '去除效率'] / 100)
                dfSO2.insert(0, spc, a)
##计算活动水平*（1-去除效率），此处笔者的文件去除效率为小于100的数值，所以需要除100，此处根据个人需要调整。


            else:
                a = dfSO2['活动水平']
                dfSO2.insert(0, spc, a)
##有些源类不存在去除效率，如果没有去除效率这一栏，则跳过上述计算步骤


            for j in range(len(dfSO2[spc])):
                number = dfSO2[spc][j]
                ef = dfSO2[spc + '排放因子'][j]
                sigma_q = dfSO2['sigma1'][j]
                sigma_ef = dfSO2['sigma2'][j]
                number2 = np.log(number)
                ef2 = np.log(ef)
                a = np.random.lognormal(mean=number2, sigma=sigma_q, size=10000)
                b = np.random.lognormal(mean=ef2, sigma=sigma_ef, size=10000)
##根据输入的活动水平、排放因子与对应的sigma1、sigma2进行10000次抽样

                c = a * b
##计算最终排放量


                s_type = dfSO2['第一级排放源'][j] + dfSO2['第二级排放源'][j] + dfSO2['第三级排放源'][j] + dfSO2['第四级排放源'][j] + dfSO2['产品/技术子类型'][j]
                ll[str(j)] = pd.DataFrame(c)
                # name = dfSO2['一级排放源'][j]+dfSO2['二级排放源'][j]+dfSO2['三级排放源'][j]+dfSO2['四级排放源'][j]+dfSO2['产品/技术子类型'][j]
                ll2[name_yuanlei] = ll.apply(lambda x: x.sum(), axis=1)
    ll2[spc + '_all'] = ll2.apply(lambda x: x.sum(), axis=1)
    a = ll2[spc+"_all"]
    b = a.quantile([0.025,0.975])
##计算结果的95%置信度下的数据，并把保存至excel文件


    b.to_excel(xlsx2, sheet_name='分位数据')
    ll2.to_excel(xlsx2, sheet_name='ALL_sum',index=None)
    xlsx2.save()
    xlsx2.close()

Al = ['SO2','NOx','CO','VOC','NH3','PM2.5','PMcorase','BC','OC']
for spc in Al:
    uncert_excel(file,spc)

表格中包括抽样数据以及用于计算不确定性的排放量数据。