求证:∠A + ∠B + ∠C + ∠D + ∠E = 180
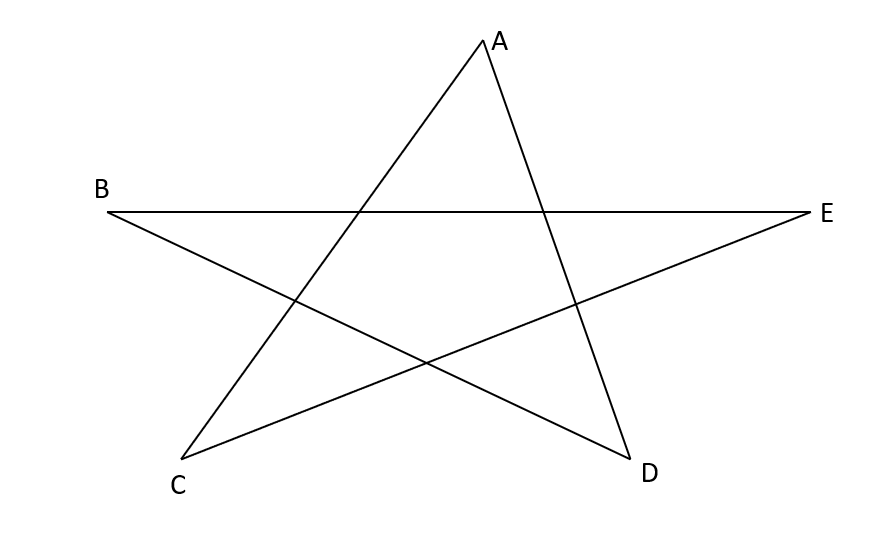
证明:做辅助线,连接 AE.

∵ △AEC 内角和为 180度
∴ ∠C + ∠CAD + ∠DAE + ∠AEB + ∠E = 180 (1)
∵ △BOD 内角和为 180度,
∴ ∠B + ∠D + ∠BOD = 180 (2)
∵ △AOE 内角和为 180度,
∴ ∠AOE + ∠DAE + ∠AEB = 180 (3)
其中 ∠BOD 与 ∠AOE 为对顶角,∴ ∠BOD = ∠AOE
令 (1) + (2) - (3),得 ∠A + ∠B + ∠C + ∠D + ∠E = 180


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










