堆叠体体积求值的范围问题：已知堆叠体三视图，求该堆叠体体积的最大值和最小值

题目：求这个堆叠体的体积最大值和最小值。

理论依据仍然是使用俯视图标注法，即笔者这篇文章介绍的详细步骤：

https://zhuanlan.zhihu.com/p/602290167

注：能够正确反映物体长、宽、高尺寸的正投影工程图（主视图，俯视图，左视图三个基本视图）为三视图，这是工程界一种对物体几何形状约定俗成的抽象表达方式。

之所以有最大值和最小值，说明俯视图有些位置的立方体个数无法唯一确定。

从数字1 开始突破：

左边：横着看过去都是1
下面：竖着看过去都是1

(1) 第三列一定能够确定，标 1, 如下图黄色所示。因为如果标2，就会与主视图里的 1 矛盾了，故只能标1.

浅绿色的3，代表从左往右看看到3的高度，说明粉红色两个位置一定有一个位置为3.

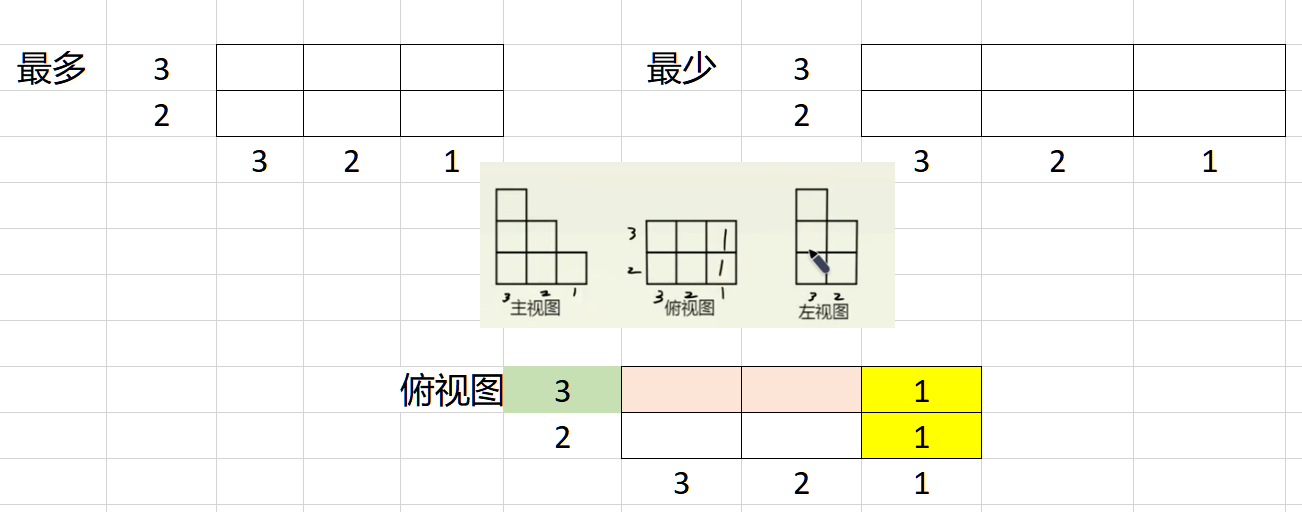
第一个粉红色位置可以确定为3，因为如果第二个粉红色位置为3，就会和主视图中第二列的2矛盾。

红色区域如果填3，就会和左视图第二列的2相矛盾。

所以最后能够确认的三个位置如黄色区域所示：

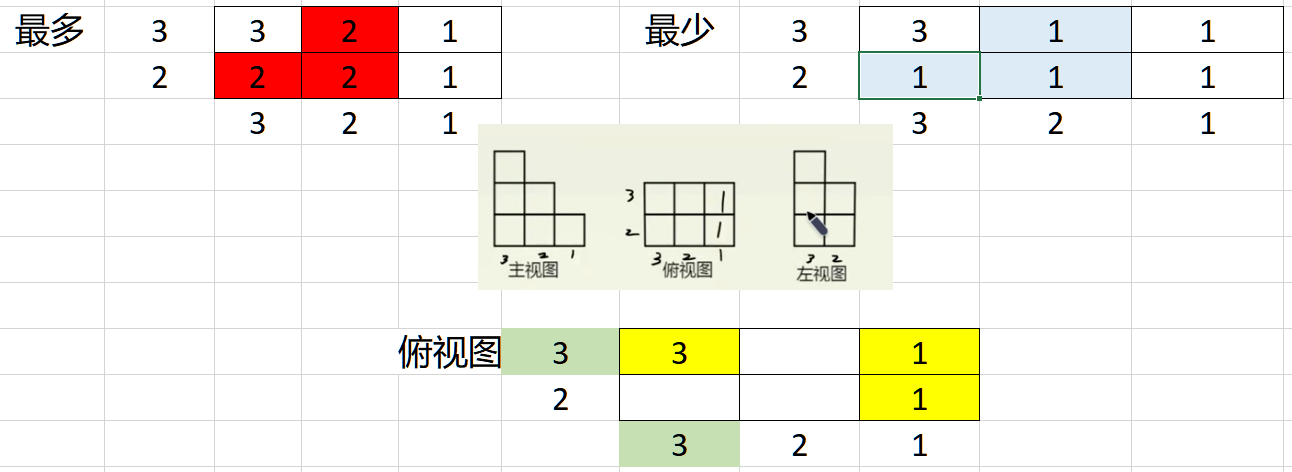
体积最大：空行不能随便填，尽可能多，但是不能超过行和列的限制。

答案见下图红色：

体积最小：上图灰色是错误的。因为和主视图和左视图矛盾了。

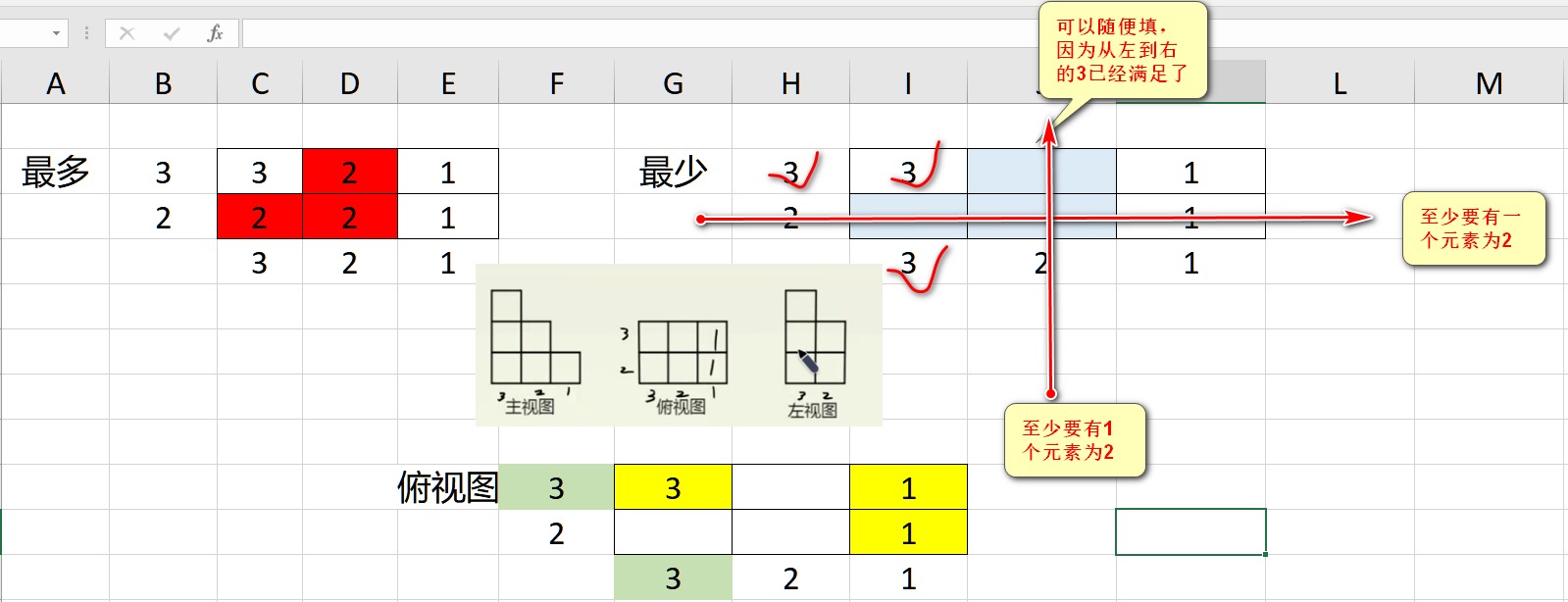
故能确定出绿色区域为2，其他区域填1即可做到体积最小。

解题步骤总结

1. 把能够唯一确定的先标注出来
2. 体积最大：让其他位置尽可能多，但不能违反其他两种视图的约束
3. 体积最小：行列相同数交叉位置一次性满足