【计算机视觉|人脸建模】3D人脸重建基础知识（入门）

本系列博文为深度学习/计算机视觉论文笔记，转载请注明出处

一、三维重建基础

三维重建（3D Reconstruction）是指根据单视图或者多视图的图像重建三维信息的过程。

1. 常见三维重建技术

	人工几何模型	仪器采集	基于图像的建模
描述	基于几何建模软件通过人机交互生成物体三维几何模型	基于结构光和激光扫描技术的三维成像仪	通过单张或者多张二维图像来恢复图像或场景的三维结构
优点	精度高	精度高（毫米）、真实的物体三维数据	成本低廉
缺点	需要专业人士，人力和时间成本高	仪器成本高，难以大规模采集	难度大，复杂
示例	3DMax、Blender（提供api接口，可编程开发）	通常用来构建3D数据库（数据集）	从一个人脸模型开始，进行形状的拟合、变形、纹理贴图

2. 人脸三维重建的特点和难点

从二维图像重建真实的人脸三维形状和纹理是一个病态问题（ill-posed problem）

2.1 特点

• 人脸图像预处理技术很多

  • 人脸检测、特征点定位、人脸对齐与分割等

• 人脸共性大，且有明确的相对位置关系

  • 人脸重建问题转化为个性化的人脸模型的参数估计

2.2 难点

• 人脸生理结构和几何形状非常复杂

  • 使用现有数学曲面容易得到过于光滑的结果

  • 使用点云数据三角化建立的曲面比较粗糙

• 明显的特征点较少，低纹理地区、亮度变化平滑、梯度信息少

  • 难以产生可靠的三维点云数据

3. 人脸三维重建基础技术

人脸特征分为几何特征和纹理特征，建模需要同时回复这两部分信息。

3.1 几何建模

1. 多边形网格建模技术（主流）

   • 一个网络模型由若干三维网格点Vertex和网格点围成的多边形面片Facet组成，网格点和面片数量越多，模型真实感越强。

     • 下图是四边形网格的示例

       

     • 下图是三角形网格的示例

       

   • 在网络上选取控制点，移动控制点完成网络的形变。

     • 均匀网络（不常用）

     • 非均匀网络：突出面部细节，如眼睛嘴唇等处密度更大。而脸颊等处密度较小，可减小复杂度。

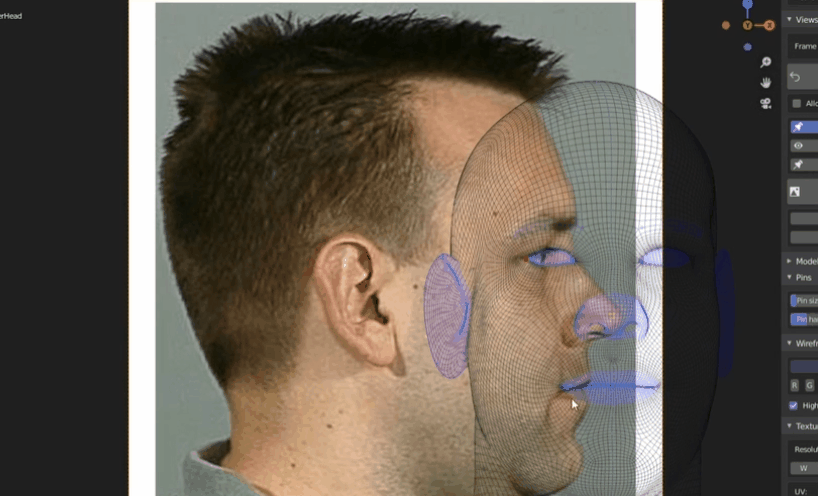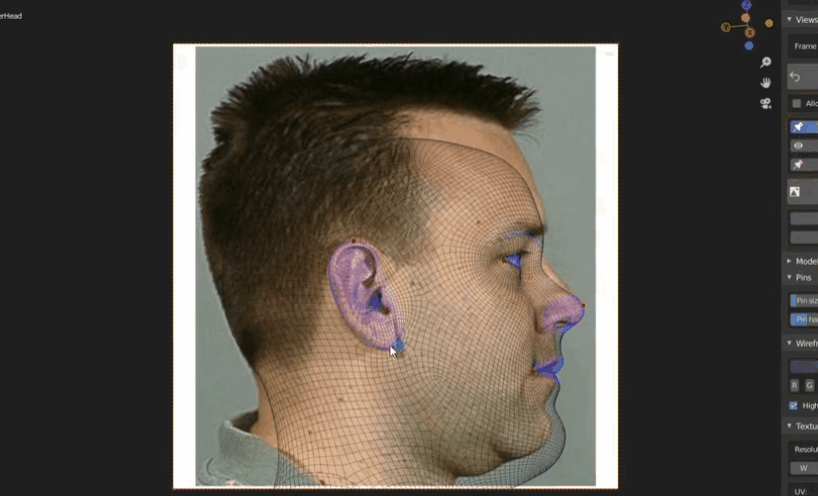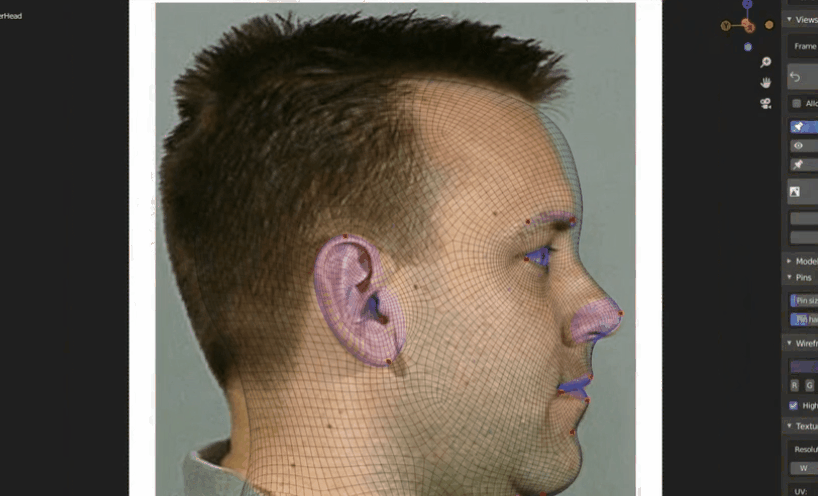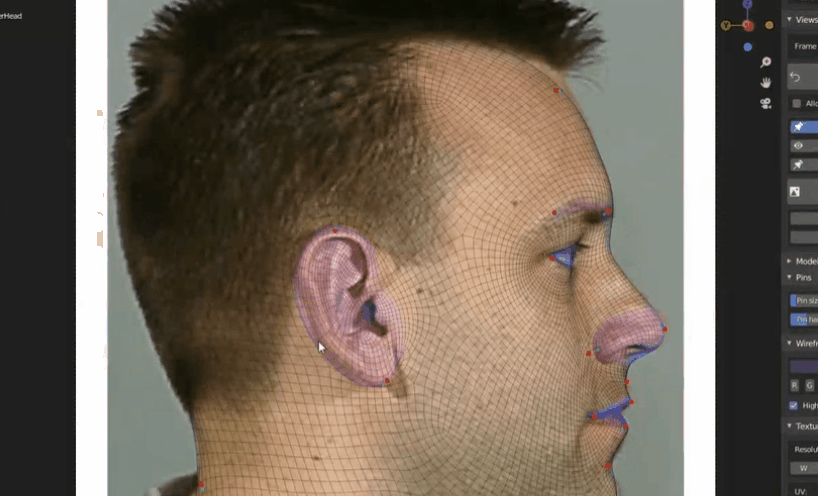
2. 曲面建模技术（不常用）

3.2 纹理映射

Basel人脸库（Basel Face Model，Basel面部模型，BFM模型）中三维模型中的任意一个点可以用(x,y,z,r,g,b)表示，其中x,y,z为位置坐标，r,g,b是颜色坐标，也可以称之为纹理。

Basel面部模型，这是一个3D人脸形状模型，以及可能相关的肤色和纹理模型。这个模型基于大量的3D扫描和颜色图像来建立，是面部形状和纹理变异的统计模型，可以用于计算机视觉和图形的各种应用，如面部识别、动画和特效。目前有三个版本的数据集（2009、2017和2019）。

纹理映射（Texture Mapping）也称纹理贴图，简单来说就是将二维图像贴到三维图像的表面，一般需要和光照模型、图像融合等技术结合。也常采用高分辨率的二维纹理图（如下）对三维的纹理进行表征。关于BFM模型和3DMM技术，后文会有更详细的说明。

具体来说，就是重建好三维模型之后，将三维的模型往二维图像中进行投影，采样到像素值之后再赋值给三维网络。

截至21年，最新的技术是使用深度学习进行渲染，如neural rendering方法。

相关技术链接：

• BFM模型介绍及可视化实现（C++） - Bemfoo - 博客园 (cnblogs.com)
• 神经渲染（neural rendering） - 知乎 (zhihu.com)

二、传统三维人脸重建技术

• 基于多目立体视觉匹配的方法
• 3DMM拟合
• shape from shading
• structure from motion

本节重点介绍前两者。

1. 多目立体视觉匹配

多目立体视觉（Multiple View Stereo，MVS）

1.1 标系与摄像机标定

三维物体成像，需了解以下四个坐标系。图文符号略有不符，请以文为主。

1. 世界坐标系，world

   • 真实世界的立体空间坐标，坐标轴（X_w，Y_w，Z_w），单位是米

2. 相机坐标系，camera

   • 根据透镜成像原理，将世界坐标系在照相机内呈现的三维坐标系，坐标轴（X_C，Y_C，Z_C），单位是米

   • 从世界坐标系到相机坐标系，需要经过比例缩放、平移旋转等刚体变化

   • 从世界坐标系到相机坐标系，经历转换公式：

     $$\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]=\left[\begin{array}{ccc}{r}_{00}& r_{01}& r_{02}\\ r_{10}& r_{11}& r_{12}\\ r_{20}& r_{21}& r_{22}\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\end{array}\right]+\left[\begin{array}{c}{T}_x\\ T_y\\ T_z\end{array}\right]$$

     • 其中，$\left[\begin{array}{ccc}{r}_{00}& r_{01}& r_{02}\\ r_{10}& r_{11}& r_{12}\\ r_{20}& r_{21}& r_{22}\end{array}\right]$是旋转矩阵，$\left[\begin{array}{c}{T}_x\\ T_y\\ T_z\end{array}\right]$是平移矩阵
     • 他们与摄像机无关，所以这两个参数称为摄像机的外参（Extrinsic Parameter）

3. 图像坐标系，image

   • 将相机呈现的三维坐标投影到二维的平面，原点为成像平面的中心点，坐标轴（X，Y），单位是毫米

   • 从相机坐标系到图像坐标系的透视投影（Perspective Projection）基于小孔成像原理，其在成像平面上的投影点的坐标利用简单的相似三角形比例关系求出，如公式：

     $$\{\begin{array}{l}x=\frac{f{x}_c}{Z_c}\\ y=\frac{f{y}_c}{Z_c}\end{array}$$

     • f是摄像机的焦距，属于摄像机的内参（Intrinsic Parameter）

4. 图像（像素坐标系），pixel

   • 从图像坐标系离散采样得到的图像，是一个二维的坐标系，原点位于左上角，坐标轴为（U，V），单位是像素

   • 此步骤主要是进行离散化，参考公式：

     $$\{\begin{array}{l}u=\frac{x}{dx}+u_0\\ v=\frac{y}{dy}+v_0\end{array}$$

综合以上信息，总的变化过程为

$$Z_c\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}\frac{1}{dx}& 0& u_0\\ 0& \frac{1}{dy}& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}f& 0& 0& 0\\ 0& f& 0& 0\\ 0& 0& 1& 0\end{array}\right]\left[\begin{array}{cccc}{r}_{00}& r_{01}& r_{02}& T_x\\ r_{10}& r_{11}& r_{12}& T_y\\ r_{20}& r_{21}& r_{22}& T_z\\ 0& 0& 1& 0\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]=P\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]$$
其中，

• $3\times 4$的矩阵$P$又称为摄像机模型（Camera Model）

• $$\left[\begin{array}{ccc}\frac{1}{dx}& 0& u_0\\ 0& \frac{1}{dy}& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}f& 0& 0& 0\\ 0& f& 0& 0\\ 0& 0& 1& 0\end{array}\right]$$称为摄像机的内参矩阵，因为它仅由摄像机内部参数决定。

1.2 基于立体视觉匹配的重建原理

使用两张图像的立体视觉技术称为双目立体视觉，使用多张图像的立体视觉技术则被称为多目立体视觉。

通常包含以下重要步骤，以双目立体视觉匹配来举例说明：

1. 图像获取，获取两张图像，通常一左一右
2. 摄像机建模，即摄像机内参标定
3. 双目校正，基于每个相机的内参矩阵和相机的相对位置关系参数共同影响，对图像进行矫正变形，使校正后的图像成像点的坐标在同一水平线上
4. 特征提取，获取图像当中的显著特征点，当然也可以使用所有图像点
5. 图像匹配，关键一步，对两幅图像进行匹配，有两种方法：
   1. 特征匹配。建立稀疏图像特征点之间的对应关系，如SIFT特征点。
   2. 稠密匹配。为每个像素确定对应的匹配像素，建立稠密的视差图。
6. 视差图（深度图估计）
7. 内插

双面立体匹配原理：

空间中一点p投影在左相机图像坐标是$p_l(x,y)$，投影到右边相机图像坐标是$p_r(x^{\prime },y^{\prime })$，由于双目立体校正后的左右图像的成像点在相同的行上，所以$y=y^{\prime }$，根据三角形相似原理，有如下关系：

$$\frac{a}{Z}=\frac{a-(x-x^{\prime })}{Z-f}$$
所以深度$Z=\frac{af}{x-x^{\prime }}$，其中a表示两台相机的基线距离，f表示相机的焦距，x、x’表示两投影点的视差

相关技术链接：

• SIFT特征点 - 知乎 (zhihu.com)
• vision.middlebury.edu/stereo-对各立体匹配算法进行测评

1.3 基于立体视觉匹配的重建方法的特点

• 优势在于：提供稠密的视差信息，从而恢复稠密的三维点云，重建的三维人脸表面较为精细。

• 缺点在于：需要寻找匹配点，对于人脸图像来说，皮肤比较光滑，因此纹理信息较少，只能获得少量特征点，通常不超过200个。而立体视觉匹配需要对稠密点进行匹配，当被用作人脸图时，很多相似区域会产生比较高的匹配相应，产生很严重的二义性。另外，人脸图像中常见的光照变化与自遮挡产生的阴影也给立体视觉匹配产生很大困难。

因此该方法没有太大优势，而且计算量大，步骤复杂。

2. 3DMM

3DMM（3D Morphable Model）在1999年提出，它假设每一张三维人脸可以由一个数据集中的所有人脸组成的基向量空间表示，而求解任意三维人脸的模型，实际上等价于求解每个基向量的系数。对于一张人脸， 我们有如下的特征：

• 前额长度（变化幅度在[0,1]）

• 眼睛大小

• 鼻子大小

• ……

这些特征就是人脸基向量。

对于任意给定的一张2D人脸图片，其3D人脸可以由3DMM的一系列人脸基向量进行加权组合，其中 $M$表示基向量的数量（即数据集中人脸模型个数），${\alpha }_i$表示控制人脸形状（几何模型，Shape）的每个基向量的系数，${\beta }_i$表示控制人脸纹理（纹理映射，Texture）的基向量的系数

$$\{\begin{array}{l}{S}_{mod}=\sum _{i=1}^M{\alpha }_i{S}_i\\ T_{mod}=\sum _{i=1}^M{\beta }_i{T}_i\\ \sum _{i=1}^M{\alpha }_i=\sum _{i=1}^M{\beta }_i=1\end{array}$$
$S_i$、$T_i$就是数据集中的第$i$张人脸的形状向量和纹理向量。

2.1 BFM数据集

最早公布的数据集（2009）的平均人脸形状和人脸平均纹理，如图所示：

注意，人脸基向量是通过PCA（primary component analysis，主成分分析法）得到的相互正交（orthogonality）的基向量，这样的目的是使得基向量对3D人脸的影响相互独立，避免造成难以分析的人脸耦合问题。

图中，第一列的图是形状和纹理的平均值，从第二列到第四列中的两行，分别是对第1、2、3个主成分，+/-方差5所得的模型。

关于数据集：

每个模型由53490个点描述。每个模型还包括性别、脸部高度、年龄等标签；在2017和2019两个版本中，还提供了表情系数。为了更精确地重建，人脸还被分为4个区域，可以对每个区域进行更精确的重建，然后融合。

2.2 3DMM重建原理

根据前面所说的，任意一个点可以用(x,y,z,r,g,b)表示。

(x,y,z)称为形状向量，(r,g,b)称为纹理向量。前者决定脸的轮廓，后者决定脸的肤色。

因此每一张人脸可以表示为：

形状向量（Shape Vector）：$S=(X_1,Y_1,Z_1,\dots ,X_n,Y_n,Z_n)$

纹理向量（Texture Vector）：$T=(R_1,G_1,B_1,\dots ,R_n,G_n,B_n)$

其他公式参考上面写过的内容。

具体解释一下正交的部分：

在实际建模的过程中，不能直接使用$S_i$和$T_i$作为基向量，因为它们之间不是正交相关的，所以接下来需要使用PCA进行降维分解。

1. 计算$\overline{S}$和$\overline{T}$，即形状和纹理向量的平均值。

2. 中心化人脸数据，求得$\Delta S=S_i-\overline{S},\Delta T=T_i-\overline{T}$。

3. 分别计算协方差矩阵$C_S,C_T$。

4. 求得形状和纹理协方差矩阵的特征值${\alpha }_i,{\beta }_i$和特征向量$s_i,t_i$。

5. 所以公式可以转化为：

   $$\{\begin{array}{l}{S}_{mod}=\overline{S}+\sum _{i=1}^{M-1}{\alpha }_i{s}_i\\ T_{mod}=\overline{T}+\sum _{i=1}^{M-1}{\beta }_i{t}_i\end{array}$$

注意：

• ${\alpha }_i,{\beta }_i$是根据大小值降序排列的
• 等式右边仍是$M$项，但是累加项降了一维，少了一项。
• 取$s_i,t_i$前几个分量可以对原始样本做很好的近似，因此可以大大减少需要估计的参数数目，并不失精度。

基于3DMM的方法，都是在求解这几个系数，后来的很多模型会在这个基础上添加表情、光照等参数，但是原理与之类似。

2.3 3DMM求解方法

前文提到，从二维图像重建真实的人脸三维形状和纹理，这个过程被称为Model Fitting，是一个病态问题（ill-posed problem）

经典的方法是1999年的文章“A Morphable Model for the Synthesis of 3D Faces”

A Morphable Model For The Synthesis Of 3D Faces-笔记 - 知乎 (zhihu.com)

其求解思路如下：

1. 初始化一个三维模型，需要初始化内部参数${\alpha }_i,{\beta }_i$，以及外部渲染参数，如相机位置、图像平面旋转角度、直射光和环境光的各个分量，图像对比度等20多维。有了这些参数之后就可以唯一确定一个3D到2D图像的投影。
2. 在初始参数的控制下，经过3D和2D的投影，即可由一个3D模型得到2维图像，然后计算与输入图像之间的误差。再以误差反向传播调整相关系数，调整3D模型，不断迭代。每次参与计算的是一个三角晶格，如果人脸被遮挡，则该部分不参与损失计算。
3. 具体迭代时采用由粗到精的方式，初始的时候使用低分辨率的图像，只优化第一个主成分系数，后面再逐步增加主成分。在后续一些迭代步骤中固定外部参数，对人脸各个部位分别优化${\alpha }_i,{\beta }_i$。

如果不需要十分精确，只需要获取人脸形状模型的应用来说，很多方法在使用3DMM时都会使用2D人脸关键点来估计出形状系数，具有更小的计算量，迭代也更加简单。

但是，存在如下缺点

• 病态问题本身并没有全局最优解，容易陷入不太好的局部优解
• 人脸的背景干扰以及遮挡会影响精度，而且误差函数本身不连续
• 对初始条件敏感，比如基于关键点进行优化时，如果关键点精度较差，重建的模型精度也会受到很大影响。

2.4 表情模型（Expression Model）

前面所提，“在2017和2019两个版本中，还提供了表情系数”，做出如下解释：

在2009年版本的数据集中，所有图像都是基于中性表情采集的，然而真实的人脸图像具有各种各样的表情。

2014年，FacewareHouse在3DMM的基础上增加了人脸表情，2017年作者们也对BFM模型进行了升级，增加了表情系数。

FaceWarehouse (kunzhou.net)

当前，基于3DMM的表情模型主要有两种，分别是加性模型和乘性模型。

• 加性模型即将表情作为形状的一个偏移量，如：
  $$c(W^s,W^e)=\overline{c}+E^s{W}^s+E^e{W}^e$$
  其中$\overline{c}$表示平均脸，$E^s$和$E^e$分别表示形状和表情基；$W^s$和$W^e$则是形状和表情基系数

• 与纹理模型不同，因为表情也会改变人脸的形状，因此它和形状并非完全正交的关系，所以有的研究者提出了乘性模型，如式：
  $$c(W^s,W^e)=\sum _{j=1}^{d_e}{w}_j^e{T}_j(c(W^s)+{\delta }^s)+{\delta }_j^e$$
  其中，$W^e$是一个表情迁移操作集合；第$j$个操作即为$T_j$；${\delta }^s$和${\delta }_j^e$是校准向量，$w_j^e$就是第$j$个$W^e$的系数

2.5 表现模型（Appearance Model）

模型受反射率和光照的影响，不过大部分3DMM不区分二者，所以我们将其视为一个因素，即反射率。

在2009年后提出的BFM模型中，该模型是一个线性模型，即由多个纹理表现基线性组合。后续的研究者们在此基础上增加了纹理细节，如脸部的皱纹等。

3. Shape from Shading（SfS）

从明暗恢复形状，即依据图像亮度（物体表面反射光的强度）与物体表面几何形状之间的关系，直接从灰度恢复出深度的一种技术。

原理：利用灰度图像的亮度信息，加上亮度生成原理，求得每个像素在3D空间中的法向量，最终根据法向量求得深度信息。

亮度信息由以下四个因素决定

• 光照，包括方向、位置和光的能量分布
• 物体表面的反射率，它决定了入射光在物体表面上如何被反射出去，一般由物体表面的材质决定
• 物体表面的几何形状
• 相机模型，包括内参和外参

3D模型通过光照及物体反射率，我们可以模拟相机，渲染出一张2D图片，SFS就是这个过程的逆过程。

4. Structure from Motion

是从一系列包含视觉运动信息的多张二维图像序列中估计三维结构的技术，基本步骤如下：

1. 图像特征点检测：每一对图像中的特征点进行匹配，只保留满足几何约束的点。
2. 迭代优化恢复摄像机的内参和外参

与立体视觉方法不同的是，立体视觉的多个摄像机之间的相对位置是通过标定给出来的，而SfM中的摄像机相对位置需要在重建之前进行计算。

三、深度学习三维人脸建模

1. 基于3DMM的方法

1.1 全监督3DMM

传统的方法需要去优化求解相关系数，而深度学习可以使用模型回归这些系数

以2017年提出的3DMM CNN方法为代表

Regressing Robust and Discriminative 3D Morphable Models with a Very Deep Neural Network | IEEE Conference Publication | IEEE Xplore

这是一篇讲单图实现3D重建方法的论文，整体流程概述：

1. 使用大量无约束照片来为每个主体（subject）拟合一个3DMM。
   • 它使用resnet101网络直接回归出3DMM的形状系数和纹理系数，各99维。
2. 首先将单个图像3DMM形状和纹理参数分别拟合到每个图像。然后，将同一受试者的所有3DMM估计值汇总在一起，为每个受试者提供一个估计值。
3. 这些汇集的估计用于代替昂贵的真实面部区域扫描来训练模型以直接回归3DMM的相关参数

存在以下问题

• 数据集的获取。真实的三维人脸和二位人脸图像对非常缺乏，采集成本高，作者用CASIA WebFace数据集中的多张图片进行Model Fitting求解生成了对应的三维人脸模型，将其作为真值（Ground Truth），进而得到二维三维图像对。

  Dataset之CASIA-WebFace：CASIA-WebFace 数据集的简介、安装、使用方法之详细攻略_一个处女座的程序猿的博客-CSDN博客

• 优化目标的设计。因为重建的结果是一个三维模型，所以损失函数是在三维的空间中计算，如果使用标准的欧几里得损失函数（Euclidean loss）来最小化距离，会使得到的人脸模型趋于平均化。对此，作者提出了非对称欧几里得损失（The asymmetric Euclidean loss），使模型学习到更多特征。
  $$L({\gamma }_p,\gamma )={\lambda }_1\cdot \underset{高估(over-estimate)}{\underbrace{||{\gamma }^{+}-{\gamma }_{max}|{|}_2^2}}+{\lambda }_2\cdot \underset{低估(under-estimate)}{\underbrace{||{\gamma }_p^{+}-{\gamma }_{max}|{|}_2^2}}$$
  其中，$$\begin{gathered} {\gamma }^{+}\doteq abs(\gamma )\doteq sign(\gamma )\cdot \gamma ;{\gamma }_p^{+}\doteq sign(\gamma )\cdot {\gamma }_p \\ {\gamma }_{max}\doteq max({\gamma }^{+},{\gamma }_p^{+}) \end{gathered}$$。

  $\gamma$是标签，${\gamma }_p$是预测值，通过两个权重${\lambda }_1$和${\lambda }_2$对损失的高估误差和低估误差进行权衡

  • ${\lambda }_1:{\lambda }_2=1:1$时，即为传统欧几里得损失函数
  • 作者设定${\lambda }_1:{\lambda }_2=1:3$，从而改变训练过程的行为，使其更快地摆脱欠拟合，鼓励网络生成更详细、更真实的 3D 面部模型。

除了上面这篇比较经典的之外，3DMM的相关研究者还提出了ExpNet（2018）用于预测表情系数，FacePoseNet（2017）用于预测姿态系数，验证了基于数据和CNN模型学习到相关系数的可行性。

• ExpNet: Landmark-Free, Deep, 3D Facial Expressions - Tal Hassner
• FacePoseNet: Making a Case for Landmark-Free Face Alignment | IEEE Conference Publication | IEEE Xplore

1.2 自监督3DMM

真实数据集存在获取困难、成本高、数据集少等问题，所以基于真实数据训练出来的模型鲁棒性有待提高。很多方法使用了仿真数据集，可以产生更多的数据进行学习，但是仿真数据集毕竟与真实的数据集分布有差异，以及由于头发等部位的缺失，导致模型泛化到真实数据集的能力较差。

基于此，基于自监督的方法被研究，这类方法不依赖真实的成对数据集，它将二维图像重建到三维，再反投影回二维图。这一类模型以MoFa方法为代表。

[1703.10580] MoFA: Model-based Deep Convolutional Face Autoencoder for Unsupervised Monocular Reconstruction (arxiv.org)

输入就是一张简单的2D图片，2D landmark是可选项，不一定要输入，输入的话可以加速模型的收敛
encoder的目的就是将图片编码为语义特征，即位姿，形状，表情，面部反射（纹理）和光照。
然后通过可微分的解码器将这些语义特征渲染（解码）成对应的3D模型，然后通过重构损失来无监督的训练整个模型。
中间可以引入2Dlandmark来加速模型的收敛。

1.3 与其他方法的结合

通常3DMM输入只有一张图像，假如输入更多有用的监督信息，有助于模型的优化，

如3DDFA（2018）框架：

二、Face Alignment in Full Pose Range: A 3D Total Solution（3DDFA）300w-lp数据集介绍:)年生的博客-CSDN博客

大多数人脸对齐算法都是针对中小型姿势（偏航角小于45°）的人脸设计的，缺乏对齐高达90°的大姿势（侧脸）中的人脸的能力。

挑战有三个方面。

• 常用的地标人脸模型假设所有地标都是可见的，因此不适合大姿势。
• 从正面视图到侧面视图，在大型姿势中，面部外观变化更大。
• 在大姿势中标记地标非常具有挑战性，因为必须猜测不可见的地标。

在该文中，作者建议在称为 3D 密集面部对齐（3DDFA）的新对齐框架中解决这三个挑战，其中通过级联卷积神经网络将密集 3D 可变形模型（3DMM）拟合到图像。同时，还利用 3D 信息来合成侧面视图中的人脸图像，为训练提供丰富的样本。

这是一个级联回归的过程。3DDFA框架将RGB图和PNCC（Projected Normalized Coordinate Code，投影归一化坐标代码）特征图进行通道拼装后作为输入，输出则是更新后的PNCC系数，包括6维姿态，199维形状和29维表情系数。

一个三维特征点表达为(x,y,z)和(r,g,b)值，将其归一化到0~1之后便称之为NCC（Normalized Coordinate Code，归一化坐标代码）。如果使用3DMM将图像往X-Y平面进行投影，并使用Z-buffer算法进行渲染，NCC作为Z-buffer算法的color-map，便可以得到PNCC。

除此之外，作者还引入了PAF（Pose Adaptive Feature，姿态自适应特征），网络图中的PAC是Pose Adaptive Convolution，就是一种对姿态适应的特征表示方法，通过将人脸的关键点投影到图像上，将图像中关键点之间的方向信息编码到PAF中。PAF的主要作用是在训练阶段将姿态信息引入模型中，以提高模型对姿态变化的鲁棒性和准确性。

由于不同维度的系数具有不同的重要性，作者对损失函数进行了精心的设计，通过引入权重，让网络优先你和重要的形状参数，包括尺度，旋转和平移。当人脸形状接近真值时，再拟合其他形状参数，实验证明这样的设计可以提升定位模型的精度。

由于参数化形状会限制人脸形变的能力，作者在使用3DFFA拟合之后，抽取HoG特征作为输入，使用线性回归来进一步提升2D特征点的定位精度。

3DDFA 的典型失败原因包括

• 复杂的阴影和遮挡
• 极端的姿势和表情
• 极端的照明和
• 鼻子上 3DMM 的有限形状变化

衍生版本：3DDFA-V2（2020），前一个版本注重静态建模研究，该版本注重模型动态变化研究，如相邻帧关联等问题。而且据论文表述，更准确、更稳定。工程没有公布训练代码，只公布了测试demo，可以将该工程当作跑数据的工具。相关资料：

• 一张图实现3D人脸建模，中科院博士生入选ECCV的新研究 (thepaper.cn)

• cleardusk/3DDFA_V2: The official PyTorch implementation of Towards Fast, Accurate and Stable 3D Dense Face Alignment, ECCV 2020. (github.com)

• 《Towards Fast, Accurate and Stable 3D Dense Face Alignment 》3DDFA-V2论文研读和工程实现_咆哮的大叔的博客-CSDN博客

1.4 3DMM的挑战

3DMM很经典，但已过去20年（自1999始）。虽然已从早期传统优化策略转向深度学习模型的系数回归，当前3DMM仍面临许多挑战：

• 受限于人脸，没有眼睛、嘴唇及头发信息。有时这些信息又很必要且有效。
• 较低维的空间参数，纹理模型较为简单，难以重建人脸皱纹等细节。
• 主要使用PCA提取主成分信息，但是可解释性太差，而且并不符合通常对人脸的描述，因此并不是一个很合理的特征空间。
• 有很多3DMM的变种，但是很少有这类模型能在各种场景下取得最优的效果。

2. 基于端到端的通用模型

随着深度学习的发展，研究人员开始研究使用CNN结构直接回归，端到端的重建三维人脸模型，而不是仅仅预测3DMM的系数，下面我们介绍其中代表。

2.1 PRNet

PRNet即Position map Regression Network，论文发表于2018年。

3D重建需要预测三维拓扑网格的顶点坐标，但是直接预测是有困难的，论文中提出了PRNet，它利用UV位置图（UV Position map）来描述3D形状。

PRNet论文简洁翻译_薛定谔的炼丹炉！的博客-CSDN博客

在BFM模型中，3D顶点数为53490个，PRNet的作者选择了一个大小为$256\times 256\times 3$的图像来对3D顶点进行编码，像素数目为$256\times 256=65536$，大于且接近53490。这个图被称为UV位置图，三个通道分别是X、Y、Z，分别记录了三维位置信息。值得注意的是，每个3D的顶点映射到这张UV位置映射图上都是没有重叠的。

有了上面的方法，就可以直接使用CNN预测UV位置图，采用一个编解码结构即可。

作者为了更好地预测，或者说使得预测出来的结果更有意义，计算损失函数时，对不同区域的顶点误差进行赋权，共四个区域：

• 特征点
• 鼻子、眼睛、嘴区域
• 人脸其他部分
• 脖子

他们的权重比例为16：4：3：0，可见特征点最重要，脖子不参与计算。

虽然这篇文章内容很多，但是很大的篇幅都在介绍过去方法的不足，实质性介绍本文方法的其实也不是特别多。其实现也不是特别复杂，但是这种维度转换的选择还是很巧妙的。

2.2 VRNet

人脸的三维重建可以等价为一个深度估计问题，当前基于CNN直接回归深度信息也有很多成功的案例。如果我们将三维空间离散化，然后预测每个三维空间的位置是否存在点，将所有的点组合起来也能够完成重建，这就是VRNet（2017）。

Large Pose 3D Face Reconstruction from a Single Image via Direct Volumetric CNN Regression阅读笔记 - 知乎 (zhihu.com)

Large Pose 3D Face Reconstruction from a Single Image via Direct Volumetric CNN Regression | IEEE Conference Publication | IEEE Xplore

VRNet（Volumetric Regression Network，体积回归网络）的核心思想，输入单张RGB图片，输出$192\times 192\times 200$大小的点云。它将3D顶点的预测问题，转换为3D的图像分割问题，使用了hourglass网络，预测是否属于人脸上的点（0或者1）。

其训练数据与3DDFA相同看，都是讲BFM和FaceWareHouse模型进行组合，即将FaceWareHouse模型中的表情基添加到BFM上（事实上前文提到的，BFM加上表情系数的时间，大约也就是此时），然后基于300W数据集进行Model Fitting得到模型的参数，将其重建结果作为真值，之后进行训练，损失采用sigmoid cross entropy loss。

另外，还可以将关键点检测作为额外的监督添加到模型中，得到VRNet-Guided模型，这可以进一步提升模型的精度。

其问题相当明显：

• 其丢弃了语义信息，CNN预测出来的3D人脸顶点是不固定的，需要进一步比对。
• 其重建分辨率较低，且大部分网络的输出点并不在曲面上，造成计算资源的浪费。

3. 人脸三维建模的其他难点

1. 传统的或改良的基于3DMM的方法最大问题就是结果过于平均，缺少细节。有的方法采用“粗+细”的方法，使用shape from shading的方法来捕捉细节，效果也不尽如人意。不管如何，要逼真的重建出人脸细节是很困难的。
2. 二维人脸信息一旦被遮挡，难以被精确地重建，除了利用人脸的对称先验信息进行补全外，有的方法借鉴了检索匹配的思路，即建立一个无遮挡的数据集，将重建的模型进行姿态匹配和人脸识别相似度匹配，然后经过2D对齐，使用基于梯度的方法来进行纹理迁移。但是显然这种方法对于未知的人脸是不敏感的。