Softmax分类器
损失函数
softmax的损失函数为
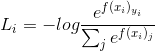
这里log的底数为e,即等价于
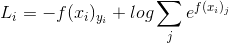
这里将最后得到的score归一化了。
SVM只选自己喜欢的男神,Softmax把所有备胎全部拉出来评分,最后还归一化一下。
损失函数求导
对于softmax损失函数的求导具体可以参考ufldl的Softmax回归,很详细。
自己理了下,首先 f(Xi)j = Wj * Xi,即 fj = Wj*Xi。
对W求偏导,对于正确类别的W分类器dWyi
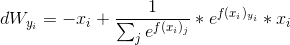
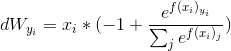
对于dWj
关于数值稳定
知乎翻译的notes里说,编程实现的时候数值可能非常大,做除法不稳定。 这里有一个trick,即分子分母同乘以一个数C,参考ufldl里Softmax回归模型参数化的特点 所验证的,一般把C取为 logC = maxXj*fj 。
代码形式如下
def softmax_loss_naive(W, X, y, reg):
"""
Softmax loss function, naive implementation (with loops)
Inputs have dimension D, there are C classes, and we operate on minibatches of N examples.
Inputs:
- W: A numpy array of shape (D, C) containing weights.
- X: A numpy array of shape (N, D) containing a minibatch of data.
- y: A numpy array of shape (N,) containing training labels; y[i] = c means
that X[i] has label c, where 0 <= c < C.
- reg: (float) regularization strength
Returns a tuple of:
- loss as single float
- gradient with respect to weights W; an array of same shape as W
"""
# Initialize the loss and gradient to zero.
loss = 0.0
dW = np.zeros_like(W)
#############################################################################
# TODO: Compute the softmax loss and its gradient using explicit loops. #
# Store the loss in loss and the gradient in dW. If you are not careful #
# here, it is easy to run into numeric instability. Don't forget the #
# regularization! #
#############################################################################
#pass
# Get shapes
num_classes = W.shape[1]
num_train = X.shape[0]
for i in xrange(num_train):
scores = X[i].dot(W)
shift_scores = scores - max(scores)
loss_i = - shift_scores[y[i]] + np.log(sum(np.exp(shift_scores)))
loss += loss_i
for j in xrange(num_classes):
softmax_output = np.exp(shift_scores[j]) / sum(np.exp(shift_scores))
if j == y[i]:
dW[:, j] += (-1 + softmax_output) * X[i]
else:
dW[:, j] += softmax_output * X[i]
loss /= num_train
loss += 0.5 * reg * np.sum(W * W)
dW = dW / num_train + reg * W
return loss, dWnum_classes = W.shape[1]
num_train = X.shape[0]
这两个数的取值注意下,,容易错
关于问题Why do we expect our loss to be close to -log(0.1)? Explain briefly.
这位大神做出了解释
Since the weight matrix W is uniform randomly selected, the predicted probability of each class is uniform distribution and identically equals 1/10, where 10 is the number of classes. So the cross entroy for each example is -log(0.1), which should equal to the loss.
因为迭代次数为1,W是随便取的,W接近于0,损失函数分子分母同时近似约去Wj(因为fj 远大于Wj),所以近似于1/10。最后loss接近于-log(0.1)(这是迭代一次的结果)。
之后的验证和svm差不多,最后得到的准确率为
softmax on raw pixels final test set accuracy: 0.334000
参考
http://ufldl.stanford.edu/wiki/index.php/Softmax%E5%9B%9E%E5%BD%92
https://zhuanlan.zhihu.com/p/21102293?refer=intelligentunit
http://www.cnblogs.com/wangxiu/p/5669348.html
https://github.com/lightaime/cs231n/tree/master/assignment1
http://cs231n.github.io/linear-classify/#softmax








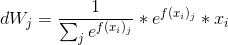














 1012
1012

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








