第六章 图 一、图的基本概念以及常见考点

目录

一、定义

二、分类

1.按箭头有无方向分为：

1、有向图

2、无向图

2.按简单复杂分为：

1、简单图

2、多重图

三、顶点的度

1、对于无向图:

2、对于有向图: 

四、顶点到顶点之间的关系描述

五、连通图，强连通图

1、连通图

常见考点:对于n个顶点的无向图G，若G是连通图，则最少有n-1条边若G是非连通图，则最多可能有条边

2、强连通图

常见考点:对于n个顶点的有向图G，若G是强连通图，则最少有n条边（形成回路)

六、子图

1、普通子图

2、生成子图

若子图包含所有原图的顶点，则称为生成子图。

七、连通分量！！！

八、生成树

九、边的权，带权图，带权网

十、几种特殊形态的图

1.无向完全图

​编辑

2、有向完全图

3、稀疏图和稠密图

4、无向图和有向树

---

一、定义

1、图G由顶点集V和边集E组成V。

2、用|V|表示图G中顶点的个数，也称为图的阶。

3、用|E|表示图G中边的条数。
 

注意:线性表可以是空表，树可以是空树，但图不可以是空，即V一定是非空集

当谈论图时，它通常指无向图，它的节点和边没有方向性，例如：

   

图的组成部分：

• 节点（顶点）：表示图中的对象或实体。
• 边：连接两个节点，表示它们之间的关系。边分为有向边和无向边。有向边有方向，而无向边没有方向。
• 权重：边上的权重可以表示两个节点之间距离、权值、花费等。
• 路径：路径是由一系列节点构成的序列，它们通过边相互连接。

图的存储方式：

• 邻接矩阵：使用二维数组来表示图。矩阵中的行和列分别代表节点，值表示它们之间的连通性。
• 邻接表：使用链表来存储节点和边，以此来表示图。
• 关联矩阵：使用二维数组来表示节点和边之间的关系。行表示节点，列表示边，值表示边是否与节点相连。

图论中的应用：

• 最短路径：找到一个节点到另一个节点的最短路径，例如 Dijkstra 算法和 Floyd 算法。
• 连通性：判断图中的节点是否连通，例如并查集和深度优先搜索。
• 最小生成树：找到一棵包含所有节点的最小权重连接树，例如 Prim 算法和 Kruskal 算法。
• 网络流：求解网络最大流问题，例如 Ford-Fulkerson 算法和 Edmonds-Karp 算法。
• 其他算法：拓扑排序、欧拉回路、哈密顿回路等。

二、分类

1.按箭头有无方向分为：

1、有向图

无向图使用圆括号表示两个相连的顶点。

2、无向图

有向图使用尖括号包含两个相连的顶点。

在括号里靠左边的且没有箭头的称为弧头；

在括号里靠右边的且拥有箭头的称为弧尾；

2.按简单复杂分为：

1、简单图

2、多重图

三、顶点的度

1、对于无向图:

顶点v的度是指依附于该顶点的边的条数，记为TD(v)。

例：

连向A的线有1条；连向B的线有3条；连向C的线有2条；连向D的线有3条；连向E的线有3条；

重复的线也要算上

所以TD(v)=1+3+2+3+3=12;

即无向图的全部顶点的度的和等于边数的2倍,TD(v)=2|E|

2、对于有向图: 

入度是以顶点v为终点的有向边的数目，记为ID(v);

出度是以顶点v为起点的有向边的数目，记为OD(v)。

顶点v的度等于其入度和出度之和，即TD(v)= ID(v)+ OD(v)。

例：

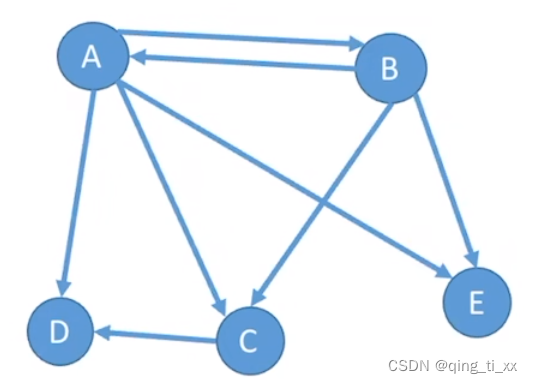
顶点A的入度为1，出度为4，总度数之和为5.

在具有n个顶点、e条边的有向图中，所有顶点的入度之和=所有顶点的出度之和=e

四、顶点到顶点之间的关系描述

路径――顶点vp,到顶点vq之间的一条路径是指顶点序列，Vp,Vi,Vi

回路――第一个顶点和最后一个顶点相同的路径称为回路或环

简单路径――在路径序列中，顶点不重复出现的路径称为简单路径。

简单回路――除第一个顶点和最后一个顶点外，其余顶点不重复出现的回路称为简单回路。

路径长度――路径上边的数目

点到点的距离――从顶点u出发到顶点v的最短路径若存在，则此路径的长度称为从u到v的距离。若从u到v根本不存在路径，则记该距离为无穷( oo )

无向图中，若从顶点v到顶点w有路径存在，则称v和w是连通的

有向图中，若从顶点v到顶点w和从顶点w到顶点v之间都有路径，则称这两个顶点是强连通的

五、连通图，强连通图

1、连通图

若图G中任意两个顶点都是连通的，则称图G为连通图，否则称为非连通图。（无向图）

常见考点:
对于n个顶点的无向图G，
若G是连通图，则最少有n-1条边
若G是非连通图，则最多可能有条边
 

2、强连通图
 

若图中任何一对顶点都是强连通的，则称此图为强连通图。（有向图）

常见考点:
对于n个顶点的有向图G，
若G是强连通图，则最少有n条边（形成回路)

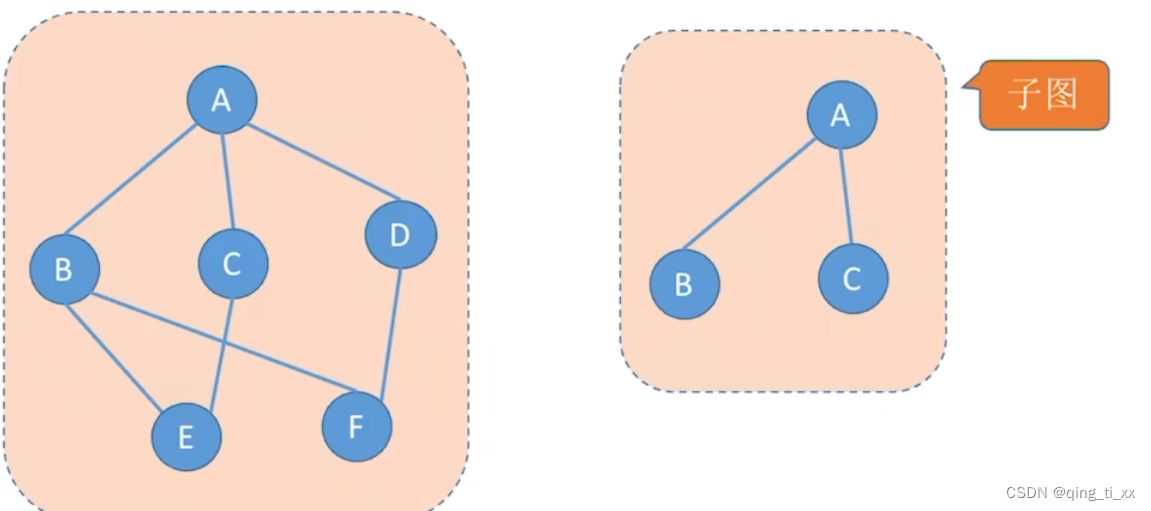
六、子图

1、普通子图

点是原无向图子集，边是原无向图的子集。（有向图相同）

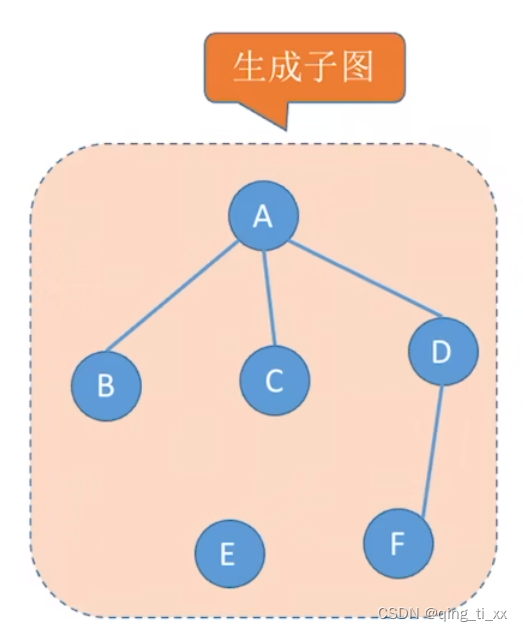
2、生成子图

若子图包含所有原图的顶点，则称为生成子图。

七、连通分量！！！

要尽可能包含多的连通顶点↓

要尽可能包含多的强连通顶点↓

八、生成树

包含所有顶点，且用最少的边使它形成连通子图

若图中顶点数为n，则它的生成树含有n-1条边。对生成树而言，若砍去它的一条边，则会变成非连通图，若加上一条边则会形成一个回路。
 

九、边的权，带权图，带权网

1、边的权—―在一个图中，每条边都可以标上具有某种含义的数值,该数值称为该边的权值。

2、带权图/网――边上带有权值的图称为带权图，也称网。

3、带权路径长度――当图是带权图时，一条路径上所有边的权值之和，称为该路径的带权路径长度

十、几种特殊形态的图

1.无向完全图

2、有向完全图

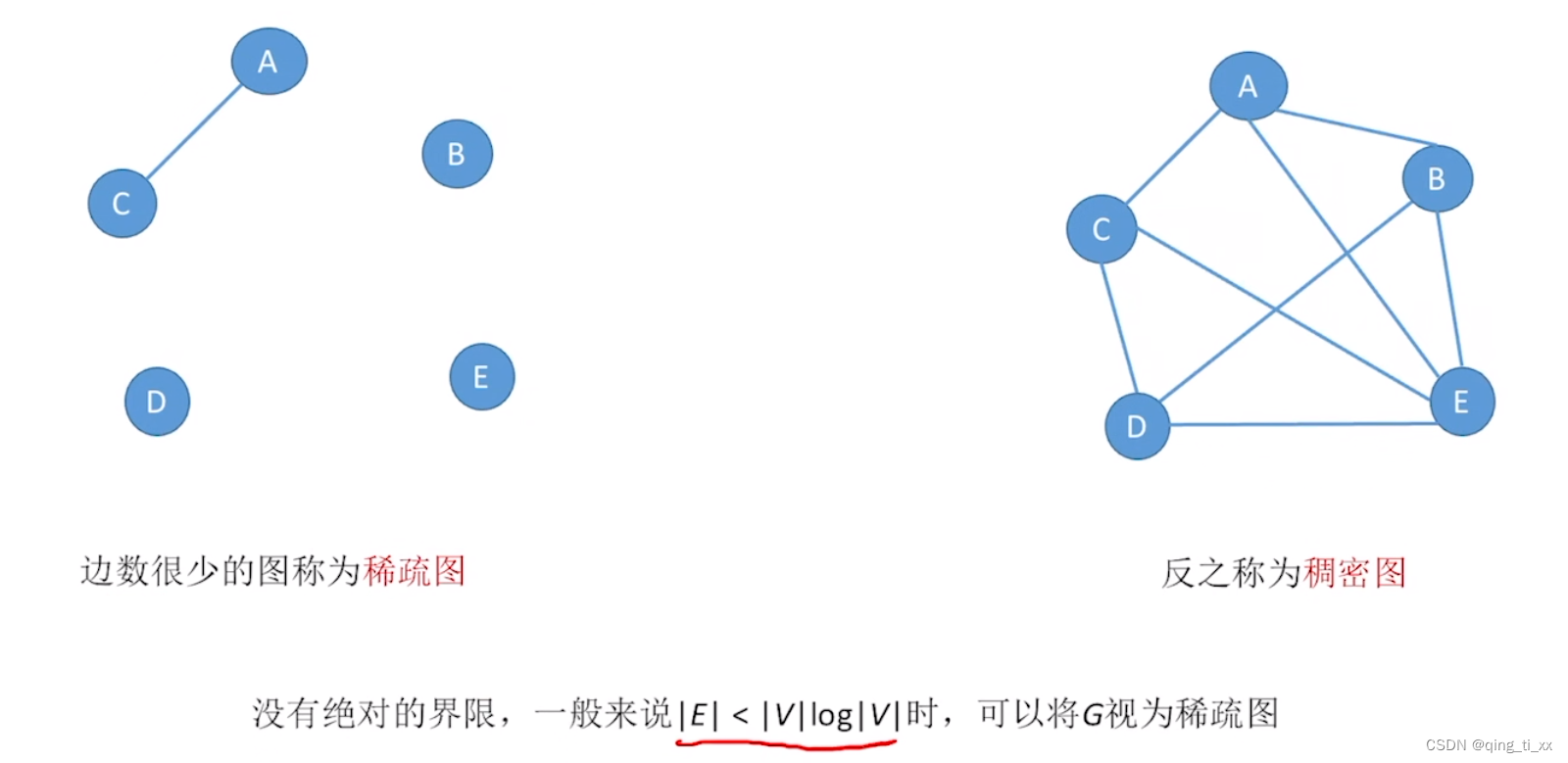
3、稀疏图和稠密图

4、无向图和有向树