信息度量
信息论中,把信息大小解释为其不确定度。如果一个事件必然发生,那么他没有不确定度,也就不包含信息。即信息=不确定度。
借用数学之美中的一个例子:
马上要举行世界杯赛了。大家都很关心谁会是冠军。假如我错过了看世界杯,赛后我问一个知道比赛结果的观众“哪支球队是冠军”? 他不愿意直接告诉我, 而要让我猜,并且我每猜一次,他要收一元钱才肯告诉我是否猜对了,那么我需要付给他多少钱才能知道谁是冠军呢? 我可以把球队编上号,从 1 到 32, 然后提问: “冠军的球队在 1-16 号中吗?” 假如他告诉我猜对了, 我会接着问: “冠军在 1-8 号中吗?” 假如他告诉我猜错了, 我自然知道冠军队在 9-16 中。这样只需要五次, 我就能知道哪支球队是冠军。所以,谁是世界杯冠军这条消息的信息量只值五块钱。
如果我们再考虑不同球队获胜的不同比例,如巴西比例高,中国比例低些,那么结果又会不同。
互信息,联合熵,条件熵的相关定义
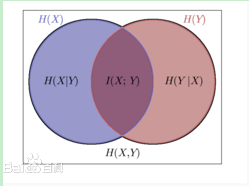
这样一幅图:
两个随机变量,X,Y。
H(X)表示其信息量,也就是自信息
H(X|Y)表示已知Y的情况下X的信息量,同理,H(Y|X)也是。
H(X,Y)表示X,Y的联合熵,也就是这两个变量联合表示的信息量。
H(X;Y),也就是I(X;Y),也就是互信息,指的是两个变量重复的部分。
H(X;Y)=H(X,Y)- H(X|Y)- H(Y|X),这个等式从上图也能形象地看出。
KL距离
KL距离用来度量两个分布的相似度。
物理意义:在相同事件空间里,概率分布P(x)的事件空间,若用概率分布 Q(x)编码时,平均每个基本事件(符号)编码长度增加了多少比特。
另一种理解就是,已知Q的分布,用Q分布近似估计P,P的不确定度减少了多少。
我们用D(P||Q)表示KL距离,计算公式如下:
也就是用一个分布来表征另一个分布的额外不确定度。
P(X)=Q(X),他们的KL距离为0;否则,差异越大,距离越大。
上述KL距离物理意义的表述,在许多运用中都有很好地体现。
事例:
南京的天气为随机变量D,某个南京的同学的穿着W。我想通过W,了解D。也就是用P(D/W)来近似P(D),现在定量地计算我们通过穿着,了解了多少关于天气的信息。
也就是用P(D/W)来代替P(D)编码,减少了多少不确定度?
用KL距离来表征,就是:D(P(D/W)||P(D))。
接着,如果已知一个穿着wi,可以选择最大KL距离D(P(dj/wi)||P(dj))的dj,也就是最可能的天气。
这就是KL距离的物理意义在实际中的一些运用。
互信息与KL距离
插入一个概念:独立与相关。
概率中的相关概念指的是线性相关,而是否独立,则取决于线性以及非线性的关系。
区别:
X,Y的互信息I(X,Y)表征其独立程度,KL距离表征其线性相关性。如下图:
联系:
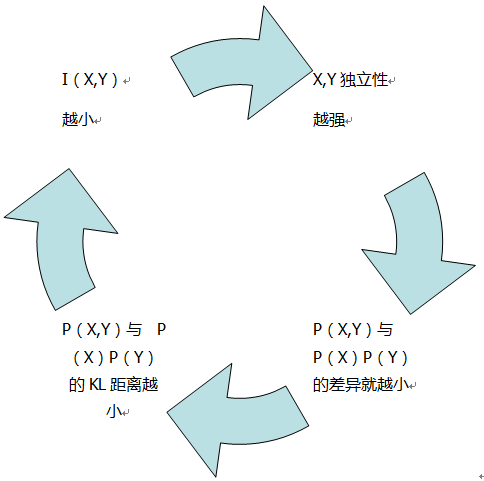
X,Y的互信息也就是P(X,Y)与P(X)P(Y)的KL距离。
下面这幅图描绘他们之间的联系:
还有下面这个公式:
这个等式描绘了上面举的天气和穿着的例子,用P(Y|X)来代替P(Y),不确定度减少了多少?其关于X求和后就是X,Y的互信息。
上式也是许多运用中常见的等式:
我们可以通过互信息与KL距离的这种关系,构造一定的互信息,从而处理一些实际问题。
皮尔森相关系数与KL距离:
联系:皮尔森相关系数衡量X,Y的线性相关性。这与KL距离类似。
区别:
比较明显的区别就是,KL距离是不对等的度量距离,而皮尔森相关系数是对等的度量距离。
实际运用:
如上面天气与穿着的例子,以及KL距离与互信息的相互关系。一般运用这些知识,在信息检索,自然语言处理方面都有相关运用。








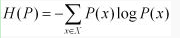

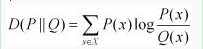



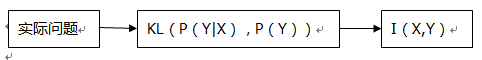

















 4068
4068

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








