一个简单的最优化问题如下:
在二维空间上寻找函数的最大值。
一般我们常见的解析法,是求导,得极值点。这里不再讨论。
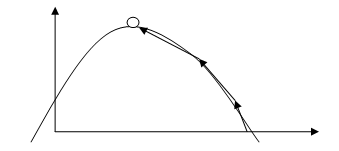
很多情况下解析法很难求解,常会用到一种迭代慢慢逼近的方法,就是迭代法。如下图。
迭代法由一个基本的可行点出发,依次产生一个可行点列,x1,x2,…,xk,f(xk+1)<f(xk),并且使得某个xk恰好是问题的一个最优解。
迭代法基本步骤如下:
1. 一个初始的位置x0;
2. 一个迭代搜索的方向p
3. 一个前进的步长a.
最速下降法
一个很自然的问题,关于目标函数f(x),我们要选择哪个方向才能够下降最快呢?
由Taylor公式有:
其中a表示步长,p表示方向。
当a一定时,p取-g(x)方向,能够使得f(x+ap)最小,也就是当前下降最快,即
为最速下降方向。
如果做精确的搜索,那么我们可以求得一个精确的步长:
不过精确搜索计算量过大,一般不采用这种方法,而是任意指定一个可行的步长。
关于收敛性:
经证明,最速下降法是整体收敛的,且为线性收敛,收敛速度较慢。
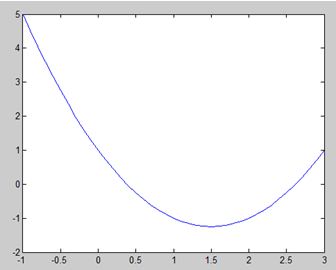
用matlab求解Y=X^2-3X+1,如下:
clear;
clc;
X=-1:0.1:3;
Y=X.*X-3*X+1;
e=0.0001;
a=0.5;
e_temp=1;
x=-1;
count=0;
while(e_temp>e)
p=2*x-3;
x_temp=x;
x=x-a*p;
e_temp=x-x_temp;
count=count+1;
end
minY=x*x-3*x+1
minX=x
count
plot(X,Y);
图:
结果为:
minY =
-1.2500
minX =
1.5000
迭代次数:2
Newton法
最速下降法以线性的Taylor展开得出下降方向,本质使用线性函数假设目标函数。我们想要达到更快的收敛,需要考虑对目标函数的高维逼近。
我们把f(x)看做关于xk的一个二维函数,然后用解析法求出二维函数的精确最小值,得到xk+1。
首先,f(x)在xk处Taylor展开,只保留到二次:
我们把xk当做已知变量,x为未知,用解析法直接求解x,得到近似值。
如果f(x)是二次函数,那么Newton法一次就能得到最优值。
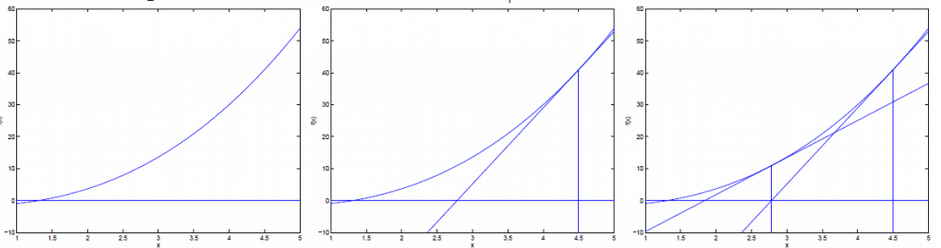
另一种更直观的解释:
假设函数f(x),如下,现在要求解f(x)的零点。
可以按照上图中的方法迭代求解,每次的更新如下:
现在,对于l(x),我们要求其最小值,也就是l'(x)=0的点。参照上面的方法,我们有如下更新:
收敛性:
只有当初始点x0充分接近极小点时,才能保证收敛,否则直接扔掉二次以后的Taylor项,会导致局部收敛,而且每次迭代都要计算G,如果G是奇异的,还不能得到解。
Newton是二次收敛的,是其最大优势。
Matlab求解Y=X^3+10X^2+1,如下:
clear;
clc;
X=-1:0.1:3;
Y=X.*X.*X+10*X.*X+1;
e=0.0001;
e_temp=1;
x=-1;
while(e_temp>e)
G=6*x+20;
p=(3*x*x+20*x)/(G);
x_temp=x;
x=x-p;
e_temp=x-x_temp;
end
minY=x*x-3*x+1
minX=x
plot(X,Y);
图:
结果:
minY =
0.9806
minX =
0.0065
迭代次数:2
同样是通过Taylor展开得到的方向,最速下降法取其一次部分,假设函数为线性。而Newton法取二次,假设函数维二次,会有更快的收敛速度,不过也有上述的种种问题。
对于Newton的缺点,改进的有相应的阻尼Newton等等方法。









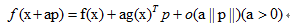
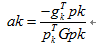
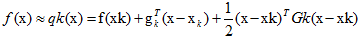

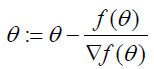
















 2810
2810

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








