无向图的双连通性

目录

无向图的双连通性

• 相关概念
• 关节点：若在删去顶点a以及与之相邻的边之后，图G被分割成两个或
  两个以上的连通分量，则顶点a为连通无向图的关节点
  
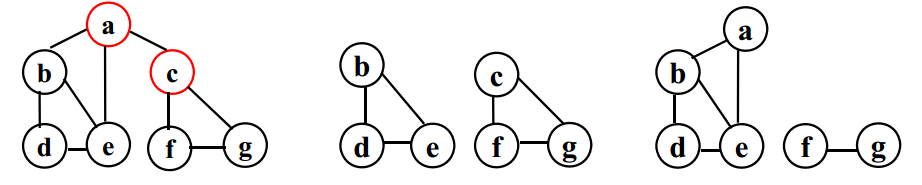
• 双连通图：没有关节点的连通图称为双连通图（ Biconnected Graph） 。
• 等价边集：称连通图G=(V, E)的边e1 和 e2 是等价的，若 e1=e2 或者有一条环路包含 e1又包含 e2 。
• 双连通分量：设 Vi是等价边集 Ei 中各边所连接的顶点集（ 1≤i≤k） , 每个图Gi = ( Vi, Ei ) 叫做 G 的一个双连通分量。
• 在双连通图上, 任何一对顶点之间至少存在有两条路径，在删
  去某个顶点及与该顶点相关联的边时, 也不破坏图的连通性。
• 双连通的无向图是连通的，但连通的无向图未必双连通。
  -如果连通图不是双连通图，则它可以包括几个双连通分量。
• 关节点性质
• 由关节点可以判断图是否双联通
• 由深度优先生成树可得出两类关节点的特性：
• 第一类关节点：若生成树的根有两株或两株以上子树， 则此根结点必为关节（ 第一类关节点） 。 因为图中不存在连接不同子树中顶点的边， 因此， 若删去根顶点， 生成树变成生成森林。
• 第二类关节点：若生成树中非叶顶点v，其某株子树的根和子树中的其它结点均没有指向v 的祖先的回退边，则v 是关节点（ 第二类关节点）。因为删去v，则其子树和图的其它部分被分割开来。
• 

---

R.Tarjan算法–求关节点的算法

1. 计算先深编号： 对图进行先深搜索， 计算每个结点v的先深编号dfn[v]，形成先深生成树S=(V,T)。
2. 计算low[v]：在先深生成树上按后根遍历顺序进行计算每个顶点v的 low[v] ， low[v]取下述三个结点中的最小者：
   dfn[v]；
   dfn[w]， 凡是有回退边(v,w)的任何结点w；
   low[y]，对v的任何儿子y。
   若某个顶点V，存在孩子结点y，且low[y]>=dfn[v],则v必为关节点。因为此时表明，y及其子孙均无指向V的祖先的回退边
   3.求关节点：
   3.1 树根是关节点，当且仅当它有两个或两个以上的儿子(第一类关节点)；
   3.2 非树根结点v是关节点当且仅当v有某个儿子y，使low[y]≥dfn[v] (第二类关节点)
   时间复杂度：O（n+e）
3. 示例：
   注：连通图：G=(V,E)，先深生成树：S=(V,T),回退边之集：B
   按后根遍历顺序计算low[v]编号和求关节点
   
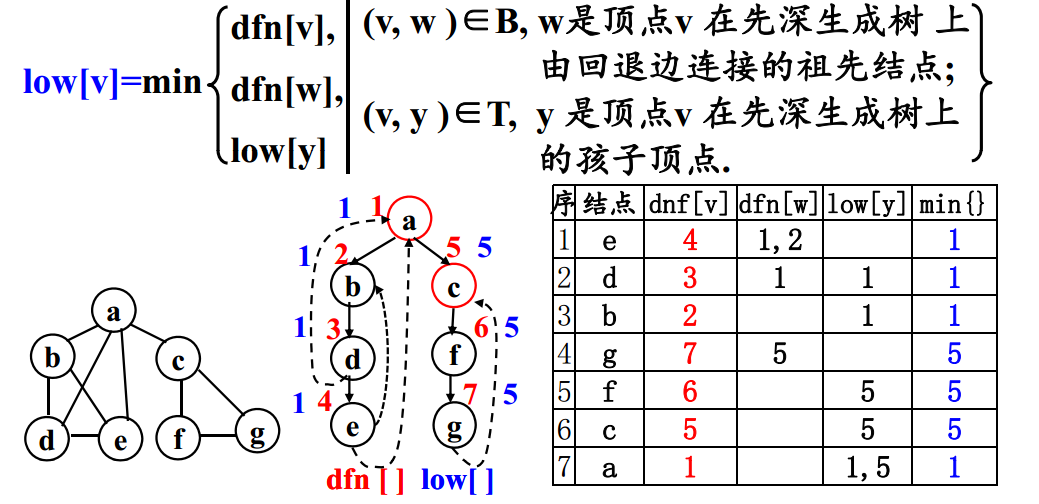
   结论：
   1.根结点a有两个孩子，是关节点；
   2.(c, f)是树边即f是c的孩子且low[f] ≥ dnf[c]，所以c是关节点。
4. 求关节点的R.Tarjan算法实现—同先深搜索算法

代码实现

void FindArticul(AdjGraph G)
{ 
/*连通图G 以邻接表作存储结构，查找并输出G 上全部关节点*/
count=1; /*全局变量count 用于对访问计数*/
dfn[0] =1; /*设定邻接表上0 号顶点为生成树的根*/
for(i=1;i<G.n;++i) dfn[i]=0; /*其余顶点尚未访问， dfn[]兼职visited[]*/
p=G.vexlist[0].firstedge; v=p->adjvex;
DFSArticul(v); /*从顶点v 出发深度优先查找关节点**/
if(count<G.n) { 
/*生成树的根至少有两棵子树*/
cout<<G.vexlist[0].vertex); /*根是关节点，输出*/
while(p->next) {
p=p->next;
v p =p->adjve ; x;
if(dfn[v]==0) DFSArticul(v);
}//while
}//if
} //FindArticul

void DFSArticul(int v0)
/*从顶点v0 出发深度优先遍历图G，计算low[]，查找并输出关节点 */
{ dnf[v0]=min=count++; /*v0 是第count 个访问的顶点*/
for(p=G.vexlist[v0].firstedge; p; p=p->next) /*对v0 的每个邻接点检查*/
{ w=p->adjvex; /*w 为v0 的邻接点*/
if(dnf[w]==0) /*若w 未曾访问，则w 为v0 的孩子*/
{ DFSArticul(w); /*返回前求得low[w]*/
if(low[w]<min) min=low[w];
if(low[w]>=dfn[v0])
cout<<G vexlist[v0] vertex); / .vexlist[v0].vertex); /*输出关节点*/
}
else if(dfn[w]<min) min=dfn[w];
/*w 已访问， w 是v0 在生成树上的祖先*/
}//for
low[v0]=min;
}//DFSArticul