- 单变量线性回归 (matlab)
- 多变量线性回归 (matlab)
- 基于Logistic回归和Sigmoid函数的分类 (matlab、python)
- 梯度上升法
- 改进的梯度上升法
- matlab、python实现一个实例
==================================================
1 单变量线性回归
回归与分类的区别: 定量输出为回归,定性输出为分类。
一般的机器学习任务:
输入数据 —–> 模型(hypothesis : h(x)) —–> 输出数据。
在监督学习中,前后都知道,只有模型是我们需要学习的。
我们期望找到一个
h(x)
,对于单变量 一般地:
h(x)=θ0+θ1x
(
θ
未知)
对于多变量:
h(x)=θ0+θ1x1+....+θnxn
(将会在第二节介绍)
目标:
找到合适的
θ0
和
θ1
,对于给定的样本使 h(x) 尽可能的接近于真是值 y
相应的提出:代价函数: 所有训练样本的误差累积和:
J(θ0,θ1)=12m∑mi=1(hθ(x)−yi)2
注: 前面分目的2是为了 后面求偏导时候的方便。
至此,我们的目标就变为希望 J(θ0,θ1) 越小越好。
求解J的最小值—梯度下降法
基本思路:从确定的参数
θ
开始。不断更改该参数,直到达到最佳的值,或者可接受的范围内。
==================
梯度下降法:
repeat until vonvergence{
θj:=θj+αΔJ(θ0,θ1)
}
Δ
表示梯度
α
表示步长,如果步长太大,优化过程中会发生震荡。如果太小,优化过程国语缓慢。一般地。一般选择0.001 - 0.003
==================
注: 梯度下降一定会达到一个最优值,(不能确定是局部最优,还是全局最优)
两种常见的梯度下降方法:
批量梯度下降法 和 随机梯度下降法
区别: 前者是计算所有样本的误差之和来更新参数,后者每次只需要一个样本来更新参数。
当样本数量过大的时候,前者显然过于缓慢。
对于上面的线性回归模型: 批量下降算法
h(x)=θ0+θ1x
J(θ0,θ1)=12m∑mi=1(hθ(x)−yi)2
ΔJθ0=1m∑mi=1(hθ(x)−yi)
ΔJθ0=1m∑mi=1(hθ(x)−yi)xi
随机梯度下降
注:同步更新两个参数。
简化算法: 矩阵表示形式
在上面的批量梯度下降算法中,每次更新一个参数都要循环m次。
通过矩阵形式可以简化:
h(x)=θ0+θ1x1=θ0x0+θ1x1
其中
x0=1
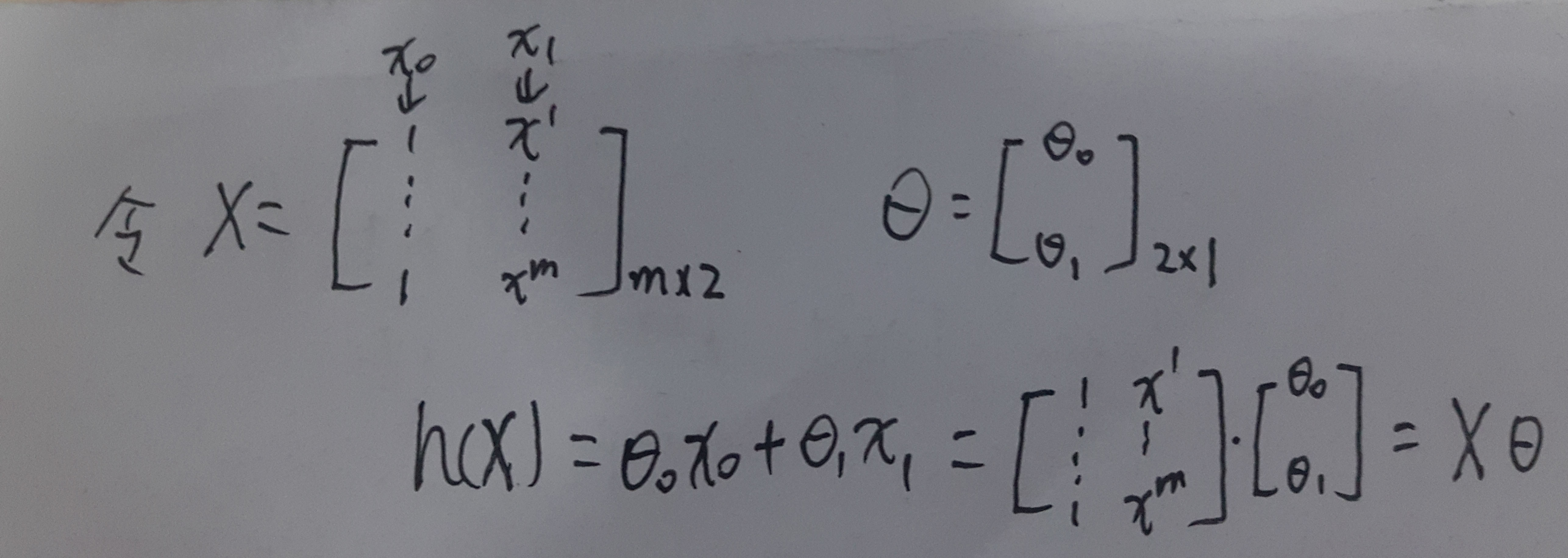

代码实现:
matlab:
function [theta,J] = B_gradientDescent(X,y,alpha,num_iters)
% 批量梯度下降法
%输入 X:训练数据矩阵 m*n (m个n维训练样本) y: 真实值 m*1 alpha: 步长
% num_iters: 迭代次数
% 输出: theta 参数值 J 代价函数
[m,n] = size(X);
J = zeros(num_iters,1) % 存储代价函数
theta = ones(n,1) %初始值
for iter = 1:num_iters
h = X*theta;
delta1 = y - h; % 误差 m*1
delta = repmat(delta1,1,n).*X; % 注意是点乘
theta = theta - alpha/m*sum(delta)' %sum 默认列相加 转置是为了维数一致
J(V) = (h-y).^2;
J = 0.5/m*sum(J(v));
end function theta = R_gradientDescent(X,y,alpha)
% 随机梯度下降
[m,n] = size(X);
theta = ones(n,1) %初始值
for i=1:m
h = X(i,:)*theta;
error = y(i)-h;
theta = theta - alpha* error * X(i,:)';
end多变量线性回归
对于多变量与单变量的原理一样。 在实现中,我们要考虑一个实际问题: 特征归一化
1 均值归一化 (x-min)/(max-min)
funciton x_norm = meanNormalize(X)
[m,n]=size(x);
x_norm = zeros(m,n);
temp0 = repmat(min(x),m,1);
temp1 = repmat((max(x)-min(x)),m,1)
x_norm = (x-temp0)./temp1; 2 Z-score标准化方法 (x-mu)/(标准差)
funciton x_norm = featureNormalize(X)
[m,n]=size(x);
x_norm = zeros(m,n);
mu = zeros(1,n);
sigma = zeros(1,n);
mu = mean(x);
sigma = std(x);
temp0 = repmat(mu,m,1);
temp1 = repmat(sigma,m,1)
x_norm = (x-mu)./temp1; 多变量线性回归 可以用上面的梯队下降法进行求解,也可以采用Normal equation来求解:

该方法中:特征不需要归一化。
实例 房价预测
原始数据: 前两列 为特征,最后一列为房价。
clc,clear;
data = load('data.txt');
x = data(:,1:2);
y = data(:,3);
[m,n] = size(x);
x = featureNormalize(x); %归一化
x = [ones(m,1) x]; % 第一列加上1
% 梯度下降
alpha = 0.001;
num_iters = 500;
[theta,J] = B_gradientDescent(X,y,alpha,num_iters);
% 画出代价函数
figure;
plot(J_history, '-b', 'LineWidth', 2);
xlabel('Number of iterations');
ylabel('Cost J');
% 预测
price = 0;
x_new=[1650 3];
x_new = featureNormalize(x_new); %归一化
x_new = [ones(m,1) x_new]; % 第一列加上1
price = x_new * theta;
fprintf(['预测房价:\n $%f\n'], price);基于Logistic回归和Sigmoid函数的分类
利用Logistic回归进行分类的主要思想是: 根据现有数据对分类边界线建立回归公式,以此进行分类。
我们期望的函数是: 能接受所有输入然后预测出类别。最常用的就是sigmoid函数(在两个类的情况下,函数输出0或1)
f(x)=11+e−x
本函数特殊之处:
f′(x)=f(x)(1−f(x))
证明过程简单,这里不介绍。
实现Logistic回归分类器: 可以在每一个特征上都乘上一个回归系数,然后将所有结果相加,最后将总和输入Sigmoid函数,得到0-1之间的数值,大于0.5的分类为1,小于的分类为0。
那么我们的求解过程就变为最佳回归系数的求解(相当于权重)
对于Sigmoid函数的输入Z:
Z=w0x0+w1x1+....+wnxn
注: 上述公式可以用 Z=WTX 向量形式表示 这里的 x0 仍为1。
梯度上升法: 找到某函数最大值。
梯度下降法: 找到某函数最小值。
两者唯一区别: 在参数优化过程中, 一个是 +,一个是 -
训练算法: 使用梯度上升法找到最佳参数。
原始数据:
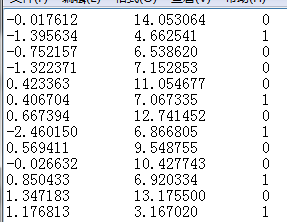
前两列为 样例 最后一列为标签。
##Python代码
from numpy import *
def loadData():
dataMat = []
labelMat = []
fr = open('testSet.txt')
for i in fr.readlines(): # 按行读取 返回列表 list
line = i.strip().split() # s.strip(rm) s为字符串,rm为要删除的字符序列。 split() 分割后 返回列表 (注a)
dataMat.append([1.0, float(line[0]), float(line[1])]) # 输入数据矩阵
labelMat.append(int(line[2]))
return dataMat, labelMat
def sigmoid(z):
return 1.0/(1+exp(-z))
def grandAscent(data, label): # 输入样例和真实标签
dataMat = mat(data) # 变换为矩阵数据形式 array是变为数组
labelMat = mat(label)
m,n = shape(dataMat) # 相当于 Matlab 的size()
alpha = 0.001
iter_num =500
weights = ones((n,1)) # 生成全为 1 的矩阵
for i in iter_num:
h =sigmoid(dataMat * weigths) # 相当f(x)
error = labelMat.transpose() - h
weights = weights + alpha * dataMat.transpose() * error
return weights (a)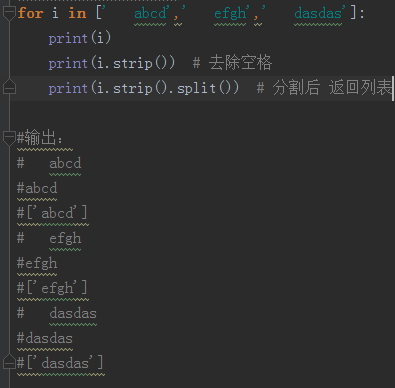
(b)分析上面的Matlab与Python代码。虽然写法不同但效果相同:








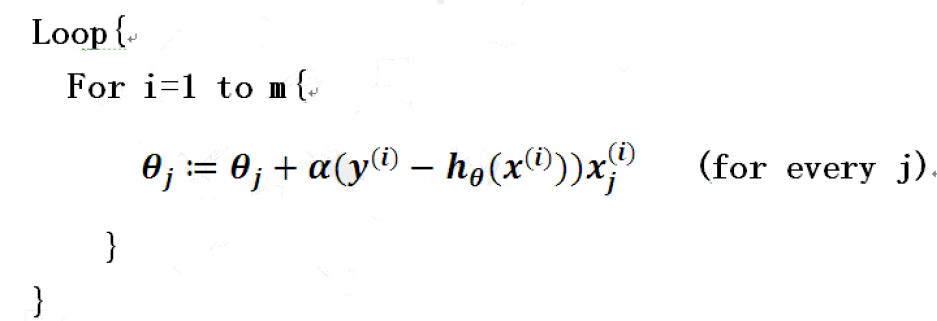


















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








