频域处理相关

Gabor 变换 Gabor函数

在图像处理、模式识别以及计算机视觉等领域中，Gabor 滤波器得到了广泛的应用。 用Gabor 函数形成的二维Gabor 滤波器具有在空间域和频率域同时取得最优局部化的特性，与人类生物视觉特性很相似，因此能够很好地描述对应于空间频率(尺度)、空间位置及方向选择性的局部结构信息。

　　Gabor变换是一种短时傅里叶变换方法，其实质是在傅里叶变换中加入一个窗函数，通过窗函数来实现信号的时频分析。当选取高斯函数作为窗函数时，短时傅里叶变换称为Gabor变换。

常用的偶对称二维Gabor滤波器可表示为：

1. 不同方向下的Gabor滤波器：

　　　　　　　　　　　　　　　　　　　　图1 不同方向上的滤波器

　　在实际应用时，可以根据检测对象的方向趋势，选择合适的方向参数进行滤波。如在检测人脸的五官时，可以根据人脸的偏转角度进行滤波，可以使特征点的定位更加准确。

　　2.  不同频率下的滤波器：

　　　　　　　　　　　　　　　　　　　　　　图2 不同频率下的滤波器

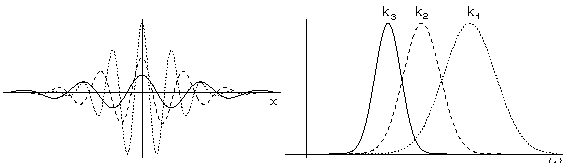
　　从图2可以看出随着的变化，Gabor滤波器中出现了很多宽窄与纹理不同的明暗条纹。当滤波器纹理与图像作用时，滤波器覆盖下的局部纹理频率与滤波器的频率越接近响应就越大，反之越小。

Gabor变换属于加窗傅立叶变换，Gabor函数可以在频域不同尺度、不同方向上提取相关的特征。另外Gabor函数与人眼的生物作用相仿，所以经常用作纹理识别上，并取得了较好的效果。

Gabor变换是短时Fourier变换中当窗函数取为高斯函数时的一种特殊情况.

Gabor变换的本质实际上还是对二维图像求卷积。因此二维卷积运算的效率就直接决定了Gabor变换的效率。在这里我先说说二维卷积运算以及如何通过二维傅立叶变换提高卷积运算效率.关于离散二维叠加和卷积的运算介绍的书籍比较多，我这里推荐William K. Pratt著，邓鲁华 张延恒等译的《数字图像处理（第3版）》，其中第7章介绍的就是这方面的运算.

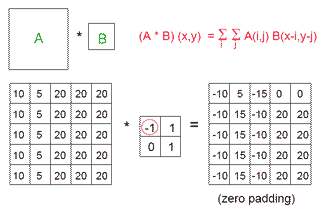
A可以理解成是待处理的笔迹纹理，B可以理解成Gabor变换的核函数，现在要求A与B的离散二维叠加卷积，我们首先对A的右边界和下边界填充0（zero padding)，然后将B进行水平翻转和垂直翻转，如下图：

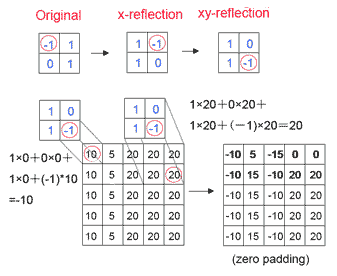
然后用B中的每个值依次乘以A中相对位置处的值并进行累加，结果填入相应位置处（注意红圈位置）。通常二维卷积的结果比A、B的尺寸要大。如下图所示：

2、快速傅立叶变换卷积

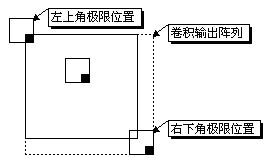
根据傅立叶变换理论，对图像进行二维卷积等价于对图像的二维傅立叶变换以及核函数的二维傅立叶变换在频域求乘法。通过二维傅立叶变换可以有效提高卷积的运算效率。但在进行傅立叶变换时一定要注意“卷绕误差效应”，只有正确对原有图像以及卷积核填补零后，才能得到正确的卷积结果。

二维Gabor函数可以表示为：

 

 

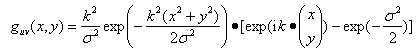
其中:

 

 

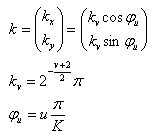
v的取值决定了Gabor滤波的波长，u的取值表示Gabor核函数的方向，K表示总的方向数。参数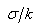决定了高斯窗口的大小，这里取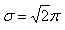. 程序中取4个频率（v=0, 1, ..., 3），8个方向（即K=8，u＝0, 1, ... ,7），共32个Gabor核函数。不同频率不同方向的Gabor函数可通过下图表示：

 

 

 

 

 

 

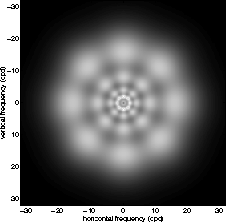
所谓目标识别，从某种意义上说就是特征识别的问题。而红外图特征提取的角度一般可以从几何形状和上下文的判断中得到，比如说，当你在一幅图像中去搜索桥梁和机场的跑道的时候，我们可以从形状上发现他们都是一组平行线；然后基于上下文去判断，桥梁的长度肯定比跑道短，桥梁的两边一般是水域，而跑道的中间有一些联络道，而这些这些联络道本身也是平行线。

通常用这种仅仅利用图像本身的知识去判断的时候，时常由于经验的限制，识别率总是没有办法做到很好！虽然图像所一些早期的论文里都声称，识别率能够达到90％以上，但是那只是用自己搜集的有利于自己算法的图片得出来的结果而已！

言规正传，由于种种努力，我们发现了频率的概念࿰