【算法设计zxd】第一章算法基础 4.设计工具【三角矩阵，】

羰基绳命

已于 2022-04-21 20:48:34 修改

阅读量1.6k

点赞数

分类专栏：算法算法zxd 文章标签：算法 p2p fpga开发

于 2022-01-22 00:57:56 首次发布

本文链接：https://blog.csdn.net/iivan_cpp/article/details/122631630

版权

1. 循环设计

(1) 设计思维

自底向上的设计（Down - Top Design）

自顶向下的设计（Top-Down Design）

(2)挖掘内在规律构建计算模型

【例1-3】设计算法，输出一个n×n的三角矩阵，如图所示规律。

【1-5】运用递归方式设计求解斐波那契数列(Fibonacci sequence)的第n项的值

计算模型

算法分析

3.循环与递归的比较

【例1-5】任意给定十进制数：(1)从低位到高位逐位输出各位数字; (2) 从高位到低位逐位输出各位数字。

问题分析

算法实现

【例1-6】求从n个自然数(1,2,3,…, n)中取出r个数的所有组合。

计算模型：1）循环算法：

2）递归

算法实现

【1-7】找出n个自然数(1,2,3,…, n)中取出r个数的所有组合。

算法分析

算法设计与描述

比较总结：

1. 循环设计

(1) 设计思维

自底向上的设计（Down - Top Design）

先找出某个问题的子问题或若干特殊问题，

以定性、定量的方式去描述和解决这些子问题，

然后，逐步合并子问题的解，最后得到大问题的解。

核心本质：合并

自顶向下的设计（Top-Down Design）

将复杂的大问题分解为相对简单的小问题，

找出每个问题的关键、重点所在，

然后用精确的思维定性、定量地去描述问题和解决问题。

核心本质：分解。

例如：归并算法：自顶向下拆，自底向上合并

(2)挖掘内在规律构建计算模型

挖掘问题的内在规律，进行抽象并构建计算模型

交通指挥灯：数据构造

三角矩阵：运算规律

运算规律：一般找下标对应规律最快

【例1-3】设计算法，输出一个n×n的三角矩阵，如图所示规律。

行列参与运算（下标）

问题分析：

问题：要找到按斜行访问与按矩阵访问之间的映射关系？

计算模型：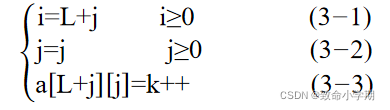

算法设计与描述：

输入：矩阵行列值n

输出：按斜行元素值为连续整数的三角矩阵

算法分析：

算法主体语句执行次数为：

其中，L代表斜行，j代表列。

【其实是每一个元素都进行操作，且只进行一次。所以执行次数=元素个数】

【第一斜行n 第二斜行......】

算法实现：

#include<stdio.h>

int main()
{
	// 输入  
	int n,k=1;
	int a[100][100];
	printf("请输入n值：");
	scanf("%d",&n);
	
	for(int L=0;L<n;L++)//L是斜行 
	{
		for(int j=0;j<n-L ;j++)
		{
			a[L+j][j] = k++ ;
		}
	}
	//输出
	for(int i=0;i<n;i++)
	{
		for(int j=0;j<=i;j++)
		{
			printf("%5d",a[i][j]);
		}
		printf("\n");
	} 
	return 0;
}

思考题：n=5*5?

代码：

#include<iostream>
using namespace std;

int main()
{
	int n=5*5;
	int k=0;
	int a[n][n];
	for (int i=0;i<n;i++)
	{
		for(int j=0;j<n-i;j++)
		{
			a[i+j][j]=k++;
		}
	}
	for(int i=0;i<n;i++)
	{
		for(int j=0;j<=i;j++)//注意这里是<= 
		{