算法日记-07数组进阶篇

数组进阶篇

977. 有序数组的平方

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

示例 1：

输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]

示例 2：

输入：nums = [-7,-3,2,3,11]
输出：[4,9,9,49,121]

解题思路

本题求解的数组中每个元素平方后的数组，然后按从小到大的顺序排列

使用Java语言的同学，我们可以先对数组中的每个值平方运算后，调用Arrays.sort()方法进行排序。正常情况下若第一个元素是大于等于0的那么数组取平方后就是我们的答案，若第一个元素是负数，那么我们该考虑到要从头和尾同时进行判断，找出最大的值，那么结果数组的最后一位就是最大的值，所以我们应该联想到双指针法，用头尾指针进行遍历，数组的赋值我们则从后往前。

实现代码

排序解法

class Solution {
    public int[] sortedSquares(int[] nums) {
        for(int i=0;i<nums.length;i++){
            nums[i] = nums[i]*nums[i];
        }
        Arrays.sort(nums);
        return nums;
    }
}

双指针法

class Solution {
    public int[] sortedSquares(int[] nums) {
        int left = 0;
        int right = nums.length-1;
        int[] result = new int[nums.length];
        int num = result.length-1;
        while(left<=right){
            if(nums[left]*nums[left] < nums[right]*nums[right]){
                result[num] = nums[right]*nums[right];
                right--;
                num--;
            }else{
                result[num] = nums[left]*nums[left];
                left++;
                num--;
            }
        }
        return result;
    }
}

209. 长度最小的子数组

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度**。**如果不存在符合条件的子数组，返回 0 。

示例 1：

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：

输入：target = 4, nums = [1,4,4]
输出：1

示例 3：

输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

解题思路

本题题意是求出满足其总和大于等于 target 的长度最小的 连续子数组，那么我们需要先找出总和大于target的的连续子数组，然后记录其数组长度，最后输出长度最小的连续子数组。那么我们该如何求出长度最小的连续子数组呢，我们可以使用滑动窗口来解决这个问题，

每当我们遍历一个值，就将其加入我们的滑动窗口，当滑动窗口中的值大于target时说明我们找到了一个满足条件的连续子数组，这时我们从数组的左边不断缩短他的长度，若缩减后依然满足条件则继续缩减，若不满足条件后，我们则需要继续遍历数组将新遍历的值不断加入滑动窗口中，重复此操作知道遍历完数组的最后一个值。

实现代码

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int left = 0;
        int sum = 0;
        int n = Integer.MAX_VALUE;
        for(int right=0;right<nums.length;right++){
            sum += nums[right];
            //说明滑动窗口此时满足条件
            while(sum>=target){
                int len = right-left+1;
                n = Math.min(n,len);
                sum -= nums[left];
                left++;
            }
        }
        return n==Integer.MAX_VALUE?0:n;
    }
}

59. 螺旋矩阵 II

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1：

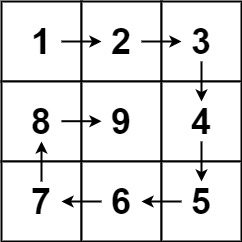
输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

示例 2：

输入：n = 1
输出：[[1]]

解题思路

本题的主要难点实际上就在于我们对数组的掌握情况，以及对边界理解，到底是左闭右开还是左闭右闭一定要思考清楚。

本题难点，我们需要用变量loop来记录要循环的圈数，当loop<n/2时 我们就进入遍历，每次遍历让loop++，遍历顺序我们选择顺时针转圈填充，定义一个start变量用于记录我们每次开始遍历的位置，当遍历完一圈后让start++，下一次进入遍历将从内圈开始。

当n为奇数即 n%2==1时 我们需要额外对数组中心进行填充

result[n/2][n/2] = n*n;

实现代码

class Solution {
    public int[][] generateMatrix(int n) {
        int[][] result = new int[n][n];
        int loop = 0;//控制循环次数 一共需要填充loop<n/2圈
        int start = 0;
        int num = 1;
        int i,j;
        while(loop++<n/2){
            //左上角到右上角
            for(i=start;i<n-loop;i++){
                result[start][i] = num;
                num++;
            }
            //右上角到右下角
            for(j=start;j<n-loop;j++){
                result[j][i] = num;
                num++;
            }
            //从右下角到左下角
            for(;i>=loop;i--){
                result[j][i] = num;
                num++;
            }
            //从左下角到左上角
            for(;j>=loop;j--){
                result[j][i] = num;
                num++;
            }
            start++;
        }
        if(n%2==1){
            result[n/2][n/2] = n*n;
        }
        return result;
    }
}

//从右下角到左下角
for(;i>=loop;i–){
result[j][i] = num;
num++;
}
//从左下角到左上角
for(;j>=loop;j–){
result[j][i] = num;
num++;
}
start++;
}
if(n%2==1){
result[n/2][n/2] = n*n;
}
return result;
}
}