让微积分穿梭于工作与学习之间（15）：圆弧直线的圆心，半径及其在趋于直线时的极限

从本篇开始，我会开始给大家分享微积分在CAD圆弧直线中的应用。

对CAD圆弧直线不了解的朋友可以先阅读以下博文：

https://blog.csdn.net/iloveas2014/article/details/103837857

https://blog.csdn.net/iloveas2014/article/details/103848611

考虑到本篇是第一篇，我把上文用到的动图也给出来。

图中，S和E是已知的两个点，然后bulge为凸度，它等于圆心角1/4的正切值。即

bulge=tan(α/4)

不难发现，在这种曲线中，从圆弧到直线，最大的一个质变是圆心没了，但如果站在极限的角度去理解，那我们可以说圆心是跑到了无穷大的地方。

在此先说明一下，bulge是个有符号的值，不等于0时，为正时代表从起点到终点是沿着正方向走（在y轴向上的坐标系是逆时针），否则为负方向。

下面我们先根据这种曲线的定义把圆心的坐标给算出来。

曾经我很讨厌解析几何教材中椭圆，双曲线等章节，因为它们把焦点都固定在了坐标轴上，并且关于原点对称，导致方程显得很不通用。但如今我也打算沿用这样的方式，如果点的坐标没有任何约束的话，那演算过程将会变得非常繁琐，看得头晕的同时也不便于研究其特性。

所以我的计划是，在开始探讨某个性质的时候，我会尽可能把一些条件的值给写死得简单点，到后面再尝试给出一般情况的公式。

如图，我把圆弧直线的两个端点S，E放在一个很对称的位置，并且都在x轴上。

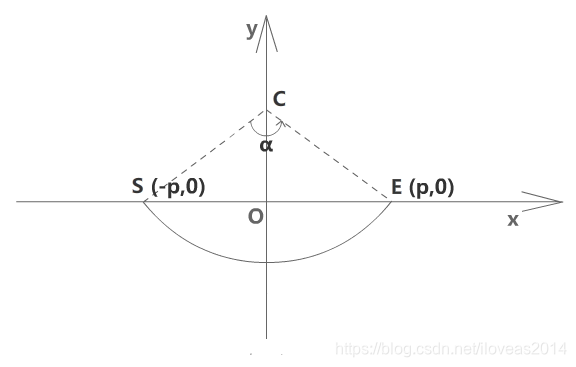
然后，α为圆弧的圆心角，因此根据定义，有bulge=tan(α/4)

接着，圆弧的圆心为C，其x坐标一定为0，然后通过直角三角形SOC可算出y坐标等于

cy=OC=OS*cot∠SCO=OScot(α/2)=pcot(α/2)。

然后我们知道α不是直接的已知条件，我们化成用bulge表示的形式（以下简写为b）

首先算出角度α

接着代入得到

这式子虽然看着不复杂，但可操作性却非常差，如此简短的一个表达式同时包含了三角函数和反三角函数，对于后续的处理将变得非常不便，为此我们想办法把它给化开。

首先正切和反正切互为反函数

然后正切和余切互为倒数

因此我们可以把上面的余切变成正切然后用二倍角公式展开，看能不能简化一些。

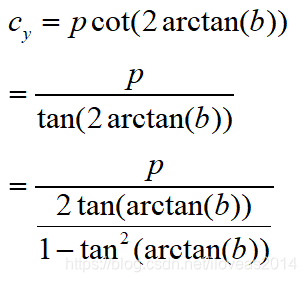
看起来好使，全变成了可以相互抵消的反函数。

嗯现在圆心的y坐标非常精简了，然后x坐标恒等于0。

在本课题研究极限的过程中，p为常量，所以上述的式子是一个以b为自变量（ 此处以大于0的区间为例），cy为因变量的函数，其导数值为

可见这是一个单调递减函数，也就是说，当bulge从大于0到趋于0的过程中，函数值逐渐增加，而当b趋于0时，有

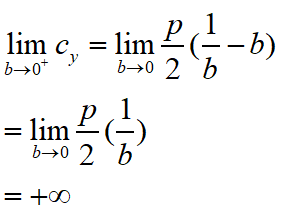
也就是说，b从大于0趋于0的过程中，圆心会沿着y轴正方向越跑越远，并且没有上限。

然后我们来研究下它的半径。

 

图中的SC或者CE都代表这段弧的半径。显然SO(p)和SC的关系是对边和斜边的关系，于是有

R=SC=SO/sin(α/2)=SOcsc(α/2)=pcsc(α/2)

余割和余切之间存在跟正余弦平方等于1相类似的恒等关系

于是我们可以这样化简。

此处余切值的变换用到了前面推导的结果，如果觉得跳跃大了的话就可以重温下上面算圆心的部分。

虽然圆心跟半径的差别仅仅是一次项的符号，但它在正实数区间不是单调函数，而是在b=1处有极值点。因为

令

得到

取正的解，得到b=1，也就是说，凸度等于1，也就是刚好半圆的时候，半径可以取得最小值（b<1时导数小于0，b>1时导数大于0）。

半径在半圆时取得最小值可以拿个图形象地说明下的，但是由于半径的单调性不是本课题的重点，所以就懒得做了。有兴趣的朋友可以自己画几个图体会一下。此处只给出静态图，说明bulge=1时斜边SC和直角边SO重合，斜边取得最小值。

然后同样地，在b趋于0时，半径一样趋于无穷大。

圆心和半径都趋于无穷大，这对于一般的编程语言来说都是不好表示的。

当然了，当圆弧变为直线的时候，我们更多的是希望更多跟圆心半径没有直接关系的一些变量可以跟圆弧共用一套算法来进行规划和实现而非通过if来进行区分。这个时候，我们就要运用更多的极限乃至微积分知识来把圆弧和直线的计算方法给统一起来。那具体都有些什么呢？我会在后续的连载中给大家一一讲解，敬请期待！