1.气隙的概念
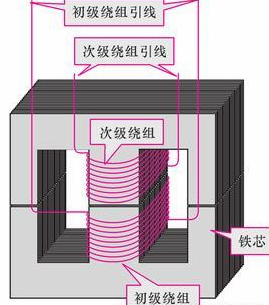
首先来看看EE变压器的结构
制作变压器时,首先准备一个骨架

将电磁线缠绕上去

绝缘后插上EE磁芯,再固定住和加外壳

气隙:为了防止变压器磁饱和而对磁芯开出的空隙
(在下图中,两个E中间的那条缝隙即为气隙)
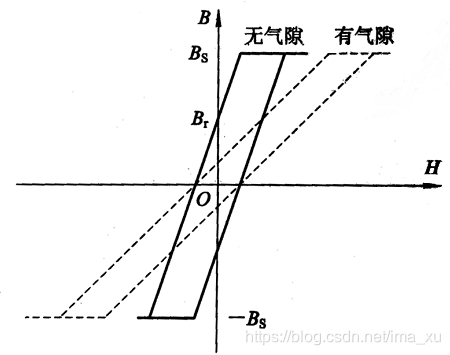
根据电磁学的知识,磁芯的磁场变化具有滞后性,即呈现出下图中分别的两条磁滞回线
由于
B
=
μ
×
H
B = \mu × H
B=μ×H,开了气隙后,由于一部分磁芯的
μ
r
\mu_r
μr变成了
μ
0
\mu_0
μ0(空气中的磁导率),总磁导率
μ
\mu
μ会变小,即斜率变小。
这就使得磁饱和时(B为最大/最小值)对应的磁场强度H更大,即电感电流更大(意味着电路升降压的性能越好)
一般来说,气隙的理想开口位置如下

2.磁芯的影响
由笔记4的公式
N
×
A
e
×
μ
Δ
H
=
L
×
Δ
I
N × A_{e} × \mu\Delta H = L × \Delta I
N×Ae×μΔH=L×ΔI(电磁感应定律)
H
×
L
e
=
N
×
I
H× L_{e} = N ×I
H×Le=N×I(安培环路定律)
可求得,无气隙磁芯的电感量为
- L = N 2 μ A e l e L = \frac{N^2\mu A_e}{l_e} L=leN2μAe ①

此处引入三个常用概念
- 电感系数 A L = μ A e l e A_L = \frac{\mu A_e}{l_e} AL=leμAe ②
- 磁芯磁阻 R C = 1 A L = l e μ A e R_C = \frac{1}{A_L} = \frac{l_e}{\mu A_e} RC=AL1=μAele ③
- 磁芯常数 C 1 = l e A e C_1 = \frac{l_e}{A_e} C1=Aele ④
②代入①,得:
L
=
N
2
A
L
L = N^2A_L
L=N2AL ⑤
④代入②,得:
μ
=
C
1
A
L
\mu = C_1A_L
μ=C1AL ⑥
由式⑥可知, A L A_L AL不变时 C 1 C_1 C1增大,会导致 μ \mu μ增大
而在电感的体积公式(笔记6)中可知,其它量不变时, μ \mu μ增大会导致电压体积增大。
所以应选用 C 1 C_1 C1小一点的磁芯
由式⑤可知,确定好设计中的电感量L时,若减小 A L A_L AL,对应的匝数N就会变多,这将使得工艺难度增加而且线圈损耗增加。所以设计中 A L A_L AL应取大一些
但是由公式⑥可知, A L A_L AL增大会导致 μ \mu μ增大,即电感体积增大,这时可以通过减小 C 1 C_1 C1来保持电感体积
3.气隙的计算
一般来说,机器制作时气隙长度可以较准确地开出,而手工磨磁芯就变得不可控了(难以测量),事实上,在开关电源的研发过程中,机器量产前都是靠手工磨磁芯。这时,就得依靠其它变量来推知所磨磁芯的气隙长度

当气隙长度
δ
\delta
δ较大时,我们可近似认为气隙界面向外扩展了气隙长度
δ
\delta
δ
假设是圆截面磁芯,气隙截面半径 = 磁芯截面半径 +
δ
\delta
δ
假设是正方形截面磁芯,气隙截面边长= 磁芯截面边长 +
δ
\delta
δ
气隙计算公式1
磁芯磁阻为
R
m
=
R
C
+
R
δ
=
l
e
−
δ
μ
r
μ
0
A
e
+
δ
μ
0
A
δ
R_m = R_C + R_\delta = \frac{l_e - \delta}{\mu_r\mu_0 A_e} + \frac{\delta}{\mu_0 A_\delta}
Rm=RC+Rδ=μrμ0Aele−δ+μ0Aδδ
当
R
δ
≫
R
C
R_\delta \gg R_C
Rδ≫RC,即
μ
r
\mu_r
μr或者
δ
\delta
δ很大时,可忽略
R
C
R_C
RC
代入式
L
=
N
2
R
m
L = \frac{N^2}{R_m}
L=RmN2得:
δ ≈ μ 0 A δ N 2 L \delta \approx \mu_0A_\delta\frac{N^2}{L} δ≈μ0AδLN2
该公式用来估算出的气隙值精度很低,一般不使用
气隙计算公式2
当
δ
≪
l
e
\delta \ll l_e
δ≪le时
L
=
N
2
R
m
=
N
2
l
e
−
δ
μ
r
μ
0
A
e
+
δ
μ
0
A
δ
=
N
2
l
e
μ
r
μ
0
A
e
+
δ
μ
0
A
δ
=
N
2
1
A
L
+
δ
μ
0
A
δ
L = \frac{N^2}{R_m} = \frac{N^2}{\frac{l_e - \delta}{\mu_r\mu_0 A_e} + \frac{\delta}{\mu_0 A_\delta}} = \frac{N^2}{\frac{l_e}{\mu_r\mu_0 A_e} + \frac{\delta}{\mu_0 A_\delta}} = \frac{N^2}{\frac{1}{A_L} + \frac{\delta}{\mu_0 A_\delta}}
L=RmN2=μrμ0Aele−δ+μ0AδδN2=μrμ0Aele+μ0AδδN2=AL1+μ0AδδN2
即:
δ = μ 0 A δ ( N 2 L − 1 A L ) \delta = \mu_0A_\delta(\frac{N^2}{L} - \frac{1}{A_L}) δ=μ0Aδ(LN2−AL1)
该式的计算精度最高
气隙计算公式3
当气隙长度
δ
\delta
δ 较小时(相比于横截面的半径/边长)
可近似认为
A
δ
=
A
e
A_\delta = A_e
Aδ=Ae
即
δ = μ 0 A e ( N 2 L − 1 A L ) \delta = \mu_0A_e(\frac{N^2}{L} - \frac{1}{A_L}) δ=μ0Ae(LN2−AL1)
实际使用中,其实不需要计算出电感系数
A
L
A_L
AL
在开始磨磁芯前(无气隙
δ
0
=
0
\delta_0 = 0
δ0=0),先测出当前电感值
L
0
L_0
L0;磨完磁芯后,再测出电感值
L
L
L
Δ
δ
=
δ
=
μ
0
A
e
(
N
2
L
−
N
2
L
0
)
\Delta\delta = \delta = \mu_0A_e(\frac{N^2}{L} - \frac{N^2}{L_0})
Δδ=δ=μ0Ae(LN2−L0N2)
























 868
868

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








