转自著名的“丕子”博客
在统计计算中,最大期望(EM)算法是在概率(probabilistic)模型中寻找参数最大似然估计的算法,其中概率模型依赖于无法观测的隐藏变量(Latent Variable)。最大期望经常用在机器学习和计算机视觉的数据聚类(Data Clustering) 领域。最大期望算法经过两个步骤交替进行计算,第一步是计算期望(E),利用对隐藏变量的现有估计值,计算其最大似然估计值;第二步是最大化(M),最大 化在 E 步上求得的最大似然值来计算参数的值。M 步上找到的参数估计值被用于下一个 E 步计算中,这个过程不断交替进行。
最大期望值算法由 Arthur Dempster,Nan Laird和Donald Rubin在他们1977年发表的经典论文中提出。他们指出此方法之前其实已经被很多作者"在他们特定的研究领域中多次提出过"。
我们用 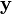 表示能够观察到的不完整的变量值,用
表示能够观察到的不完整的变量值,用  表示无法观察到的变量值,这样
表示无法观察到的变量值,这样  和
和 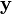 一起组成了完整的数据。
一起组成了完整的数据。 可能是实际测量丢失的数据,也可能是能够简化问题的隐藏变量,如果它的值能够知道的话。例如,在混合模型(Mixture Model)中,如果“产生”样本的混合元素成分已知的话最大似然公式将变得更加便利(参见下面的例子)。
可能是实际测量丢失的数据,也可能是能够简化问题的隐藏变量,如果它的值能够知道的话。例如,在混合模型(Mixture Model)中,如果“产生”样本的混合元素成分已知的话最大似然公式将变得更加便利(参见下面的例子)。
估计无法观测的数据
让  代表矢量 θ:
代表矢量 θ: 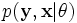 定义的参数的全部数据的概率分布(连续情况下)或者概率聚类函数(离散情况下),那么从这个函数就可以得到全部数据的最大似然值,另外,在给定的观察到的数据条件下未知数据的条件分布可以表示为:
定义的参数的全部数据的概率分布(连续情况下)或者概率聚类函数(离散情况下),那么从这个函数就可以得到全部数据的最大似然值,另外,在给定的观察到的数据条件下未知数据的条件分布可以表示为:
EM算法有这么两个步骤E和M:
-
Expectation step: Choose
q to maximize
F:
-
-
Maximization step: Choose
θ to maximize
F:
-
举个例子吧:高斯混合
假设 x = (x1,x2,…,xn) 是一个独立的观测样本,来自两个多元d维正态分布的混合, 让z=(z1,z2,…,zn)是潜在变量,确定其中的组成部分,是观测的来源.
即:
-
 and
and

where
-
 and
and

目标呢就是估计下面这些参数了,包括混合的参数以及高斯的均值很方差:
似然函数:
where  是一个指示函数 ,f 是 一个多元正态分布的概率密度函数. 可以写成指数形式:
是一个指示函数 ,f 是 一个多元正态分布的概率密度函数. 可以写成指数形式:
下面就进入两个大步骤了:
E-step
给定目前的参数估计 θ(t), Zi 的条件概率分布是由贝叶斯理论得出,高斯之间用参数 τ加权:
-
 .
.
因此,E步骤的结果:
M步骤
Q(θ|θ(t))的二次型表示可以使得 最大化θ相对简单. τ, (μ1,Σ1) and (μ2,Σ2) 可以单独的进行最大化.
首先考虑 τ, 有条件τ1 + τ2=1:
和MLE的形式是类似的,二项分布 , 因此:
下一步估计 (μ1,Σ1):
和加权的 MLE就正态分布来说类似
-
 and
and

对称的:
-
 and
and
 .
.
这个例子来自Answers.com的Expectation-maximization algorithm,由于还没有深入体验,心里还说不出一些更通俗易懂的东西来,等研究了并且应用了可能就有所理解和消化。另外,liuxqsmile也做了一些理解和翻译。
============
在网上的源码不多,有一个很好的EM_GM.m,是滑铁卢大学的Patrick P. C. Tsui写的,拿来分享一下:
运行的时候可以如下进行初始化:
|
1
2
3
4
5
|
X = zeros(600,2);
X(1:200,:) = normrnd(0,1,200,2);
X(201:400,:) = normrnd(0,2,200,2);
X(401:600,:) = normrnd(0,3,200,2);
[W,M,V,L] = EM_GM(X,3,[],[],1,[])
|
下面是程序源码:
|
001
002
003
004
005
006
007
008
009
010
011
012
013
014
015
016
017
018
019
020
021
022
023
024
025
026
027
028
029
030
031
032
033
034
035
036
037
038
039
040
041
042
043
044
045
046
047
048
049
050
051
052
053
054
055
056
057
058
059
060
061
062
063
064
065
066
067
068
069
070
071
072
073
074
075
076
077
078
079
080
081
082
083
084
085
086
087
088
089
090
091
092
093
094
095
096
097
098
099
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
|
function
[W,M,V,L] = EM_GM(X,k,ltol,maxiter,pflag,Init)
% [W,M,V,L] = EM_GM(X,k,ltol,maxiter,pflag,Init)
%
% EM algorithm for k multidimensional Gaussian mixture estimation
%
% Inputs:
% X(n,d) - input data, n=number of observations, d=dimension of variable
% k - maximum number of Gaussian components allowed
% ltol - percentage of the log likelihood difference between 2 iterations ([] for none)
% maxiter - maximum number of iteration allowed ([] for none)
% pflag - 1 for plotting GM for 1D or 2D cases only, 0 otherwise ([] for none)
% Init - structure of initial W, M, V: Init.W, Init.M, Init.V ([] for none)
%
% Ouputs:
% W(1,k) - estimated weights of GM
% M(d,k) - estimated mean vectors of GM
% V(d,d,k) - estimated covariance matrices of GM
% L - log likelihood of estimates
%
% Written by
% Patrick P. C. Tsui,
% PAMI research group
% Department of Electrical and Computer Engineering
% University of Waterloo,
% March, 2006
%
%%%% Validate inputs %%%%
if
nargin <= 1,
disp(
'EM_GM must have at least 2 inputs: X,k!/n'
)
return
elseif
nargin == 2,
ltol = 0.1; maxiter = 1000; pflag = 0; Init = [];
err_X = Verify_X(X);
err_k = Verify_k(k);
if
err_X | err_k,
return
;
end
elseif
nargin == 3,
maxiter = 1000; pflag = 0; Init = [];
err_X = Verify_X(X);
err_k = Verify_k(k);
[ltol,err_ltol] = Verify_ltol(ltol);
if
err_X | err_k | err_ltol,
return
;
end
elseif
nargin == 4,
pflag = 0; Init = [];
err_X = Verify_X(X);
err_k = Verify_k(k);
[ltol,err_ltol] = Verify_ltol(ltol);
[maxiter,err_maxiter] = Verify_maxiter(maxiter);
if
err_X | err_k | err_ltol | err_maxiter,
return
;
end
elseif
nargin == 5,
Init = [];
err_X = Verify_X(X);
err_k = Verify_k(k);
[ltol,err_ltol] = Verify_ltol(ltol);
[maxiter,err_maxiter] = Verify_maxiter(maxiter);
[pflag,err_pflag] = Verify_pflag(pflag);
if
err_X | err_k | err_ltol | err_maxiter | err_pflag,
return
;
end
elseif
nargin == 6,
err_X = Verify_X(X);
err_k = Verify_k(k);
[ltol,err_ltol] = Verify_ltol(ltol);
[maxiter,err_maxiter] = Verify_maxiter(maxiter);
[pflag,err_pflag] = Verify_pflag(pflag);
[Init,err_Init]=Verify_Init(Init);
if
err_X | err_k | err_ltol | err_maxiter | err_pflag | err_Init,
return
;
end
else
disp(
'EM_GM must have 2 to 6 inputs!'
);
return
end
%%%% Initialize W, M, V,L %%%%
t = cputime;
if
isempty(Init),
[W,M,V] = Init_EM(X,k); L = 0;
else
W = Init.W;
M = Init.M;
V = Init.V;
end
Ln = Likelihood(X,k,W,M,V);
% Initialize log likelihood
Lo = 2*Ln;
%%%% EM algorithm %%%%
niter = 0;
while
(abs(100*(Ln-Lo)/Lo)>ltol) & (niter<=maxiter),
E = Expectation(X,k,W,M,V);
% E-step
[W,M,V] = Maximization(X,k,E);
% M-step
Lo = Ln;
Ln = Likelihood(X,k,W,M,V);
niter = niter + 1;
end
L = Ln;
%%%% Plot 1D or 2D %%%%
if
pflag==1,
[n,d] = size(X);
if
d>2,
disp(
'Can only plot 1 or 2 dimensional applications!/n'
);
else
Plot_GM(X,k,W,M,V);
end
elapsed_time = sprintf(
'CPU time used for EM_GM: %5.2fs'
,cputime-t);
disp(elapsed_time);
disp(sprintf(
'Number of iterations: %d'
,niter-1));
end
%%%%%%%%%%%%%%%%%%%%%%
%%%% End of EM_GM %%%%
%%%%%%%%%%%%%%%%%%%%%%
function
E = Expectation(X,k,W,M,V)
[n,d] = size(X);
a = (2*pi)^(0.5*d);
S = zeros(1,k);
iV = zeros(d,d,k);
for
j=1:k,
if
V(:,:,j)==zeros(d,d), V(:,:,j)=ones(d,d)*eps;
end
S(j) = sqrt(det(V(:,:,j)));
iV(:,:,j) = inv(V(:,:,j));
end
E = zeros(n,k);
for
i=1:n,
for
j=1:k,
dXM = X(i,:)'-M(:,j);
pl = exp(-0.5*dXM'*iV(:,:,j)*dXM)/(a*S(j));
E(i,j) = W(j)*pl;
end
E(i,:) = E(i,:)/sum(E(i,:));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%% End of Expectation %%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function
[W,M,V] = Maximization(X,k,E)
[n,d] = size(X);
W = zeros(1,k); M = zeros(d,k);
V = zeros(d,d,k);
for
i=1:k,
% Compute weights
for
j=1:n,
W(i) = W(i) + E(j,i);
M(:,i) = M(:,i) + E(j,i)*X(j,:)';
end
M(:,i) = M(:,i)/W(i);
end
for
i=1:k,
for
j=1:n,
dXM = X(j,:)'-M(:,i);
V(:,:,i) = V(:,:,i) + E(j,i)*dXM*dXM';
end
V(:,:,i) = V(:,:,i)/W(i);
end
W = W/n;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%% End of Maximization %%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function
L = Likelihood(X,k,W,M,V)
% Compute L based on K. V. Mardia, "Multivariate Analysis", Academic Press, 1979, PP. 96-97
% to enchance computational speed
[n,d] = size(X);
U = mean(X)';
S = cov(X);
L = 0;
for
i=1:k,
iV = inv(V(:,:,i));
L = L + W(i)*(-0.5*n*log(det(2*pi*V(:,:,i))) ...
-0.5*(n-1)*(trace(iV*S)+(U-M(:,i))'*iV*(U-M(:,i))));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%% End of Likelihood %%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%
function
err_X = Verify_X(X)
err_X = 1;
[n,d] = size(X);
if
n<d,
disp(
'Input data must be n x d!/n'
);
return
end
err_X = 0;
%%%%%%%%%%%%%%%%%%%%%%%%%
%%%% End of Verify_X %%%%
%%%%%%%%%%%%%%%%%%%%%%%%%
function
err_k = Verify_k(k)
err_k = 1;
if
~isnumeric(k) | ~isreal(k) | k<1,
disp(
'k must be a real integer >= 1!/n'
);
return
end
err_k = 0;
%%%%%%%%%%%%%%%%%%%%%%%%%
%%%% End of Verify_k %%%%
%%%%%%%%%%%%%%%%%%%%%%%%%
function
[ltol,err_ltol] = Verify_ltol(ltol)
err_ltol = 1;
if
isempty(ltol),
ltol = 0.1;
elseif
~isreal(ltol) | ltol<=0,
disp(
'ltol must be a positive real number!'
);
return
end
err_ltol = 0;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%% End of Verify_ltol %%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function
[maxiter,err_maxiter] = Verify_maxiter(maxiter)
err_maxiter = 1;
if
isempty(maxiter),
maxiter = 1000;
elseif
~isreal(maxiter) | maxiter<=0,
disp(
'ltol must be a positive real number!'
);
return
end
err_maxiter = 0;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%% End of Verify_maxiter %%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function
[pflag,err_pflag] = Verify_pflag(pflag)
err_pflag = 1;
if
isempty(pflag),
pflag = 0;
elseif
pflag~=0 & pflag~=1,
disp(
'Plot flag must be either 0 or 1!/n'
);
return
end
err_pflag = 0;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%% End of Verify_pflag %%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function
[Init,err_Init] = Verify_Init(Init)
err_Init = 1;
if
isempty(Init),
% Do nothing;
elseif
isstruct(Init),
[Wd,Wk] = size(Init.W);
[Md,Mk] = size(Init.M);
[Vd1,Vd2,Vk] = size(Init.V);
if
Wk~=Mk | Wk~=Vk | Mk~=Vk,
disp(
'k in Init.W(1,k), Init.M(d,k) and Init.V(d,d,k) must equal!/n'
)
return
end
if
Md~=Vd1 | Md~=Vd2 | Vd1~=Vd2,
disp(
'd in Init.W(1,k), Init.M(d,k) and Init.V(d,d,k) must equal!/n'
)
return
end
else
disp(
'Init must be a structure: W(1,k), M(d,k), V(d,d,k) or []!'
);
return
end
err_Init = 0;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%% End of Verify_Init %%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function
[W,M,V] = Init_EM(X,k)
[n,d] = size(X);
[Ci,C] = kmeans(X,k,
'Start'
,
'cluster'
, ...
'Maxiter'
,100, ...
'EmptyAction'
,
'drop'
, ...
'Display'
,
'off'
);
% Ci(nx1) - cluster indeices; C(k,d) - cluster centroid (i.e. mean)
while
sum(isnan(C))>0,
[Ci,C] = kmeans(X,k,
'Start'
,
'cluster'
, ...
'Maxiter'
,100, ...
'EmptyAction'
,
'drop'
, ...
'Display'
,
'off'
);
end
M = C';
Vp = repmat(struct(
'count'
,0,
'X'
,zeros(n,d)),1,k);
for
i=1:n,
% Separate cluster points
Vp(Ci(i)).count = Vp(Ci(i)).count + 1;
Vp(Ci(i)).X(Vp(Ci(i)).count,:) = X(i,:);
end
V = zeros(d,d,k);
for
i=1:k,
W(i) = Vp(i).count/n;
V(:,:,i) = cov(Vp(i).X(1:Vp(i).count,:));
end
%%%%%%%%%%%%%%%%%%%%%%%%
%%%% End of Init_EM %%%%
%%%%%%%%%%%%%%%%%%%%%%%%
function
Plot_GM(X,k,W,M,V)
[n,d] = size(X);
if
d>2,
disp(
'Can only plot 1 or 2 dimensional applications!/n'
);
return
end
S = zeros(d,k);
R1 = zeros(d,k);
R2 = zeros(d,k);
for
i=1:k,
% Determine plot range as 4 x standard deviations
S(:,i) = sqrt(diag(V(:,:,i)));
R1(:,i) = M(:,i)-4*S(:,i);
R2(:,i) = M(:,i)+4*S(:,i);
end
Rmin = min(min(R1));
Rmax = max(max(R2));
R = [Rmin:0.001*(Rmax-Rmin):Rmax];
clf, hold on
if
d==1,
Q = zeros(size(R));
for
i=1:k,
P = W(i)*normpdf(R,M(:,i),sqrt(V(:,:,i)));
Q = Q + P;
plot(R,P,
'r-'
); grid on,
end
plot(R,Q,
'k-'
);
xlabel(
'X'
);
ylabel(
'Probability density'
);
else
% d==2
plot(X(:,1),X(:,2),
'r.'
);
for
i=1:k,
Plot_Std_Ellipse(M(:,i),V(:,:,i));
end
xlabel(
'1^{st} dimension'
);
ylabel(
'2^{nd} dimension'
);
axis([Rmin Rmax Rmin Rmax])
end
title(
'Gaussian Mixture estimated by EM'
);
%%%%%%%%%%%%%%%%%%%%%%%%
%%%% End of Plot_GM %%%%
%%%%%%%%%%%%%%%%%%%%%%%%
function
Plot_Std_Ellipse(M,V)
[Ev,D] = eig(V);
d = length(M);
if
V(:,:)==zeros(d,d),
V(:,:) = ones(d,d)*eps;
end
iV = inv(V);
% Find the larger projection
P = [1,0;0,0];
% X-axis projection operator
P1 = P * 2*sqrt(D(1,1)) * Ev(:,1);
P2 = P * 2*sqrt(D(2,2)) * Ev(:,2);
if
abs(P1(1)) >= abs(P2(1)),
Plen = P1(1);
else
Plen = P2(1);
end
count = 1;
step = 0.001*Plen;
Contour1 = zeros(2001,2);
Contour2 = zeros(2001,2);
for
x = -Plen:step:Plen,
a = iV(2,2);
b = x * (iV(1,2)+iV(2,1));
c = (x^2) * iV(1,1) - 1;
Root1 = (-b + sqrt(b^2 - 4*a*c))/(2*a);
Root2 = (-b - sqrt(b^2 - 4*a*c))/(2*a);
if
isreal(Root1),
Contour1(count,:) = [x,Root1] + M';
Contour2(count,:) = [x,Root2] + M';
count = count + 1;
end
end
Contour1 = Contour1(1:count-1,:);
Contour2 = [Contour1(1,:);Contour2(1:count-1,:);Contour1(count-1,:)];
plot(M(1),M(2),
'k+'
);
plot(Contour1(:,1),Contour1(:,2),
'k-'
);
plot(Contour2(:,1),Contour2(:,2),
'k-'
);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%% End of Plot_Std_Ellipse %%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
|








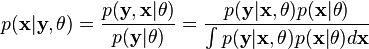




![L(\theta;\mathbf{x},\mathbf{z}) = \exp \left\{ \sum_{i=1}^n \sum_{j=1}^2 \mathbb{I}(z_i=j) \big[ \log \tau_j -\tfrac{1}{2} \log |\Sigma_j| -\tfrac{1}{2}(\mathbf{x}_i-\boldsymbol{\mu}_j)^\top\Sigma_j^{-1} (\mathbf{x}_i-\boldsymbol{\mu}_j) -\tfrac{d}{2} \log(2\pi) \big] \right\}](http://wpcontent.answcdn.com/math/d/5/3/d53e50b61c8d3465b6bd20e085933f6a.png)
![\begin{align}Q(\theta|\theta^{(t)}) &= \operatorname{E} [\log L(\theta;\mathbf{x},\mathbf{Z}) ] \\ &= \sum_{i=1}^n \sum_{j=1}^2 T_{j,i}^{(t)} \big[ \log \tau_j -\tfrac{1}{2} \log |\Sigma_j| -\tfrac{1}{2}(\mathbf{x}_i-\boldsymbol{\mu}_j)^\top\Sigma_j^{-1} (\mathbf{x}_i-\boldsymbol{\mu}_j) -\tfrac{d}{2} \log(2\pi) \big] \end{align}](http://wpcontent.answcdn.com/math/8/4/e/84efae4d173871c8ffb2f53a0c67595f.png)
![\begin{align}\boldsymbol{\tau}^{(t+1)} &= \underset{\boldsymbol{\tau}} \operatorname{arg\,max}\ Q(\theta | \theta^{(t)} ) \\ &= \underset{\boldsymbol{\tau}} \operatorname{arg\,max} \ \left\{ \left[ \sum_{i=1}^n T_{1,i}^{(t)} \right] \log \tau_1 + \left[ \sum_{i=1}^n T_{2,i}^{(t)} \right] \log \tau_2 \right\} \end{align}](http://wpcontent.answcdn.com/math/d/c/8/dc83eff0611209a985b5671d8059f072.png)
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








