算法系列之九：计算几何与图形学有关的几种常用算法（一）

   我的专业是计算机辅助设计（CAD），算是一半机械一半软件，《计算机图形学》是必修课，也是我最喜欢的课程。热衷于用代码摆平一切的我几乎将这本教科书上的每种算法都实现了一遍，这种重复劳动虽然意义不大，但是收获很多，特别是丢弃了多年的数学又重新回到了脑袋中，算是最大的收获吧。尽管已经毕业多年了，但是每次回顾这些算法的代码，都觉得内心十分澎湃，如果换成现在的我，恐怕再也不会有动力去做这些事情了。

        在学习《计算机图形学》之前，总觉得很多东西高深莫测，但实际掌握了之后，却发现其中了无神秘可言，就如同被原始人像神一样崇拜的火却被现代人叼在嘴上玩弄一样的感觉。图形学的基础之一就是计算几何，但是没有理论数学那么高深莫测，它很有实践性，有时候甚至可以简单到匪夷所思。计算几何是随着计算机和CAD的应用而诞生的一门新兴学科，在国外被称为“计算机辅助几何设计（Computer Aided Geometric Design，CAGD）”。“算法系列”接下来的几篇文章就会介绍一些图形学中常见的计算几何算法（顺便晒晒我的旧代码），都是一些图形学中的基础算法，需要一些图形学的知识和数学知识，但是都不难。不信？那就来看看到底有多难。

        本文是第一篇，主要是一些图形学常用的计算几何方法，涉及到向量、点线关系以及点与多边形关系求解等数学知识，还有一些平面几何的基本原理。事先声明一下，文中涉及的算法实现都是着眼于解释原理以及揭示算法实质的目的，在算法效率和可读性二者的考量上，更注重可读性，有时候为了提高可读性会刻意采取“效率不高”的代码形式，实际工程中使用的代码肯定更紧凑更高效，但是算法原理都是一样的，请读者们对此有正确的认识。

 

一、        判断点是否在矩形内

 

        计算机图形学和数学到底有什么关系？我们先来看几个例子，增加一些感性认识。首先是判断一个点是否在矩形内的算法，这是一个很简单的算法，但是却非常重要。比如你在一个按钮上点击鼠标，系统如何知道你要触发这个按钮对应的事件而不是另一个按钮？对了，就是一个点是否在矩形内的判断处理。Windows 的API提供了PtInRect()函数，实现方法其实就是判断点的x坐标和y坐标是否同时落在矩形的x坐标范围和y坐标范围内，算法实现也很简单：

150 bool IsPointInRect(const Rect& rc,const Point& p)   151 {   152     double xr = (p.x- rc.p1.x)* (p.x- rc.p2.x);   153     double yr = (p.y- rc.p1.y)* (p.y- rc.p2.y);   154    155     return ( (xr<= 0.0)&& (yr <= 0.0) );   156 }

 看看IsPointInRect()函数的实现是否和你想象的不一样？有时候硬件实现乘法有困难或受限制于CPU乘法指令的效率，可以考虑用下面的函数替换，代码繁琐了一点，但是避免了乘法运算：

120 bool IsPointInRect(const Rect& rc,const Point& p)   121 {   122     double xl,xr,yt,yb;   123    124     if(rc.p1.x< rc.p2.x)   125     {   126         xl = rc.p1.x;   127         xr = rc.p2.x;   128     }   129     else   130     {   131         xl = rc.p2.x;   132         xr = rc.p1.x;   133     }   134    135     if(rc.p1.y< rc.p2.y)   136     {   137         yt = rc.p2.y;   138         yb = rc.p1.y;   139     }   140     else   141     {   142         yt = rc.p1.y;   143         yb = rc.p2.y;   144     }   145    146     return ( (p.x>= xl && p.x<= xr) && (p.y >= yb && p.y<= yt) );   147 }

由于IsPointInRect()函数并不假设矩形的两个定点是按照坐标轴升序排列的，所以算法实现时就考虑了所有可能的坐标范围。IsPointInRect()函数使用的是平面直角坐标系，如果不特别说明，本文所有的算法都是基于平面直角坐标系设计的。另外，IsPointInRect()函数没有指定特别的浮点数精度范围，默认是系统浮点数的最大精度，只在某些必须要与0比较的情况下，采用10^-8次方精度，如无特别说明，本文的所有算法都这样处理。

一、        判断点是否在圆内

 

        现在考虑复杂一点，如果图形界面的按钮不是矩形而是圆形的怎么办呢？当然就是判断点是否在圆内部。判断算法的原理就是计算点到圆心的距离d，然后与圆半径r进行比较，若d < r则说明点在圆内，若d = r则说明点在圆上，若d > r则说明点在圆外。这就要提到计算平面上两点距离的算法。以下图为例，计算平面上任意两点之间的距离主要依据著名的勾股定理：

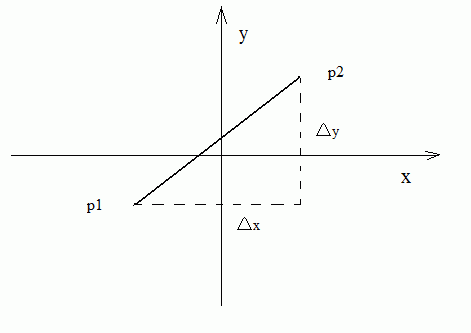
图1 平面两点距离计算示意图

113 //计算欧氏几何空间内平面两点的距离   114 double PointDistance(const Point& p1,const Point& p2)   115 {   116     return std::sqrt((p1.x-p2.x)*(p1.x-p2.x)   117                        + (p1.y-p2.y)*(p1.y-p2.y));   118 }

 

一、        判断点是否在多边形内

 

        现在再考虑复杂一点的，如果按钮是个不规则的多边形区域怎么办？别以为这个考虑没有意义，很多多媒体软件和游戏，通常都是用各种形状的不规则图案作为热点（Hot Spot），Windows也提供了PtInRegion() API，用于判断点是否在一个不规则区域中。我们对问题做一个简化，就判断一个点是否在多边形内？判断点P是否在多边形内是计算几何中一个非常基本的算法，最常用的方法是射线法。以P点为端点，向左方做射线L，然后沿着L从无穷远处开始向P点移动，当遇到多边形的某一条边时，记为与多边形的第一个交点，表示进入多边形内部，继续移动，当遇到另一个交点时，表示离开多边形内部。由此可知，当L与多边形的交点个数是偶数时，表示P点在多边形外，当L与多边形交点个数是奇数时，表示P点在多边形内部。

        由此可见，要实现判断点是否在多边形内的算法，需要知道直线段求交算法，而求交算法又涉及到矢量的一些基本概念，因此在实现这个算法之前，先讲一下矢量的基本概念以及线段求交算法。

 

3.1 矢量的基础知识

         什么是矢量？简单地讲，就是既有大小又有方向的量，数学中又常被称为向量。矢量有几何表示、代数表示和坐标表示等多种表现形式，本文讨论的是几何表示。如果一条线段的端点是有次序之分的，我们把这种线段成为有向线段(Directed Segment)，比如线段P₁P₂，如果起始端点P₁就是坐标原点（0, 0），P₂的坐标是（x, y），则线段P₁P₂的二维矢量坐标表示就是P＝ (x, y)。

 

3.2 矢量的加法和减法

         现在来看几个与矢量有关的重要概念，首先是矢量的加减法。假设有二维矢量P = ( x1, y1 )，Q = ( x2 , y2 )，则矢量加法定义为：

 

P + Q = ( x1 + x2 , y1 + y2 )

 

同样的，矢量减法定义为：

 

P - Q = ( x1 - x2 , y1 - y2 )

 

根据矢量加减法的定义，矢量的加减法满足以下性质：

P + Q = Q + P

P - Q = - ( Q - P )

 

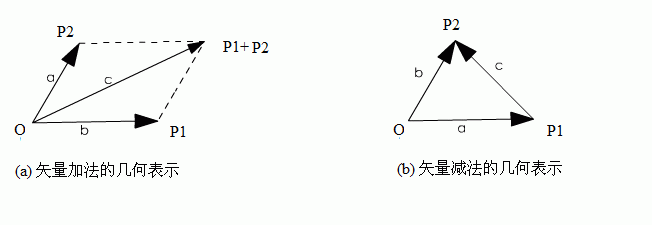
图2 演示了矢量加法和减法的几何意义，由于几何中直线段的两个点不可能刚好在原点，因此线段P₁P₂的矢量其实就是OP₂－ OP₁的结果，如图2 (b)所示：

3.3 矢量的叉积（外积）

         另一个比较重要的概念是矢量的叉积（外积）。计算矢量的叉积是判断直线和线段、线段和线段以及线段和点的位置关系的核心算法。假设有二维矢量P = ( x1, y1 )，Q = ( x2 , y2 )，则矢量的叉积定义为：

 

P × Q = x1*y2 - x2*y1

 

向量叉积的几何意义可以描述为由坐标原点(0,0)、P、Q和P + Q所组成的平行四边形的面积，而且是个带符号的面积，由此可知，矢量的叉积具有以下性质：

 

P × Q = - ( Q × P )

 

叉积的结果P × Q是P和Q所在平面的法矢量，它的方向是垂直与P和Q所在的平面，并且按照P、Q和P × Q的次序构成右手系，所以叉积的另一个非常重要性质是可以通过它的符号可以判断两矢量相互之间位置关系是顺时针还是逆时针关系，具体说明如下：

 

1) 如果 P × Q > 0 , 则Q在P的逆时针方向；

2) 如果 P × Q < 0 , 则Q在P的顺时针方向；

3) 如果 P × Q = 0 , 则Q与P共线（但可能方向是反的）；

 

3.4 矢量的点积（内积）

         最后要介绍的概念是矢量的点积（内积）。假设有二维矢量P = ( x1, y1 )，Q = ( x2 , y2 )，则矢量的点积定义为：

 

P·Q = x1*x2 + y1*y2

 

向量点积的结果是一个标量，它的代数表示是：

 

P·Q = |P| |Q| cos(P, Q)

 

(P, Q) 表示向量P和Q的夹角，如果P和Q不共线，则根据上式可以得到向量点积的一个非常重要的性质，具体说明如下：

 

1) 如果 P · Q > 0 , 则P和Q的夹角是钝角（大于90度）；

2) 如果 P · Q < 0 , 则P和Q的夹角是锐角（小于90度）；

3) 如果 P · Q = 0 , 则P和Q的夹角是90度；

 

        了解了矢量的概念以及矢量的各种运算的几何意义和代数意义后，就可以开始解决各种计算几何的简单问题了，回想本文开始提到的点与多边形的关系问题，首先要解决的就是判断点和直线段的位置关系问题。

 

3.5 用矢量的叉积判断点和直线的关系

 

        根据矢量叉积的几何意义，如果线段所表示的矢量和点的矢量的叉积是0，就说明点在线段所在的直线上，相对于坐标原点O来说，线段的矢量其实就是线段终点P₂=[x2, y2]的矢量OP₂减线段起点P₁=[x1, y1]的矢量OP₁的结果，因此线段P₁P₂的矢量可以表示为P₁P₂＝(x2 – x1, y2 – y1)。如果要判断点P是否在线段P₁P₂上，就要判断矢量P₁P₂和矢量OP的叉积是否是0。需要注意的是，叉积为0只能说明点P与线段P₁P₂所在的直线共线，并不能说明点P一定会落在P₁P₂区间上，因此只是一个必要条件。要正确判断P在线段P₁P₂上，还需要做一个排斥试验，就是检查点P是否在以直线段为对角线的矩形空间内，如果以上两个条件都为真，即可判定点在线段上。有了上述原理，算法实现就比较简单了，以下就是判断点是否在线段上的算法：

174 bool IsPointOnLineSegment(const LineSeg& ls,const Point& pt)   175 {   176     Rect rc;   177    178     GetLineSegmentRect(ls, rc);   179     double cp = CrossProduct(ls.pe.x- ls.ps.x, ls.pe.y- ls.ps.y,   180                              pt.x- ls.ps.x, pt.y- ls.ps.y);//计算叉积   181    182     return ( (IsPointInRect(rc, pt))//排除实验   183              && IsZeroFloatValue(cp)); //1E-8 精度   184 }   185

 

【未完，下篇继续介绍用矢量叉积判断直线和直线段的位置关系，以及判断点与多边形关系的完整算法】