生成学习算法（Generative Learning Algorithms）

　　今天我们来聊一聊生成学习算法，内容主要包括生成模型和判别模型的比较，以及生成学习算法的一个例子——高斯判别分析（Gaussian Discriminant Analysis, GDA）。

1. 生成模型和判别模型

　　前面我们讨论的学习算法（线性回归、逻辑回归、softmax等）都有一个共同点，那就是我们都在想方设法求出$p(y|x;\theta)$，也就是说，给定特征x，我们直接求出y的条件概率作为模型的输出，直接作出判断。这类算法被称为判别学习算法（discriminative learning algorithms）。
　　我们现在考虑另外一种思路，就是从训练集中我们先总结出各个类别的特征分布都是什么样的，也就是得到$p(x|y)$，然后再把要预测的样本特征拿来和每个类别的模型作比较，看它更像是哪种类别的样本。这种算法被称为生成学习算法（generative learning algorithms）。
　　也就是说，判别方法并不关心数据是长什么样子的，它直接面向分类任务，只关心数据之间的区别或者差异，然后利用学习到的区别来对样本作出预测。而生成方法则试图弄清楚数据是怎样产生的，每种类别数据的分布规律是什么，然后对于测试样本，再去判断那个类别最有可能产生这样的数据。
　　那怎么通过各个类别的特征分布判断一个新样本呢？这时就需要用到贝叶斯定理（Bayes rule）了：

$$p(y|x)=\frac{p(x|y)p(y)}{p(x)}$$
我们选出使 $p(y|x)$最大的y作为预测结果。p(x)代表样本在所有类别中出现的总的概率。由于对于某个样本来说，p(x)已经是确定的了，所以我们只需要最大化分子项就可以了：

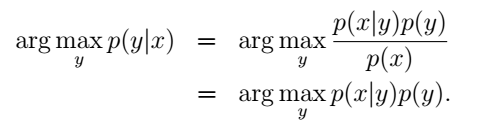
　　这个式子直观上也很好理解：比如我们在马路边远远地望到一个小动物，你想要判断它是一只狗还是一只鹿。首先，你肯定是要观察它的特征，然后根据你之前已经建立的经验，把它分别与狗和鹿的特征相对比，看更像哪个，也就是利用条件概率p(x|y)。然而距离太远了，根据你现在能够观察到的来看，可能和两者的特征都很符合。这个时候如果要让你作出判断的话，我想大多数人都会认为这个在马路边出现的动物是狗。为什么呢？因为狗在城市中更为常见，先验概率p(y=dog)的值更大。在这个过程中，我们便是同时利用了条件概率和先验概率来作出判断的。
　　注意，虽然在这个公式中也出现了 $p(y|x)$，但它和判别模型中要预测的 $p(y|x;\theta)$是不同的。判别模型中我们直接计算出了 $p(y|x;\theta)$的大小，并把它作为预测结果的概率。而在生成模型中，我们是通过选取不同的y，来得到一个最大的 $p(y|x)$，也就是看哪种类别会令测试样本出现的概率最大，把这种类别对应的y值作为预测结果。
　　另外有一个问题，在我看到的资料中都没有明确提到，也可能是我涉猎较少没有发现，但我觉得应该注意的是，训练集中各个类别样本所占比例的问题。我们的生成模型中的p(y)就是由此得到的。有时为了得到充分的样本我们可能会刻意均衡每个类别样本的数量。比如前面马路边小动物分类的问题里，我们在训练集中收集的狗和鹿的数量各占一半。但我们在实际生活中见到它们的比例并不是这样的，可能我们见到狗的概率为……这样我们的p(y)就不是真实的。所以我们的训练集要具有代表性，而不能人为地控制比例。
　　我们首先来讨论一下高斯判别分析模型，感受一下生成方法的概念，并对比了高斯判别分析模型和逻辑回归的联系和区别。后面我们再具体讨论更加经典的生成模型——朴素贝叶斯分类器（Naive Bayes classifier）。

2. 高斯判别分析模型（Gaussian Discriminant Analysis model）

　　作为生成模型的第一个例子，我们来讨论一下高斯判别分析模型（Gaussian Discriminant Analysis model）。这是个什么模型呢？其实很好理解，就是在一个二元分类问题中，类别y依然是服从伯努利分布，然后给定y的情况下，条件概率p(x|y)服从高斯分布，写成数学形式就是这样：

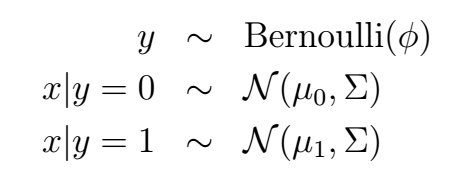
相应的概率分布就是：

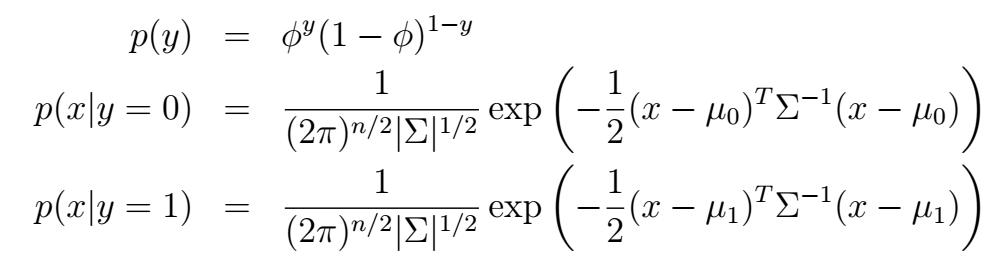
这很好理解吧。它的对数似然函数：

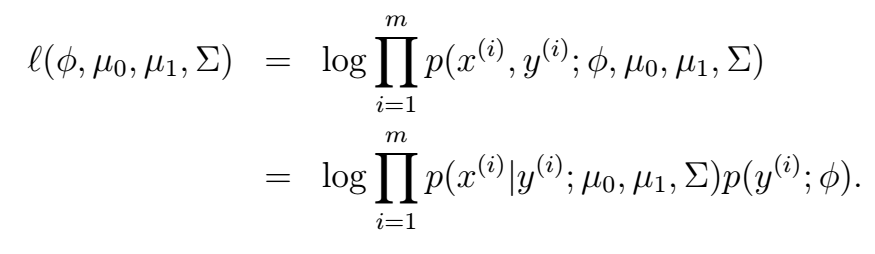
　　好，我们现在从训练数据中学习模型的参数。数学推导的方法与之前我们用到的最大化对数似然函数的方法一致，我们可以得到：
　　
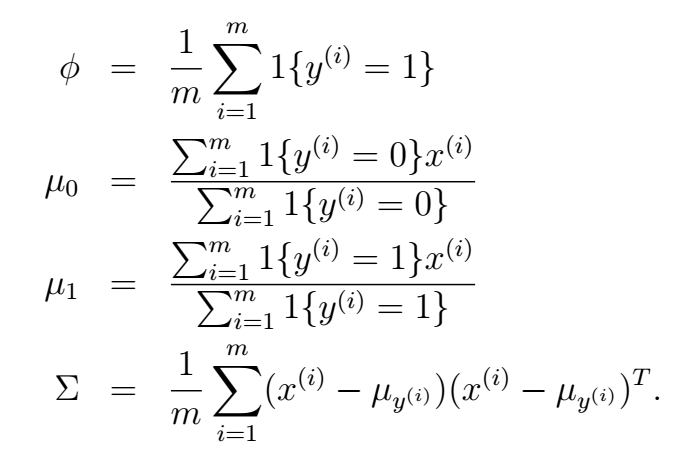
　　再次说明，这里的$1\{\cdot\}$表示逻辑判断，真就输出1 ，反之输出0。这里得到的结果也非常直观，我们可以直观地从这些参数的意义来理解。$\phi$表示的是不同类别在训练集中出现的概率，$\mu_0,\mu_1$分别为不同类别下特征的均值，$\sigma$为训练样本特征的方差。
　　我们把学习到的参数代回到p(x|y=i)中，就可以得到不同类别下样本特征的分布情况了，本例中的分布是这样的：
　　
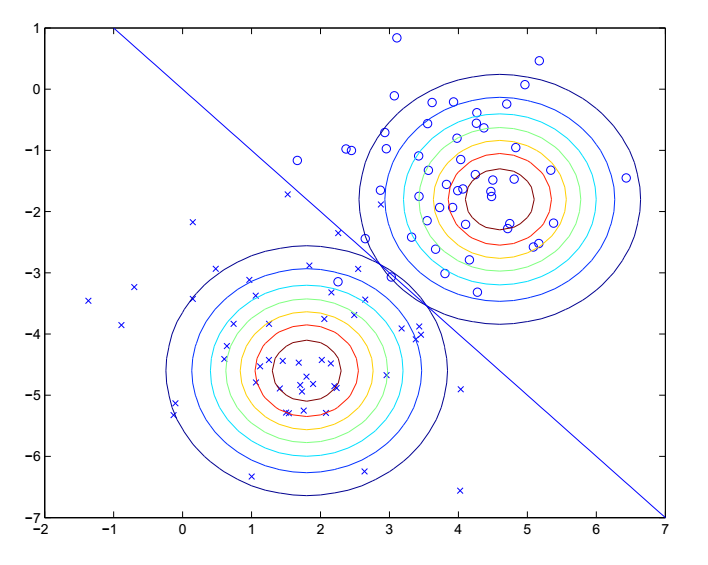
　　这就是两种类别下特征的分布情况，是二维的高斯分布，不同轮廓线代表不同的概率值，越靠近中心的值位置越大。这样，对于每一个测试样本，我们就可以计算出它在不同类别下的条件概率，再结合p(y)，来得出使它出现的概率最大的类别了。

3. 高斯判别分析和逻辑回归的关系

　　从高斯判别分析模型中，如果我们应用贝叶斯定理，计算出y=1关于x的条件概率，我们可以得到：
　　
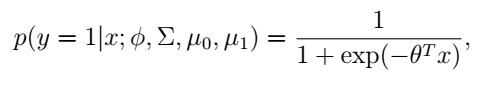
　　为了简洁表示，这里用$\theta$代表模型原来参数的函数。上面这个式子有没有很眼熟？这不就是逻辑回归的形式吗？也就是说我们用一个生成方法推出了一个判别方法的表示！
　　那么这两种方法我们到底应该选择哪种呢？对于同样的训练集，GDA和逻辑回归一般会给出不同的决策边界，那到底哪一种比较好呢？
　　是这样的，从上面的推导过程我们也可以看出，如果$p(x|y)$服从多元高斯分布（而且$\Sigma$相同），那么它的确可以使用逻辑回归来预测；但反过来却不行。也就是说，GDA对数据的假设条件要比逻辑回归强，在一些GDA不适用的情况下，逻辑回归可能仍然使用。但假设条件强的一个优点是，一旦数据满足这些条件，那么GDA将能够更好地拟合数据，给出更好的模型，换句话说，即使是在训练样本很有限的情况下，GDA依然可以给出一个更好的结果。
　　然而，逻辑回归也有它的好处。那就是由于它对数据的假设条件比较弱，因此它更加鲁棒，如果对数据的假设出了点差错，也并不会对它造成多大的影响。它的性格属于“成大事不拘小节”型的。实际上，还有一些其它的数据分布也可以使用逻辑回归，比如泊松分布。相比之下，GDA就只能做专一的“精细活儿”了，如果我们用GDA来预测符合泊松分布的数据，那结果很可能就不怎么好了。
　　总结一下两者的特点就是：GDA模型的假设更强，对于符合要求的数据，可以在更少的样本中学习出有效的结果。逻辑回归则相反，它对数据的假设较弱，但这也使得它对模型假设的偏差问题更加鲁棒。特别地，如果数据不是高斯分布的话，那么在有限的样本集中，逻辑回归通常比GDA表现更好。因此在实际中逻辑回归更加常用。
　　后面我们将要讨论一个更加著名的生成学习算法——朴素贝叶斯分类器（Naive Bayes classifier）。