实验二-多轴水切割运动分析

适用于SEU机器人技术基础-BY SEU_SYZ

实验2：多轴水刀头运动学建模与分析

1实验目的

（1）分析五轴龙门式数控水切割机刀头的运动学；

（2）建立2-DoF水刀头机构的正运动学方程和逆运动学方程；

（3）使用Matlab Robotics Toolbox进行仿真验证；

（4）将水刀头作为末端执行器嫁接到不同机器人末端，实现水切割机器人的动作仿真。

2实验背景

五轴龙门式数控水切割机由龙门架的XYZ三轴和工作部（刀头）的两轴（A轴和C轴）组成。刀头结构中，A轴在YZ平面内与C轴成45°夹角，C轴与参考坐标系的Z轴重合。通过A轴和C轴的旋转，可以获得喷嘴的前倾角δ和偏摆角γ，实现对水射流甩尾和切口斜面的补偿。

3实验内容与结果分析

3.1水刀头2-DOF机器人建模

为了最大程度地仿真水刀头的运动，用D-H参数法建立水刀头的机器人模型时，在a、c处建立真关节，在b、d、e处建立假关节。建立假关节的目的是仿真实际折线形连杆。如此，电机1绕A轴顺时针旋转θ的运动可转化为关节c的关节变量q3,电机2绕C轴逆时针旋转β的运动可以转化为关节a的关节变量q1，且有

编写matlab代码，对2-DOF水刀头建模，将水刀头（即末端执行器）处的坐标系初始化为与参考坐标系同一姿态，并保证初始位姿下C轴与参考坐标系的Z轴重合，A轴在YZ平面内，与C轴成45°夹角。

仿真结果举例：改变q1，q3的值（模拟A、C轴的旋转），如下图所示。

q1=60°,q3=-60°

q1=20°,q3=-20°

3.2水刀头2-DOF机器人正运动学求解

3.2.1问题描述

电机1绕A轴顺时针旋转θ,电机2绕C轴逆时针旋转β，求解前倾角δ、偏摆角γ，其中喷嘴在XZ面的投影与Z轴的夹角即偏摆角γ，在YZ面的投影与Z轴的夹角即前倾角δ。

3.2.2问题分析

由于建模方法的优越性（已将喷嘴即末端执行器的坐标系Fnoa初始化为与参考坐标系Fxyz姿态相同，且喷嘴坐标系中的a轴与Z轴重合），只要求出喷嘴的坐标系a轴在XZ面的投影与Z轴的夹角即偏摆角γ，在YZ面的投影与Z轴的夹角即前倾角δ。

用正运动学函数求出经过关节变量参数组变换后喷嘴的姿态矩阵T，假设T=,提取出喷嘴的a轴方向向量，解算出

,前倾角

3.2.3仿真验证及分析

    如下图所示：输入q1=pi/3,q3=-pi/6,即模拟电机1绕A轴顺时针旋转pi/6,电机2绕C轴逆时针旋转pi/3,得到偏摆角为41.1461°，前倾角为-6.8187°。

    输入q1=pi/4,q3=pi/4,即模拟电机1绕A轴顺时针旋转-pi/4,电机2绕C轴逆时针旋转pi/4,得到偏摆角为81.3007°，前倾角为59.6388°。

3.3水刀头2-DOF机器人逆运动学求解

3.3.1问题描述

    已知前倾角δ、偏摆角γ，求电机1绕A轴顺时针旋转的θ,电机2绕C轴逆时针旋转的β。

3.3.2问题分析

    由方程组

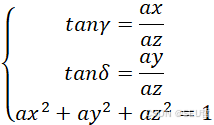
可以解出喷嘴的a轴方向向量

    利用matlab中的symbolic math toolbox自行构造含参数q1,q3的D-H正运动学的方程，得到喷嘴坐标系的姿态矩阵。由于矩阵是由q1,q3表示的，故可以找到三组方程，分别记为

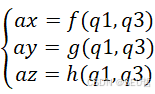
解出此方程，即可得到q1,q3的值，从而得到θ、β。

3.3.3求解过程

    解上述两个方程组，得到

从而

3.3.4仿真验证及分析

    利用正运动学q1=pi/4,q3=pi/4时求出来的前倾角与偏摆角，代入上述公式求出q1,q3。

结果如下图所示；继续改变q1=pi/2,q3=pi/6,经过正运动学求出前倾角和偏摆角后，求解得到如下结果，充分证明了公式的正确性。

4拓展设计

将水刀头作为末端执行器嫁接到实验 1 所选的机器人的末端上，改变关节变量的值即可实现简单动作仿真。结果如图所示。