t-SNE 是一种数据降维技术,通过把高维的数据降到 2~3维,方便使用可视化技术来展示数据。
论文下载
重要参数:
def tsne(X=np.array([]), no_dims=2, initial_dims=50, perplexity=30.0):
- X ∈ R N × D X∈R^{N\times D} X∈RN×D ,N 个样本,每个样本由 D 维数据构成;
- no_dims 压缩后的维度,默认为 2
- init_dims:使用 PCA 对数据预处理,将原始样本集的维度降低至 initial_dims 维度,默认为 30
- perplexity:高斯分布的困惑度,默认为 30;
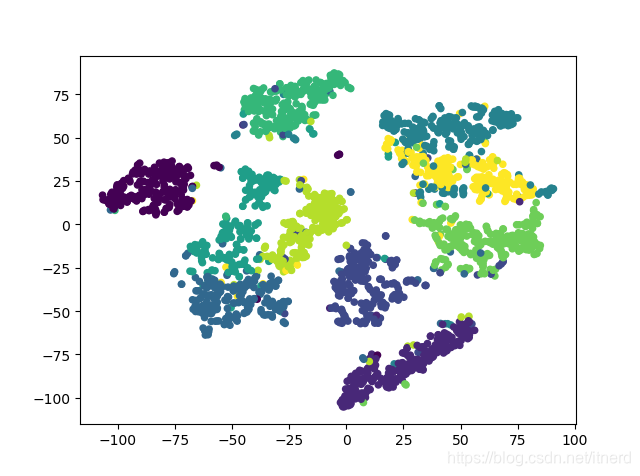
对 MNIST 数据二维可视化
#
# tsne.py
#
# Implementation of t-SNE in Python. The implementation was tested on Python
# 2.7.10, and it requires a working installation of NumPy. The implementation
# comes with an example on the MNIST dataset. In order to plot the
# results of this example, a working installation of matplotlib is required.
#
# The example can be run by executing: `ipython tsne.py`
#
#
# Created by Laurens van der Maaten on 20-12-08.
# Copyright (c) 2008 Tilburg University. All rights reserved.
import numpy as np
import pylab
def Hbeta(D=np.array([]), beta=1.0):
"""
Compute the perplexity and the P-row for a specific value of the
precision of a Gaussian distribution.
"""
# Compute P-row and corresponding perplexity
P = np.exp(-D.copy() * beta)
sumP = sum(P)
H = np.log(sumP) + beta * np.sum(D * P) / sumP
P = P / sumP
return H, P
def x2p(X=np.array([]), tol=1e-5, perplexity=30.0):
"""
Performs a binary search to get P-values in such a way that each
conditional Gaussian has the same perplexity.
"""
# Initialize some variables
print("Computing pairwise distances...")
(n, d) = X.shape
sum_X = np.sum(np.square(X), 1)
D = np.add(np.add(-2 * np.dot(X, X.T), sum_X).T, sum_X)
P = np.zeros((n, n))
beta = np.ones((n, 1))
logU = np.log(perplexity)
# Loop over all datapoints
for i in range(n):
# Print progress
if i % 500 == 0:
print("Computing P-values for point %d of %d..." % (i, n))
# Compute the Gaussian kernel and entropy for the current precision
betamin = -np.inf
betamax = np.inf
Di = D[i, np.concatenate((np.r_[0:i], np.r_[i+1:n]))]
(H, thisP) = Hbeta(Di, beta[i])
# Evaluate whether the perplexity is within tolerance
Hdiff = H - logU
tries = 0
while np.abs(Hdiff) > tol and tries < 50:
# If not, increase or decrease precision
if Hdiff > 0:
betamin = beta[i].copy()
if betamax == np.inf or betamax == -np.inf:
beta[i] = beta[i] * 2.
else:
beta[i] = (beta[i] + betamax) / 2.
else:
betamax = beta[i].copy()
if betamin == np.inf or betamin == -np.inf:
beta[i] = beta[i] / 2.
else:
beta[i] = (beta[i] + betamin) / 2.
# Recompute the values
(H, thisP) = Hbeta(Di, beta[i])
Hdiff = H - logU
tries += 1
# Set the final row of P
P[i, np.concatenate((np.r_[0:i], np.r_[i+1:n]))] = thisP
# Return final P-matrix
print("Mean value of sigma: %f" % np.mean(np.sqrt(1 / beta)))
return P
def pca(X=np.array([]), no_dims=50):
"""
Runs PCA on the NxD array X in order to reduce its dimensionality to
no_dims dimensions.
"""
print("Preprocessing the data using PCA...")
(n, d) = X.shape
X = X - np.tile(np.mean(X, 0), (n, 1))
(l, M) = np.linalg.eig(np.dot(X.T, X))
Y = np.dot(X, M[:, 0:no_dims])
return Y
def tsne(X=np.array([]), no_dims=2, initial_dims=50, perplexity=30.0):
"""
Runs t-SNE on the dataset in the NxD array X to reduce its
dimensionality to no_dims dimensions. The syntaxis of the function is
`Y = tsne.tsne(X, no_dims, perplexity), where X is an NxD NumPy array.
"""
# Check inputs
if isinstance(no_dims, float):
print("Error: array X should have type float.")
return -1
if round(no_dims) != no_dims:
print("Error: number of dimensions should be an integer.")
return -1
# Initialize variables
X = pca(X, initial_dims).real
(n, d) = X.shape
max_iter = 1000
initial_momentum = 0.5
final_momentum = 0.8
eta = 500
min_gain = 0.01
Y = np.random.randn(n, no_dims)
dY = np.zeros((n, no_dims))
iY = np.zeros((n, no_dims))
gains = np.ones((n, no_dims))
# Compute P-values
P = x2p(X, 1e-5, perplexity)
P = P + np.transpose(P)
P = P / np.sum(P)
P = P * 4. # early exaggeration
P = np.maximum(P, 1e-12)
# Run iterations
for iter in range(max_iter):
# Compute pairwise affinities
sum_Y = np.sum(np.square(Y), 1)
num = -2. * np.dot(Y, Y.T)
num = 1. / (1. + np.add(np.add(num, sum_Y).T, sum_Y))
num[range(n), range(n)] = 0.
Q = num / np.sum(num)
Q = np.maximum(Q, 1e-12)
# Compute gradient
PQ = P - Q
for i in range(n):
dY[i, :] = np.sum(np.tile(PQ[:, i] * num[:, i], (no_dims, 1)).T * (Y[i, :] - Y), 0)
# Perform the update
if iter < 20:
momentum = initial_momentum
else:
momentum = final_momentum
gains = (gains + 0.2) * ((dY > 0.) != (iY > 0.)) + \
(gains * 0.8) * ((dY > 0.) == (iY > 0.))
gains[gains < min_gain] = min_gain
iY = momentum * iY - eta * (gains * dY)
Y = Y + iY
Y = Y - np.tile(np.mean(Y, 0), (n, 1))
# Compute current value of cost function
if (iter + 1) % 10 == 0:
C = np.sum(P * np.log(P / Q))
print("Iteration %d: error is %f" % (iter + 1, C))
# Stop lying about P-values
if iter == 100:
P = P / 4.
# Return solution
return Y
if __name__ == "__main__":
print("Run Y = tsne.tsne(X, no_dims, perplexity) to perform t-SNE on your dataset.")
print("Running example on 2,500 MNIST digits...")
X = np.loadtxt("mnist2500_X.txt")
labels = np.loadtxt("mnist2500_labels.txt")
Y = tsne(X, 2, 50, 20.0)
pylab.scatter(Y[:, 0], Y[:, 1], 20, labels)
pylab.show()








 本文介绍了一种名为t-SNE的数据降维技术,该技术能够将高维数据降至2到3维,便于进行数据可视化。文章详细描述了t-SNE的实现过程,包括关键参数的设置和对MNIST数据集的可视化应用。
本文介绍了一种名为t-SNE的数据降维技术,该技术能够将高维数据降至2到3维,便于进行数据可视化。文章详细描述了t-SNE的实现过程,包括关键参数的设置和对MNIST数据集的可视化应用。

















 623
623

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










