TensorFlow2.0 Guide 官方教程学习笔记13- Ragged Tensors

最新推荐文章于 2024-09-07 09:34:19 发布

黄水生

最新推荐文章于 2024-09-07 09:34:19 发布

阅读量4k

点赞数 3

分类专栏： TensorFlow 2.0 学习笔记文章标签： TensorFlow2.0

本文链接：https://blog.csdn.net/jackhh1/article/details/102690290

版权

TensorFlow 2.0 学习笔记专栏收录该内容

24 篇文章

订阅专栏

本笔记参照TensorFlow官方教程，主要是对‘Ragged Tensors’教程内容翻译和内容结构编排，原文链接：Ragged Tensors

创建环境（Setup）

from __future__ import absolute_import, division, print_function, unicode_literals

import math
try:
  %tensorflow_version 2.x
except Exception:
  pass
import tensorflow as tf

一、概览

因为我们的数据有不同形状，所以我们的张量也会有不同的形状。不规则张量等价于TensorFlow中嵌套的变长列表。他们使得存储和处理非均匀形状的数据变得容易。包括：

可变长度特征，比如一个电影的演员名单。
批的可变长度顺序输入，如句子或视频剪辑。
层次输入，例如文本文档，它被细分为节、段落、句子和单词。
结构化输入中的单个字段，如协议缓冲区。

1.1 我们能用不规则张量做什么

超过一百多张TensorFlow操作支持不规则张量，包括数学运算（比如tf.add、tf.reduce_mean），数组运算（比如tf.concat、tf.tile），字符控制循环（tf.substr）和许多其它：

digits = tf.ragged.constant([[3, 1, 4, 1], [], [5, 9, 2], [6], []])
words = tf.ragged.constant([["So", "long"], ["thanks", "for", "all", "the", "fish"]])
print(tf.add(digits, 3))
print(tf.reduce_mean(digits, axis=1))
print(tf.concat([digits, [[5, 3]]], axis=0))
print(tf.tile(digits, [1, 2]))
print(tf.strings.substr(words, 0, 2))

<tf.RaggedTensor [[6, 4, 7, 4], [], [8, 12, 5], [9], []]>
tf.Tensor([2.25              nan 5.33333333 6.                nan], shape=(5,), dtype=float64)
<tf.RaggedTensor [[3, 1, 4, 1], [], [5, 9, 2], [6], [], [5, 3]]>
<tf.RaggedTensor [[3, 1, 4, 1, 3, 1, 4, 1], [], [5, 9, 2, 5, 9, 2], [6, 6], []]>
<tf.RaggedTensor [[b'So', b'lo'], [b'th', b'fo', b'al', b'th', b'fi']]>

还有为不规则张量特定的方法和操作，包括工厂方法、转换方法和值映射操作。相关支持ops列表，请参考tf.ragged文档（链接未知）

与普通张量一样，您可以使用python风格的索引来访问不规则张量的特定切片。有关更多信息，请参见下面的索引一节。

print(digits[0])       # First row

tf.Tensor([3 1 4 1], shape=(4,), dtype=int32)

print(digits[:, :2])   # First two values in each row.

<tf.RaggedTensor [[3, 1], [], [5, 9], [6], []]>

print(digits[:, -2:])  # Last two values in each row.

<tf.RaggedTensor [[4, 1], [], [9, 2], [6], []]>

和普通的张量一样，我们可以使用Python算术和比较运算符来执行elementwise操作。更多信息，请参见下面的过载操作符一节。

print(digits + 3)

<tf.RaggedTensor [[6, 4, 7, 4], [], [8, 12, 5], [9], []]>

print(digits + tf.ragged.constant([[1, 2, 3, 4], [], [5, 6, 7], [8], []]))

<tf.RaggedTensor [[4, 3, 7, 5], [], [10, 15, 9], [14], []]>

如果需要对不规则张量的值进行元素转换（elementwise transformation），可以使用tf.ragged.map_flat_values,它接受一个函数加上一个或多个参数，并应有这个函数转换不规则张量的值。

times_two_plus_one = lambda x: x * 2 + 1
print(tf.ragged.map_flat_values(times_two_plus_one, digits))

<tf.RaggedTensor [[7, 3, 9, 3], [], [11, 19, 5], [13], []]>

1.2 创建一个不规则张量

构造不规则张量最简单的方法是使用tf.ragged.constant，它构建了与给定的嵌套Python列表相对应的不规则张量。

sentences = tf.ragged.constant([
    ["Let's", "build", "some", "ragged", "tensors", "!"],
    ["We", "can", "use", "tf.ragged.constant", "."]])
print(sentences)

<tf.RaggedTensor [[b"Let's", b'build', b'some', b'ragged', b'tensors', b'!'], [b'We', b'can', b'use', b'tf.ragged.constant', b'.']]>

paragraphs = tf.ragged.constant([
    [['I', 'have', 'a', 'cat'], ['His', 'name', 'is', 'Mat']],
    [['Do', 'you', 'want', 'to', 'come', 'visit'], ["I'm", 'free', 'tomorrow']],
])
print(paragraphs)

<tf.RaggedTensor [[[b'I', b'have', b'a', b'cat'], [b'His', b'name', b'is', b'Mat']], [[b'Do', b'you', b'want', b'to', b'come', b'visit'], [b"I'm", b'free', b'tomorrow']]]>

还可以通过将平面张量与行分区张量配对来构造不规则张量，这表明应该使用工厂类方法。比如:tf.RaggedTensor.from_value_rowids,tf.RaggedTensor.from_row_lengths,and tf.RaggedTensor.from_row_splits.

tf.RaggedTensor.from_value_rowids
如果我们知道每个值属于哪一行，那么我们可以用一个行标识值（value-rowids）行分隔张量（row-partitioning）来构建一个不规则张量：

print(tf.RaggedTensor.from_value_rowids(
    values=[3, 1, 4, 1, 5, 9, 2, 6],
    value_rowids=[0, 0, 0, 0, 2, 2, 2, 3]))

<tf.RaggedTensor [[3, 1, 4, 1], [], [5, 9, 2], [6]]>

tf.RaggedTensor.from_row_lengths
如果我们知道每一行的长度，那我们可以用‘row_lengths’将张量进行行分隔：

print(tf.RaggedTensor.from_row_lengths(
    values=[3, 1, 4, 1, 5, 9, 2, 6],
    row_lengths=[4, 0, 3, 1]))

<tf.RaggedTensor [[3, 1, 4, 1], [], [5, 9, 2], [6]]>

tf.RaggedTensor.from_row_splits
如果我们知道每行开始和结束的索引，那么我们可以使用一个’row_splits’将张量按行分隔：

print(tf.RaggedTensor.from_row_splits(
    values=[3, 1, 4, 1, 5, 9, 2, 6],
    row_splits=[0, 4, 4, 7, 8]))

<tf.RaggedTensor [[3, 1, 4, 1], [], [5, 9, 2], [6]]>

详情可以参考‘tf.RaggedTensor’文档（未看到链接）

1.3 我们能在不规则张量里存储什么

与常规张量一样，不规则张量中的值必须具有相同的类型；所有的值必须在相同的嵌套深度（张量的秩）：

print(tf.ragged.constant([["Hi"], ["How", "are", "you"]]))  # ok: type=string, rank=2

<tf.RaggedTensor [[b'Hi'], [b'How', b'are', b'you']]>

print(tf.ragged.constant([[[1, 2], [3]], [[4, 5]]]))        # ok: type=int32, rank=3

<tf.RaggedTensor [[[1, 2], [3]], [[4, 5]]]>

try:
  tf.ragged.constant([["one", "two"], [3, 4]])              # bad: multiple types
except ValueError as exception:
  print(exception)

Can't convert Python sequence with mixed types to Tensor.

try:
  tf.ragged.constant(["A", ["B", "C"]])                     # bad: multiple nesting depths
except ValueError as exception:
  print(exception)

all scalar values must have the same nesting depth

1.4 用例

下面的示例演示了如何使用不规则张量为一个可变长度查询批构造和组合单字符和双字符嵌入，并为每个句子的开头和结尾使用特殊标记。有关本例中使用的ops的更多细节，请参见tf.ragged方案文档：

queries = tf.ragged.constant([['Who', 'is', 'Dan', 'Smith'],
                              ['Pause'],
                              ['Will', 'it', 'rain', 'later', 'today']])

# Create an embedding table.
num_buckets = 1024
embedding_size = 4
embedding_table = tf.Variable(
    tf.random.truncated_normal([num_buckets, embedding_size],
                       stddev=1.0 / math.sqrt(embedding_size)))

# Look up the embedding for each word.
word_buckets = tf.strings.to_hash_bucket_fast(queries, num_buckets)
word_embeddings = tf.ragged.map_flat_values(
    tf.nn.embedding_lookup, embedding_table, word_buckets)                  # ①

# Add markers to the beginning and end of each sentence.
marker = tf.fill([queries.nrows(), 1], '#')
padded = tf.concat([marker, queries, marker], axis=1)                       # ②

# Build word bigrams & look up embeddings.
bigrams = tf.strings.join([padded[:, :-1],
                               padded[:, 1:]],
                              separator='+')                                # ③

bigram_buckets = tf.strings.to_hash_bucket_fast(bigrams, num_buckets)
bigram_embeddings = tf.ragged.map_flat_values(
    tf.nn.embedding_lookup, embedding_table, bigram_buckets)                # ④

# Find the average embedding for each sentence
all_embeddings = tf.concat([word_embeddings, bigram_embeddings], axis=1)    # ⑤
avg_embedding = tf.reduce_mean(all_embeddings, axis=1)                      # ⑥
print(avg_embedding)

tf.Tensor(
[[ 0.13143723 -0.00718623 -0.10956167 -0.09767713]
 [-0.04679693  0.08434612 -0.1436042  -0.10770806]
 [ 0.04992997  0.3014398   0.11872023  0.27833948]], shape=(3, 4), dtype=float32)

在这里插入图片描述

二、不规则张量：定义

2.1 不规则和统一维度

不规则张量是一个具有一个或多个不规则维的张量，这些维的切片可能有不同的长度。例如，rt=[[3, 1, 4, 1], [], [5, 9, 2], [6], []] 的内部（列）维是不规则的，因为列切片（rt[0, :], …, rt[4, :]）有不同的长度。其切片长度相同的维度称为均匀维度。
不规则张量的最外层维度总是一致的，因为它包含一个切片（所以不可能有不同的切片长度）。除了均匀的外层维度外，不规则张量也可能具有统一的内部维度。例如，我们可以使用形状为‘[num_sentences, (num_words), embedding_size]’不规则张量将每个单词嵌入存储在一批句子中，其中(num_words)周围的括号表示维度是不规则的。
在这里插入图片描述
不规则张量可能有多重不规则维。例如，我们可以用一个形状为[num_documents, (num_paragraphs), (num_sentences), (num_words)] 的张量用来存储一批（batch）文本文档的结构。（括号表示不规则维）

不规则张量形状的限制

	不规则张量的形状目前被限制为如下形式：
		- 一个单一均匀维度（uniform dimension）
		- 随后是一个或多个不规则维度（uniform dimension）
	 	- 随后是0个或多个均匀维度（uniform dimension）
	 这些限制是当前实现的结果，将来谷歌可能会放宽

2.2 秩和不规则秩

不规则张量维度的总数是它的秩，而不规则维度数是它的不规则秩。在图执行模式（非即刻执行模式），一个张量的不规则秩在创建时就被固定了：它不会随着运行值改变，也不能为不同的运行回话动态的改变。一个潜在的不规则张量是指它的值可能是‘tf.Tensor’，也可能是‘tf.RaggedTensor’。'tf.Tensor’的不规则秩是0。

2.3 不规则秩的形状

当描述不规则张量的形状，不规则维会以括号的形式显示。例如，上面讲到的例子中，一个嵌套存储一个批句子(a batch of sentences)的每个单词的3-D不规则张量的形状可以这样写：‘[num_sentences, (num_words), embedding_size]’。当不规则张量的维为‘None’时，RaggedTensor.shape的属性返回的是tf.TensorShape。

tf.ragged.constant([["Hi"], ["How", "are", "you"]]).shape

TensorShape([2, None])

tf.RaggedTensor.bounding_shape可以用来为一个给定的不规则张量找到一个紧密的边界形状（tight bounding shape）：

print(tf.ragged.constant([["Hi"], ["How", "are", "you"]]).bounding_shape())

tf.Tensor([2 3], shape=(2,), dtype=int64)

三、不规则张量和稀疏张量（sparse tensors）的对比

一个不规则张量不应该被认为是一个稀疏张量的类型，而应该是一个形状不规则的稠密张量（dense tensor）。
作为一个说明性的例子，考虑如何为不规则张量和稀疏张量定义注入concat、stack和tile之类的数组操作。按行连接不规则张量，形成一个组合长度的单行：
在这里插入图片描述

ragged_x = tf.ragged.constant([["John"], ["a", "big", "dog"], ["my", "cat"]])
ragged_y = tf.ragged.constant([["fell", "asleep"], ["barked"], ["is", "fuzzy"]])
print(tf.concat([ragged_x, ragged_y], axis=1))

<tf.RaggedTensor [[b'John', b'fell', b'asleep'], [b'a', b'big', b'dog', b'barked'], [b'my', b'cat', b'is', b'fuzzy']]>

但连接稀疏张量相当于连接相应的稠密张量（dense tensors），如下面的例子所示（Ø表明缺失值）：
在这里插入图片描述

sparse_x = ragged_x.to_sparse()
sparse_y = ragged_y.to_sparse()
sparse_result = tf.sparse.concat(sp_inputs=[sparse_x, sparse_y], axis=1)
print(tf.sparse.to_dense(sparse_result, ''))

tf.Tensor(
[[b'John' b'' b'' b'fell' b'asleep']
 [b'a' b'big' b'dog' b'barked' b'']
 [b'my' b'cat' b'' b'is' b'fuzzy']], shape=(3, 5), dtype=string)

关于为什么这种区别如此重要的另一个例子，考虑下‘每行平均值’的操作（op）比如：‘tf.reduce_mealn’。对于一个不规则张量，一行的平均值是行值除以行的宽度的和。但是对于一个稀疏张量来说，一个行的平均值是这个行的值除以稀疏张量的总宽度（它大于或等于最长行的宽度）的和。

四、重载操作

不规则张量重载了标准的Python算术和比较运算符，使得执行基本的元素数学变得容易：

x = tf.ragged.constant([[1, 2], [3], [4, 5, 6]])
y = tf.ragged.constant([[1, 1], [2], [3, 3, 3]])
print(x + y)

<tf.RaggedTensor [[2, 3], [5], [7, 8, 9]]>

由于重载操作符执行元素计算，所以所有二级制操作的输入必须具有相同的形状，或者可以广播为相同的形状。在最简单的广播情况下，单个标量是元素与不规则张量中的每个值的组合：

x = tf.ragged.constant([[1, 2], [3], [4, 5, 6]])
print(x + 3)

<tf.RaggedTensor [[4, 5], [6], [7, 8, 9]]>

更多高级的用例，可以参考‘Broadcasting’。（未给出链接）

不规则张量重载与普通张量相同的一组运算符:一元运算符-、~和abs();和二进制运算符+、-、、/、/ / %, *,&,|,^,= =、<、< =、>、> =。

五、索引

不规则张量支持Python风格索引，包括多维索引和切片。下面的例子用2-D和3-D不规则张量演示不规则张量索引。

5.1 用1级不规则度索引一个2-D不规则张量

queries = tf.ragged.constant(
    [['Who', 'is', 'George', 'Washington'],
     ['What', 'is', 'the', 'weather', 'tomorrow'],
     ['Goodnight']])
print(queries[1])

tf.Tensor([b'What' b'is' b'the' b'weather' b'tomorrow'], shape=(5,), dtype=string)

print(queries[1, 2])                # A single word

tf.Tensor(b'the', shape=(), dtype=string)

print(queries[1:])                  # Everything but the first row

<tf.RaggedTensor [[b'What', b'is', b'the', b'weather', b'tomorrow'], [b'Goodnight']]>

print(queries[:, :3])               # The first 3 words of each query

<tf.RaggedTensor [[b'Who', b'is', b'George'], [b'What', b'is', b'the'], [b'Goodnight']]>

print(queries[:, -2:])              # The last 2 words of each query

<tf.RaggedTensor [[b'George', b'Washington'], [b'weather', b'tomorrow'], [b'Goodnight']]>

5.2 用2级不规则度索引一个3-D不规则张量

rt = tf.ragged.constant([[[1, 2, 3], [4]],
                         [[5], [], [6]],
                         [[7]],
                         [[8, 9], [10]]])

print(rt[1])                        # Second row (2-D RaggedTensor)

<tf.RaggedTensor [[5], [], [6]]>

print(rt[3, 0])                     # First element of fourth row (1-D Tensor)

tf.Tensor([8 9], shape=(2,), dtype=int32)

print(rt[:, 1:3])                   # Items 1-3 of each row (3-D RaggedTensor)

<tf.RaggedTensor [[[4]], [[], [6]], [], [[10]]]>

print(rt[:, -1:])                   # Last item of each row (3-D RaggedTensor)

<tf.RaggedTensor [[[4]], [[6]], [[7]], [[10]]]>

不规则张量支持多维索引和切片，但有一个限制：不允许对一个不规则维进行索引。这种情况是用问题的，因为索引值可能存在于某些行中，而不存在于其他行中。在这种情况下，我们不知道是否应该(1)提出一个IndexError;(2)使用默认值;或者(3)跳过那个值，返回一个行数比开始时少的张量。根据Python的指导原则(“面对歧义，拒绝猜测的诱惑”)，TensorFlow目前不允许这种操作。

六、张量类型转换

不规则张量类定义了可用于不规则张量与‘tf.Tensor’或‘tf.SparseTensors’之间转换的方法：

ragged_sentences = tf.ragged.constant([
    ['Hi'], ['Welcome', 'to', 'the', 'fair'], ['Have', 'fun']])
print(ragged_sentences.to_tensor(default_value=''))

tf.Tensor(
[[b'Hi' b'' b'' b'']
 [b'Welcome' b'to' b'the' b'fair']
 [b'Have' b'fun' b'' b'']], shape=(3, 4), dtype=string)

print(ragged_sentences.to_sparse())

SparseTensor(indices=tf.Tensor(
[[0 0]
 [1 0]
 [1 1]
 [1 2]
 [1 3]
 [2 0]
 [2 1]], shape=(7, 2), dtype=int64), values=tf.Tensor([b'Hi' b'Welcome' b'to' b'the' b'fair' b'Have' b'fun'], shape=(7,), dtype=string), dense_shape=tf.Tensor([3 4], shape=(2,), dtype=int64))

x = [[1, 3, -1, -1], [2, -1, -1, -1], [4, 5, 8, 9]]
print(tf.RaggedTensor.from_tensor(x, padding=-1))

<tf.RaggedTensor [[1, 3], [2], [4, 5, 8, 9]]>

st = tf.SparseTensor(indices=[[0, 0], [2, 0], [2, 1]],
                     values=['a', 'b', 'c'],
                     dense_shape=[3, 3])
print(tf.RaggedTensor.from_sparse(st))

<tf.RaggedTensor [[b'a'], [], [b'b', b'c']]>

七、评价不规则张量

7.1 即刻执行

在即可执行模式，不规则张量可以被立即评价。为了获取不规则张量里的值，我们可以：

使用‘tf.RaggedTensor.to_list()’方法，它可以将不规则张量转换为Python序列。

rt = tf.ragged.constant([[1, 2], [3, 4, 5], [6], [], [7]])
print(rt.to_list())

[[1, 2], [3, 4, 5], [6], [], [7]]

使用Python索引。如果我们选择的张量片没有不规则维，那它将返回一个即刻张量（EagerTensor）。我们可以使用numpy()方法直接获取这些值

print(rt[1].numpy())

[3 4 5]

将不规则张量分解成它的分量，可以用tf.RaggedTensor.values和tf.RaggedTensor.row_splits属性，也可以用行分割方法，比如：tf.RaggedTensor.row_lengths()和tf.RaggedTensor.value_rowids()。

print(rt.values)

tf.Tensor([1 2 3 4 5 6 7], shape=(7,), dtype=int32)

print(rt.row_splits)

tf.Tensor([0 2 5 6 6 7], shape=(6,), dtype=int64)

7.2 广播

广播是使不同形状（shape）的张量在进行元素运算时具有兼容性形状的过程。有关广播的更多背景资料，请参阅：

Numpy Broadcasting
tf.broadcast_dynamic_shape
tf.broadcast_to
广播两个输入X和Y，让它们有兼容形状的基本步骤是：
1.如果X和Y没有相同数目的维，可以添加外层维（1维），知道它们具有相同的维数
2.对于X和Y有不同的维：
- 如果X或Y在维度d中大小为1（If x or y have size 1 in dimension d），则跨维度d重复其值以匹配其它输入的大小。
- 否则，引发异常（x和y之间广播不兼容）
其中，一个张量在一个均匀维中的大小是一个数字（该维上的切片的大小）;一个不规则维中的张量大小是一个切片长度的列表（对于该维度上的所有切片）

广播示例

# x       (2D ragged):  2 x (num_rows)
# y       (scalar)
# result  (2D ragged):  2 x (num_rows)
x = tf.ragged.constant([[1, 2], [3]])
y = 3
print(x + y)

<tf.RaggedTensor [[4, 5], [6]]>

# x         (2d ragged):  3 x (num_rows)
# y         (2d tensor):  3 x          1
# Result    (2d ragged):  3 x (num_rows)
x = tf.ragged.constant(
   [[10, 87, 12],
    [19, 53],
    [12, 32]])
y = [[1000], [2000], [3000]]
print(x + y)

<tf.RaggedTensor [[1010, 1087, 1012], [2019, 2053], [3012, 3032]]>

# x      (3d ragged):  2 x (r1) x 2
# y      (2d ragged):         1 x 1
# Result (3d ragged):  2 x (r1) x 2
x = tf.ragged.constant(
    [[[1, 2], [3, 4], [5, 6]],
     [[7, 8]]],
    ragged_rank=1)
y = tf.constant([[10]])
print(x + y)

<tf.RaggedTensor [[[11, 12], [13, 14], [15, 16]], [[17, 18]]]>

# x      (3d ragged):  2 x (r1) x (r2) x 1
# y      (1d tensor):                    3
# Result (3d ragged):  2 x (r1) x (r2) x 3
x = tf.ragged.constant(
    [
        [
            [[1], [2]],
            [],
            [[3]],
            [[4]],
        ],
        [
            [[5], [6]],
            [[7]]
        ]
    ],
    ragged_rank=2)
y = tf.constant([10, 20, 30])
print(x + y)

<tf.RaggedTensor [[[[11, 21, 31], [12, 22, 32]], [], [[13, 23, 33]], [[14, 24, 34]]], [[[15, 25, 35], [16, 26, 36]], [[17, 27, 37]]]]>

下面是一些不能广播的示例：

# x      (2d ragged): 3 x (r1)
# y      (2d tensor): 3 x    4  # trailing dimensions do not match
x = tf.ragged.constant([[1, 2], [3, 4, 5, 6], [7]])
y = tf.constant([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
try:
  x + y
except tf.errors.InvalidArgumentError as exception:
  print(exception)

Expected 'tf.Tensor(False, shape=(), dtype=bool)' to be true. Summarized data: b'Unable to broadcast: dimension size mismatch in dimension'
1
b'lengths='
4
b'dim_size='
2, 4, 1

# x      (2d ragged): 3 x (r1)
# y      (2d ragged): 3 x (r2)  # ragged dimensions do not match.
x = tf.ragged.constant([[1, 2, 3], [4], [5, 6]])
y = tf.ragged.constant([[10, 20], [30, 40], [50]])
try:
  x + y
except tf.errors.InvalidArgumentError as exception:
  print(exception)

Expected 'tf.Tensor(False, shape=(), dtype=bool)' to be true. Summarized data: b'Unable to broadcast: dimension size mismatch in dimension'
1
b'lengths='
2, 2, 1
b'dim_size='
3, 1, 2

# x      (3d ragged): 3 x (r1) x 2
# y      (3d ragged): 3 x (r1) x 3  # trailing dimensions do not match
x = tf.ragged.constant([[[1, 2], [3, 4], [5, 6]],
                        [[7, 8], [9, 10]]])
y = tf.ragged.constant([[[1, 2, 0], [3, 4, 0], [5, 6, 0]],
                        [[7, 8, 0], [9, 10, 0]]])
try:
  x + y
except tf.errors.InvalidArgumentError as exception:
  print(exception)

Expected 'tf.Tensor(False, shape=(), dtype=bool)' to be true. Summarized data: b'Unable to broadcast: dimension size mismatch in dimension'
2
b'lengths='
3, 3, 3, 3, 3
b'dim_size='
2, 2, 2, 2, 2

八、不规则张量编码

不规则张量使用‘RaggedTensor’类来编码。在内部，每个不规则张量包含：
- 一个张量值，它把可变长度的行连接成一个扁平的列表
- 一个‘row_splits’（行分隔）向量，表示这些扁平的列表如何按行分割。尤其注意，行的值‘rt[i]’存储在切片rt.values[rt.row_splits[i]:rt.row_splits[i+1]]
在这里插入图片描述

rt = tf.RaggedTensor.from_row_splits(
    values=[3, 1, 4, 1, 5, 9, 2],
    row_splits=[0, 4, 4, 6, 7])
print(rt)

<tf.RaggedTensor [[3, 1, 4, 1], [], [5, 9], [2]]>

8.1 多不规则度

一个具有多个不规则维的不规则张量通过对张量值使用嵌套的不规则张量进行编码。每个嵌套的不规则张量都增加了一个单独的不规则维。
在这里插入图片描述

rt = tf.RaggedTensor.from_row_splits(
    values=tf.RaggedTensor.from_row_splits(
        values=[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
        row_splits=[0, 3, 3, 5, 9, 10]),
    row_splits=[0, 1, 1, 5])
print(rt)
print("Shape: {}".format(rt.shape))
print("Number of ragged dimensions: {}".format(rt.ragged_rank))

<tf.RaggedTensor [[[10, 11, 12]], [], [[], [13, 14], [15, 16, 17, 18], [19]]]>
Shape: (3, None, None)
Number of ragged dimensions: 2

工厂函数：tf.RaggedTensor.from_nested_row_splits可用于直接构造一个具有多不规则维的不规则整理，方法是提供一个‘row_splits’张量列表：

rt = tf.RaggedTensor.from_nested_row_splits(
    flat_values=[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
    nested_row_splits=([0, 1, 1, 5], [0, 3, 3, 5, 9, 10]))
print(rt)

<tf.RaggedTensor [[[10, 11, 12]], [], [[], [13, 14], [15, 16, 17, 18], [19]]]>

8.2 均匀内部维度（Uniform Inner Dimensions）

带有均匀内部为的不规则张量采用多维tf.Tensor进行编码
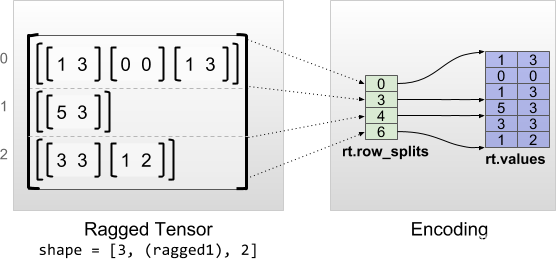
在这里插入图片描述

rt = tf.RaggedTensor.from_row_splits(
    values=[[1, 3], [0, 0], [1, 3], [5, 3], [3, 3], [1, 2]],
    row_splits=[0, 3, 4, 6])
print(rt)
print("Shape: {}".format(rt.shape))
print("Number of ragged dimensions: {}".format(rt.ragged_rank))

<tf.RaggedTensor [[[1, 3], [0, 0], [1, 3]], [[5, 3]], [[3, 3], [1, 2]]]>
Shape: (3, None, 2)
Number of ragged dimensions: 1

8.3 替代row-partitioning方案

RaggedTensor类使用‘row_splits’作为主要机制来存储关于如何将值划分为行的信息。然而，RaggedTensor还提供了对四种可选的行分区方案的支持，根据数据的格式化方式，这些方案使用起来更方便。在内部，RaggedTensor使用这些额外的方案来提高某些上下文中的效率。

行长度（Row lengths）：‘row_lengths’是一个形状为‘[nrows]’的向量，它指定每行的长度。
行起点（Row starts）：‘row_starts’是一个形状为‘[nrows]’的向量，它指定每行离起点的偏移值。等价于’row_splits[:-1]。
行限制（Row limits）：‘row_limits’是一个形状为’[nrows]‘的向量，它指定每行停止偏移量。等价于’row_splits[1:]’。
行索引和行数（Row indices and number of rows）：’ value_rowids ‘是一个形状为’ [nvals] ‘的向量，与值一一对应，指定每个值的行索引。特别是，行“rt[row]”由“rt.values[j]”组成，它里面”value_rowids [j] = =行”。\ ’ nrows ‘是一个整数，它指定了’ RaggedTensor’中的行数。特别是，’ nrows '用于表示尾随的空行。
举个例子，下面这个不规则张量等价于：

values = [3, 1, 4, 1, 5, 9, 2, 6]
print(tf.RaggedTensor.from_row_splits(values, row_splits=[0, 4, 4, 7, 8, 8]))
print(tf.RaggedTensor.from_row_lengths(values, row_lengths=[4, 0, 3, 1, 0]))
print(tf.RaggedTensor.from_row_starts(values, row_starts=[0, 4, 4, 7, 8]))
print(tf.RaggedTensor.from_row_limits(values, row_limits=[4, 4, 7, 8, 8]))
print(tf.RaggedTensor.from_value_rowids(
    values, value_rowids=[0, 0, 0, 0, 2, 2, 2, 3], nrows=5))

<tf.RaggedTensor [[3, 1, 4, 1], [], [5, 9, 2], [6], []]>
<tf.RaggedTensor [[3, 1, 4, 1], [], [5, 9, 2], [6], []]>
<tf.RaggedTensor [[3, 1, 4, 1], [], [5, 9, 2], [6], []]>
<tf.RaggedTensor [[3, 1, 4, 1], [], [5, 9, 2], [6], []]>
<tf.RaggedTensor [[3, 1, 4, 1], [], [5, 9, 2], [6], []]>

不规则张量类定义了可以用来创建每个行分隔张量（row-partitioning tensors）的方法：

rt = tf.ragged.constant([[3, 1, 4, 1], [], [5, 9, 2], [6], []])
print("      values: {}".format(rt.values))
print("  row_splits: {}".format(rt.row_splits))
print(" row_lengths: {}".format(rt.row_lengths()))
print("  row_starts: {}".format(rt.row_starts()))
print("  row_limits: {}".format(rt.row_limits()))
print("value_rowids: {}".format(rt.value_rowids()))

 values: [3 1 4 1 5 9 2 6]
  row_splits: [0 4 4 7 8 8]
 row_lengths: [4 0 3 1 0]
  row_starts: [0 4 4 7 8]
  row_limits: [4 4 7 8 8]
value_rowids: [0 0 0 0 2 2 2 3]

	注意：tf.RaggedTensor.values和tf.RaggedTensors.row_splits是属性，而剩下的row-partitioning是方法。这反映了一个事实，即row_splits是主要的底层表示，而其它行分区（row-partitioning）张量必须计算。

下面是不同的行分区方案的一些优点和缺点:
- 高效索引:row_split、row_started和row_limits方案都支持将时间常量（constant-time）索引转换为不规则张量。value_rowids和row_length方案则没有。
- 较小的编码大小:value_rowids方案在存储有大量空行的不规则张量时更有效，因为张量的大小只取决于值的总数。另一方面，其他四种编码在存储具有较长行数的不规则张量时更有效，因为它们每一行只需要一个标量值。
- 高效连接:row_length方案在连接不规则张量时更高效，因为当两个张量连接在一起时，行长度不会改变(但是行分割和行索引会改变)。
- 兼容性:value_rowids方案与tf.segment_sum等操作使用的分段格式匹配。row_limits方案与tf.sequence_mask等ops使用的格式匹配。