云控制系统下基于坡度信息的重型卡车预测性巡航控制（中文）

云控制系统下基于坡度信息的重型卡车预测性巡航控制

摘要： 重型卡车云端预测巡航控制（CPCC） 凭借云控制系统（CCS） 快速计算和地图资源的优势，在提高能源效率方面具有巨大潜力，对实现国家碳中和目标具有重要意义。 然而，大多数研究集中在车载预测巡航控制（PCC）系统上，缺乏对CCS下CPCC架构的研究。 此外，现有PCC算法存在控制目标单一、计算复杂度高等问题，阻碍了控制效果的提高。 本文提出一种基于CCS的分层架构，有效解决CPCC系统的实时计算及其算法在车云上的部署。 此外，基于动态规划原理和提出的道路点分割方法（RPSM），设计了PCC算法，利用坡度信息来优化重型卡车的速度和档位。 仿真结果表明，CPCC系统能够通过坡度预测自适应控制车辆行驶，与定速巡航相比节油率为6.17%。 而且，与其他同类算法相比，PCC算法可以通过档位和转速的协同优化，使发动机更多地运行在高效区。 而且，RPSM算法可以提前重新配置道路，路点减少率达到91%，显着降低算法复杂度。 因此，本研究对于重卡经济行驶和CPCC系统的推广具有重要的研究意义。

1. Introduction

随着移动通信技术和云计算的快速发展，云控制系统（CCS）及其应用的研究已成为重要的研究范围[1-5]。 在智能网联汽车（ICV）领域，基于云的预测巡航控制（CPCC）系统可以通过云平台获取道路和交通信息，并通过无线通信对车辆进行预测控制。 这种控制方法可以显着提高驾驶的安全性和燃油效率，这对于实现国家碳中和目标也具有重要的研究意义[6]。 对于重型卡车来说，基于坡度信息的预测巡航控制（PCC）算法是提高燃油效率、降低运输成本的重要手段[7,8]。 然而，目前星载PCC算法存在计算实时性差、地图更新困难、应用成本高等问题，严重阻碍了其推广应用。 由于CCS具有超强的计算能力和数据资源，基于CCS的PCC研究是解决上述问题的有效方法[9]。
CCS的研究大多集中在智能农业、自动化工厂、智能交通系统（ITS）、智能网联汽车（ICV）等方面。早期，这些应用都源于对网络控制系统方法的研究。 后来，随着人工智能和云计算的发展，CCS的研究在各个领域都取得了快速进展[10]。 在智能农业领域，Khattab等人。 文献[11]提出了一种基于物联网云平台的农作物智能控制的精准农业云控制架构。 所提出的三层架构具有一定的性能优势，但尚未对其有效性进行实际验证。 埃泰比等人。 文献[12]提出了一种以智慧农业为信息物理系统（CPS）的智能灌溉CCS，并通过实验验证了该系统的可行性。 在自动化工厂领域，Hu 等人。 文献[13]提出了一种基于边缘计算和云服务理论的智能机器人工厂CCS架构，显着提高了生产力。 陈等人。 文献[14]基于CPS阐述了智能工厂的定义、架构和应用案例，为智能工厂的优化设计提供了新的解决方案。 在 ITS 和 ICV 领域，Xia 等人。 文献[15]设计了一种基于CCS原理的智能交通信息物理控制系统。 仿真结果表明该系统提高了交通控制系统的动态性能。 基于CPS理论，Li等人。 文献[6]提出了我国智能网联汽车CCS架构，并将其命名为车路云一体化控制系统，致力于连接智能交通和智能网联汽车两大领域，旨在加速我国智能汽车的发展。 上述研究不仅包括CPS在各个领域的创新探索，也包括在特色子领域的具体应用，但对于CCS下的CPCC系统架构研究较少。
利用坡度信息的预测巡航控制算法的控制方法可分为三类：最优控制[16-18]、模型预测控制（MPC）[19-21]和瞬时控制[22,23]。 动态规划（DP）基于最优控制理论，在处理PCC规划问题时总能产生最省油的结果。 赫尔斯特罗姆等人。 文献[24,25]提出了一种基于DP的前瞻控制算法，利用车辆前方道路坡度信息对重型柴油卡车进行最小节油控制。 丛等人。 [26]利用预先学习到的道路拓扑信息构建基于DP的最优换挡策略，旨在实现重卡燃油最小化的目标。 与最优控制相比，MPC可以通过滚动时域优化来提高系统的鲁棒性，这在PCC中得到了广泛的研究。 文献[27,28]基于道路坡度信息，构建并求解了以燃油经济性为目标的MPC控制问题，仿真结果表明所开发的系统可以显着降低车辆燃油消耗。 然而，最优控制算法和MPC在求解最优控制问题时计算复杂度高、实时性差。 因此，一些研究人员尝试使用瞬时控制方法来设计节油算法。 例如，徐等人。 文献[29]仅根据当前道路坡度信息设计了燃油经济性优先的反馈控制器，大大减少了计算时间。 然而，瞬时控制仅根据当前行驶工况对车辆动力系统进行优化，没有预测能力，在节油方面比最优控制和MPC差[30]。
尽管现有的研究对基于坡度信息的PCC算法的设计做出了很大的贡献，但仍存在一些不足。 一方面，大多数学者研究的PCC算法仅考虑车辆速度或档位的单一优化，很少有人同时优化两个控制目标，以满足车辆在不同行驶条件下的动力性和经济性要求，这一点显得尤为重要 适用于在斜坡上行驶的重型卡车。 另一方面，大多数研究人员通过添加约束或简化目标函数来优化PCC算法的计算复杂度。 但很少有人从道路分割的角度来降低算法的维度。
鉴于此，在ICV CCS下，本文提出了CPCC系统的分层架构。 此外，基于动态规划原理和道路点分割方法（RPSM），提出了一种新颖的PCC算法。 与现有研究相比，本工作有两个显着贡献：
(i) CPCC 系统的分层架构。 该架构可以实现地图的便捷获取和智能网联汽车群体的协同管理，有利于PCC算法的产业化推广。
(ii) 一种新颖的 PCC 算法。 该算法可以利用预测的坡度信息来优化速度和档位，同时考虑车辆的经济性和动态性，并通过RPSM降低算法的计算复杂度。
本文的结构如下。 第二节设计了CPCC的系统架构。 在第 3 节中，构建了车辆模型。 第四节介绍了CPCC系统的算法和原理。 第 5 节提供了模拟和分析。 最后，第 6 节总结了结论。

2. System architecture of CPCC

ICV CCS的通用架构已经提出多年[6]，但该架构并不是一成不变地适用于不同的应用，需要进行调整和重新设计。 本章介绍了智能网联汽车CCS的总体架构。 然后，在总体架构的基础上，设计了CPCC系统的分层架构。

2.1 General architecture of the ICV CCS

该总体架构也称为车路云综合控制系统，是以云控制平台（CCP）为核心、面向智能网联汽车和交通运输的综合控制系统[6,9]。 该架构由CCP、路侧基础设施、通信网络、智能网联汽车及相关支撑平台组成。 其整体架构如 图1 所示。

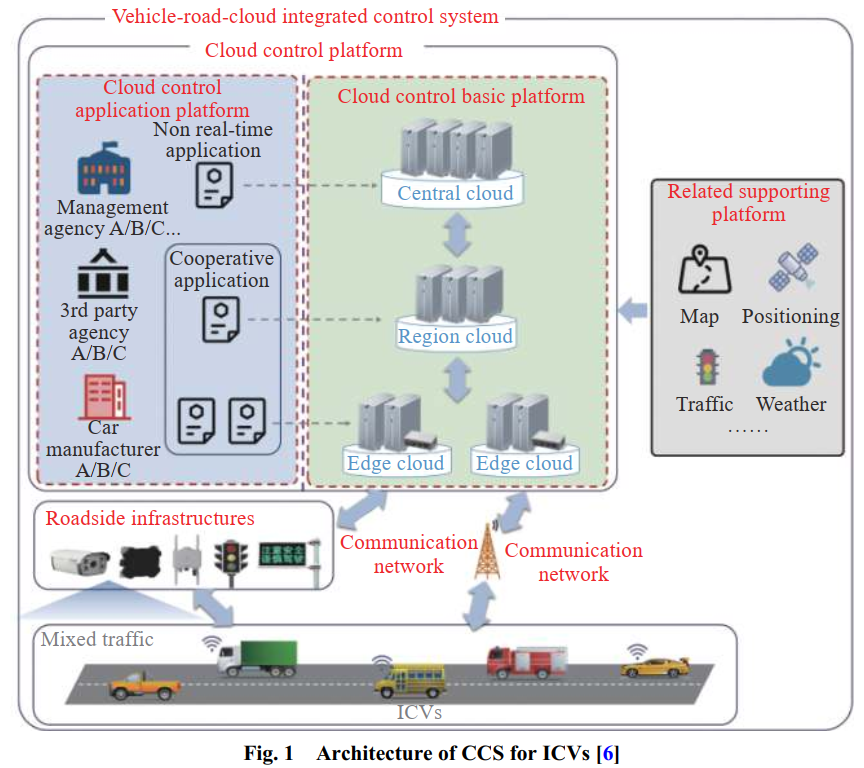
CCP旨在构建实时计算环境，整合车路云数据，协同应用在智能网联汽车和交通性能优化中，分为云控基础平台和云控应用平台。 基础平台提供实时交通数据和协同应用的应用环境。 为了更好地支持不同应用的服务需求，CCP分为边缘云、区域云和中心云。 边缘云通常运行实时协作应用程序，区域云运行近实时协作应用程序，国内中央云服务运行非实时应用程序。 三层云相互协调，从下到上实时服务逐渐减少，服务量依次增加。 在应用平台中，根据各个机构对应用的需求，有管理机构、第三方机构和汽车制造商。 交通中的智能网联汽车通过通信网络或路边通信单元与云端进行交互。 路侧传感单元实时感知道路交通数据并上传至边缘云进行应用处理。 相关支撑平台为中共提供地图、交通等数据支持。
PCC 需要快速计算和实时的路线图数据。 凭借CCS的优势，将其置于智能网联汽车CCS中将进一步增强其控制效果。 PCC算法布置在边缘云上，根据车辆巡航的信号，通过调用地图，快速完成控制命令的实时求解。 区域云可以预测区域内的交通状况信息，实现区域宏观交通调控。 中央云主要致力于PCC的非实时应用分析和车辆管理任务，用于管理车辆配置参数和PCC运行数据。 通过对一段时间的运行数据进行大数据分析，可以实现一些应用，比如PCC算法的持续优化、用户驾驶习惯的分析、节油统计等。 以PCC为例介绍各级CCS的功能和优势，可以展示基于云的预测巡航系统及其架构的研究意义。 因此，在ICV CCS下，CPCC系统的分层架构设计在2.2小节中描述。

2.2 Design of layered architecture for CPCC system

CPCC系统的实现需要对云端和车载功能进行合理分析，确保有效利用各自优势，实现系统高效、安全运行。 为了降低车载Telematics BOX（T-BOX）的硬件成本，车载平台主要解析云端发送的控制命令，并根据设定的状态转换条件监控车辆的巡航状态，从而 发送和接收控制命令并安全地切换巡航模式。 CPCC系统的分层架构如下 图2 所示。

CPCC系统主要由地图服务模块、RPSM算法、PCC算法、T-BOX和控制器单元组成，如图2所示。CCP配备了受控车辆的发动机型号和动态参数，以及通过边缘云实时获取车辆的GPS位置、参考速度、档位等参数。 这些数据存储在云控基础平台上，等待PCC算法的使用。 云控应用平台为PCC算法提供快速计算环境，并根据需要获取基础平台的数据。 车载平台主要由T-BOX和控制器单元组成，用于云控制指令的分析和控制。 T-BOX内部与控制器局域网(CAN)总线连接，外部通过无线通信与CCS连接。 命令解析模块用于定位并提取控制序列并将其发送给控制单元执行。 巡航状态控制是根据设定的状态转换逻辑，以安全为目标来控制巡航状态。 此外，车辆运行数据通过T-BOX上传至云端，供应用平台对数据进行统计分析。
T-BOX中的巡航状态控制逻辑对GPS信号质量、网络状态、数据格式、车辆速度和巡航开关信号进行识别，以确定是否满足状态转移条件，确保系统安全运行。 变换逻辑图如图3所示。 条件如表 1 所示。

3. Vehicle model

整车模型主要包括发动机模型、变速器模型和纵向动力学模型。 本节介绍下面PCC算法所需的车辆模型，并对模型进行部分简化。 本文研究的卡车样机如图 4 所示，卡车的主要参数如表 2 所示。由于部分参数涉及企业机密，因此仅公布与本文算法相关的典型参数，其他参数仅给出参考范围。

3.1 Engine model

根据某型柴油机的通用特性数据构建发动机模型，包括发动机转速、扭矩、燃油消耗率三列数据。 基于线性插值原理（节气门开度约等于扭矩百分比），将发动机MAP数据生成为发动机燃油消耗率和输出扭矩两个函数，如（1）所示。

其中 ${\omega }_e$ 为发动机的输出转速，$\alpha$ 为节气门开度。 式（1）表明，三个变量 ${\omega }_e$、$\alpha$ 、$T_e$ 之间存在函数关系，可以通过变形转化为 $\alpha =throttle({\omega }_e,T_e)$。 那么，(1)可以表示为

式（2）可通过发动机的转速和扭矩计算燃油消耗量。

3.2 Driveline model

车辆的动力传递路线如 图5 所示。发动机的转速和扭矩经过传动系统后传递到驱动轮。 由于离合器、变速器等传动系统部件均为刚性联轴器，扭转变形可以忽略不计。

根据文献[25]和[31]，为了便于传动系统模型的分析计算，传动系统的总转动惯量可以等效到轮胎，记为 $J_t$ 。 因此，当设定变速器档位时，发动机扭矩通过(3)和(4)传递至车轮。

其中 $T_c$ 是传递到离合器的扭矩， $T_w$ 是传递到轮胎的扭矩。$i=i_g{i}_0$ 和 $\eta ={\eta }_g{\eta }_0$ 分别是传动系统的总传动比和总效率。
那么，传递到车轮 $F_w$ 的牵引力可以表示为(5)。

其中 ${\dot{\omega }}_w$ 是发动机曲轴的角加速度。
此外，发动机速度通过传动系统转换为行驶速度，如(6)所示。

3.3 Longitudinal dynamics model

车辆行驶受力分析如图6所示。

根据牛顿第二定律和传动系统模型，车辆行驶平衡方程可表示为（7）[31]。

将式（3）−（6）代入式（7），得到车辆纵向动力学模型，如式（8）所示。

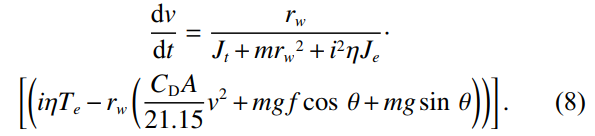
4. Algorithm and principle of CPCC system

本节介绍了使用DP构建PCC算法的方法，并从道路数据预处理的角度提出了RPSM算法来降低DP算法的复杂度，从而实现CPCC系统的快速计算。 基于DP的PCC算法主要研究DP的代价函数项、约束条件以及降维优化。

4.1 PCC algorithm based on DP

PCC算法是利用车辆前方路面坡度信息来求解档位和车速的最优控制序列。 然后，通过执行预测控制序列来实现车辆的预测巡航控制。

4.1.1 Cost function

由于PCC算法的状态空间根据距离域划分为阶段，因此通过离散积分来计算成本函数方程[25]。 成本函数包括油耗、巡航参考速度偏差、变化率、换挡惩罚和节气门开度比较 五项，如式(9)所示。

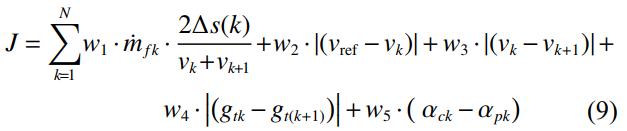
式中，${\dot{m}}_{fk}$为 k 阶段的燃油消耗率。
变量 ${\alpha }_{pk}$ 和 ${\alpha }_{ck}$ 分别表示 PCC 和 CC 控制中在状态 k 转移所需的节气门开度。
利用油耗惩罚因子保证车辆行驶的燃油经济性； 速度偏差惩罚因子用于限制规划速度尽可能接近参考速度，以保持速度不偏离参考速度过大； 利用速度变化率惩罚因子来约束两阶段的速度变化，减少急加速和急减速，以节省燃油消耗； 采用档位惩罚惩罚系数来减少前后级变速传动中的跳档现象； 通过对比CC节气门开度，节气门开度惩罚因子尽可能减少了大节气门开度的现象。

4.1.2 Constraints

为了避免车辆速度偏离参考速度过大，状态空间的速度边界设置如下：

根据发动机通用特性图，发动机的有效工作区往往在一定的发动机转速和扭矩范围内，因此存在以下约束：

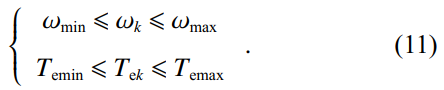
根据经济驾驶原理，快速加减速会对车辆的燃油消耗产生很大影响，因此存在加速度约束。

其中 s 是驾驶位置。
在DP的状态空间中，有最低巡航档位和最高巡航档位。 而且，在发动机转速和车速的限制下，只能使用特定的变速档位。 因此，如下的齿轮约束是必不可少的。

4.1.3 Determination of optimal control sequence

为了通过DP求解PCC问题的最优解，首先需要根据控制变量建立DP的状态空间。 那么，使成本函数最小的状态序列就是前方道路预测驾驶的最优控制序列。 基于DP的PCC算法的状态空间和计算流程如图7 所示。

图7 给出了由速度和档位构建的状态空间，在约束下只有部分状态点满足要求，以减少不必要的计算。 通过反方向计算(9)，最终从正方向得到预测范围内的最优速度和档位序列。
DP的阶段是根据道路点之间的距离来划分的。 因此，在预测距离固定的情况下，如果间距太小，则DP的计算复杂度较大，实时性较差。 因此，道路点的预处理对于DP的降维优化具有重要作用。

4.2 Dimensional reduction optimization of DP by RPSM

CPCC系统中DP的求解复杂度主要由预测距离、可用档位数、约束范围和速度离散区间决定。 DP的计算时间会影响系统的迭代控制精度。 RPSM算法的原理是在不改变预测距离的情况下减少DP的阶段数。 例如，如果预测距离为2 km，原始道路点间隔为20 m，则PCC算法需要100阶段的状态空间才能通过DP求解一次。 如果将2公里按照一定规则分为10个阶段，计算时间可减少10倍，大大减少系统闭环跟随控制时间。 RPSM算法流程图如 图8 所示。

RPSM是道路信息的预处理算法，输出分割后的坡度和道路点间隔信息，作为PCC算法的输入。 首先将从地图服务器中提取的道路信息进行清洗和重新处理，将其格式转换为RPSM算法所需的接口格式。 其次，根据道路点的顺序，基于三种分割条件进行迭代计算。 条件1：$|\Delta Angel|>\theta$ 是斜率约束 。 在道路点的迭代过程中，如果两个原始道路点的坡度变化超过 $\theta$，则在该点进行分割。 条件2：$|Sa|>\beta$ 为累积斜率约束，用于在不满足条件1时判断累积斜率值 $Sa$ 是否满足分割要求。 条件3：$Si>\gamma$ 是道路点间距的约束，表示一次分割后，当原道路点的累计距离超过 $\gamma$ 时，进行分割。 在迭代分割过程中，首先判断条件1，然后判断条件2和条件3，直到完成道路序列循环。 最后根据PCC算法要求的格式输出分割后的路点序列。

4.3 Control method and process of CPCC system

CPCC系统采用迭代更新和滚动距离域优化的控制方法。 当CPCC模式启动时，根据一定的距离阈值重新计算最佳速度和档位。 详细控制流程如图9所示。

步骤1 ：当云平台检测到车辆和T-BOX各信号均满足进入CPCC系统的要求时（详见第三节车辆平台介绍），将激活CPCC模式以取代CC模式。
步骤2 ：如果当前初始速度 $v_0\le v_{max}$，则按照最小设定值规划推荐速度和档位。 反之，如果初始速度大于最大值，则输出设定的档位和速度最大值。
步骤3 ：当满足 $v_{min}⩽v_0⩽v_{max}$ 条件时，云端接受车辆的位置信息，并从地图服务器中提取当前道路前方 $X$ 公里的地图数据（远距离）。
步骤4 ：当获取的道路数据范围 $X$ 大于优化范围 $Y$ 时，说明地图数据缺失，应退出CPCC模式，否则运行并进入步骤5。
步骤5 ：通过RPSM算法对 $X$ km道路进行分段。 然后，根据车辆当前位置，得到 $Y$ km的分段道路，以在当前预测范围内优化最优控制策略。
步骤6 ：根据速度、档位和预测距离****构建DP的状态空间。
步骤7 ：根据DP的迭代计算原理，在约束范围内从后向前计算成本函数，最终得到最小成本路径。 然后，获得最佳速度和档位序列。
步骤8 ：根据车辆的实时位置，在最优控制序列中找到相应的速度和档位控制命令，并将其发送至车辆控制器单元。
步骤9 ：判断一个迭代周期内车辆的续驶里程是否超过 $r$ m 。 如果不是，则仍然按照步骤6发送优化控制指令。如果是，则进行下一次迭代，并返回步骤2。

5. Simulation and analysis

模拟实验分为两部分。 首先，通过实际道路验证RPSM的分割效果。 然后，利用同一道路对基于Matlab/Simulink和Trucksim建立的CPCC系统仿真模型进行仿真。

5.1 Effect verification of the RPSM algorithm

选择的模拟道路为中国山东G22高速公路上的沂源服务器至诸葛服务器36公里。 该道路坡度和高程变化较大，满足验证需要。
该道路鸟瞰图如图10所示

基于RPSM算法对该道路进行离线预处理，分割效果如图11所示。在道路高程图上展示了原始道路点和分割道路点，在道路高程图的某些关键位置显示了局部分割效果。 可以看出，分割后的道路点基本保留了坡顶和坡底位置原始道路点的特征信息。 从整体上看，将原来共有1731个点的道路合理划分为155个，道路点减少率为91%，如图12所示。


RPSM算法的优点是不仅大大减少了道路路段数量，而且很好地保留了道路特征点。 因此，可以在不增加时间维度的情况下延长CPCC系统的道路预测距离。 此外，通过将该算法与CPCC系统相结合，可以极大地释放CCP的计算能力，并可以进一步扩大CCS管理的配备PCC的车辆数量。

5.2 Simulation analysis of CPCC system

CPCC系统是在CCS的基础上结合了PCC和RPSM算法。 采用与5.1节相同的实验道路来验证其控制有效性。

5.2.1 Simulation model

仿真模型如图13 所示，包括四个模块。 模块1为地图更新模块，包含原始地图数据和RPSM算法，能够向PCC算法提供分段地图数据。 模块2是PCC算法求解器，它使用预测的坡度信息根据DP原理求解最佳档位和速度。 实际上，模块2位于CCP的边缘云上，满足实时计算和命令下发的需求。 模块3用于模拟车辆端T-BOX的控制指令解析功能，可以根据车辆的行驶位置提取预测控制序列中的控制命令。 模块4是Trucksim S-function，通过配置车辆参数和道路信息来模拟车辆在实际道路上的行驶过程。 四个模块连接形成闭环，模拟分层架构下CPCC系统的计算和控制过程。

5.2.2 Parameter setting

代价函数权重的调试大致分为三个步骤。 第一步，分析各参数对油耗的趋势影响，找出对油耗影响明显的几个成本项目。 第二步是通过控制变量的方法确定各参数的大致边界范围。 第三步，以油耗、换挡频率、变速率等为评价目标进行权重调试。 根据上述调试方法，权重设置如表3所示。

CPCC系统仿真参数设置如表4所示。

5.2.3 Results analysis

通过Trucksim与Simulink的联合仿真，对搭载CPCC系统的重卡进行了真实道路上的仿真验证。 CC模式和经典的DP速度搜索算法（DP-V）分别作为比较算法（DP-V是[32]中经典的基于DP的速度搜索算法的自定义缩写）。 参考速度、卡车型号、路况与CPCC系统相同。 仿真结果总图如图14所示，它显示了完整道路的仿真结果。 图 15（a）和图 15（b）给出了图 14 中截取的 0−10 km 和 25−32 km 典型断面结果，以便对规划效果进行详细对比分析。



如图14所示，与CC和DP-V相比，CPCC系统可以适度调节车速并预测性降档。 与DP-V明显不同的是，PCC算法规划的速度曲线相对平滑得多，行驶稳定性更好。 而且，PCC算法还通过调整最佳档位来保证坡道行驶的动态性能，这对于重卡尤为重要。 DP-V算法可以通过优化速度来达到节油的目的，与CC相比节油率为3.74%。 但由于DP-V没有考虑档位优化，经常出现油门全开的情况，会造成燃油燃烧不充分，污染增加。 这也是DP-V的节油率低于PCC的重要原因。 总体而言，在行驶时间大致相等的情况下，PCC算法表现出比CC和DP-V更高的坡道适应性，并且与CC相比获得了6.17%的节油率。 具体仿真结果如表5所示。
图15（a） 中，卡车在0.5公里和7.5公里处下长坡时，提前减速以避免高速冲击。 在1.9公里至4.6公里的上坡和下坡行程中，卡车通过降档并保持11档的档位来维持动力和辅助制动。 通过车速和档位的调整，前10公里路段比CC节油率为4.9%。 另外，虽然DP-V的调速范围比PCC更明显，但DP-V的节油效果并不比CC好。 相反，PCC算法通过档位和车速的协同优化表现出了良好的性能。
从图15（b） 可以看出，车辆在爬26.5公里长上坡时，提前在坡底降档，匀速爬坡，避免了换挡带来的能量损失。 坡道中间，符合节油行驶规律。 此外，CPCC的节气门开度明显低于CC，全程节油率达到14.3%，充分体现了档位预测的重要性。 通过分析速度曲线可以发现，在长上坡情况下，三种算法的速度调节能力都受到限制。 而PCC算法通过预测挡位调整，同时提高了动态性能和经济性，这是一个明显的优点。
上面对仿真结果进行了曲线分析，下面将进行控制效果的机理分析。 通过对CC、DP-V、CPCC模式下发动机转速、扭矩和燃油消耗率进行统计计算，得到三种模式下发动机工作区间分布，如图16−18所示。
对比图 16和图 18可以发现，CC模式下发动机负荷在40%~80%范围内的燃油比例和工作时间分别超过74%和57%，显着提高。 高于 CPCC 模式。 另外，CC模式下，发动机节气门开度接近100%的工作时间明显高于CPCC模式，且多发生在重载爬坡工况下。 这种情况会导致发动机工作不良，燃烧不充分，不利于延长发动机及其附件的工作寿命。 如图 17 所示，在 DP-V 模式下，发动机的工作范围比 CC 模式明显移至高效区（高效转速范围为[1200 1400]），这是其与CC模式相比更省油。 但在60%−100%范围内发动机负荷的工作时间和燃油比例分别为42.21%和62.65%，明显高于CPCC模式。 而且，这种情况下，虽然转速范围偏向高效区，但发动机的有效负载范围（高效发动机负载范围为[40% 60%]）明显小于CPCC模式。



综合以上分析，可以充分说明PCC算法比CC和DP-V模式具有更强的通过档位和转速协同优化调整发动机移至高效率区的能力，从而减少降低油耗，提高重卡综合性能。

6. Conclusions

本文提出了一种基于智能网联汽车CCS的CPCC系统分层架构，合理安排了整车平台和CCP上的PCC算法。 为了同时满足重卡坡道行驶时的动力性和节油要求，提出了一种基于DP的车速与档位协同优化的PCC算法。 此外，从道路点分割的角度出发，提出了RPSM算法来降低DP算法的维数，从而降低PCC算法的计算复杂度。 仿真结果表明，RPSM算法将原道路点1731个减少到155个，道路点减少率为91%。 同时，分割后的道路很好地保留了道路特征信息，可以减少PCC算法的计算误差，保证精度。 对CPCC系统进行仿真可以发现，所提出的PCC算法能够根据坡度的变化自适应调整车速和档位，相比CC模式节油率为6.17%，能够满足不同坡道工况下重型卡车的动力性和经济性表现。 另外，与DP-V的同类算法相比，PCC算法可以通过档位和转速的协同优化，使发动机更多地运行在高效区。 因此，本文提出的CPCC系统和架构能够满足算法的快速可计算性，并具有较高的节油能力，对于智能网联汽车CCS的工业化应用具有很强的前景。
由于仿真模型的限制，本文没有对CPCC系统中的巡航状态转换逻辑进行验证。 未来，该系统将部署在云控制平台上，并将状态转换逻辑嵌入到T-BOX中，完成实车验证。 此外，还将增加CPCC与人类驾驶员的对比实验，以充分验证算法的有效性。