负反馈放大电路分析

原创已于 2024-05-11 17:25:23 修改 · 4k 阅读

26 ·

CC 4.0 BY-SA版权

文章标签：

#硬件工程

于 2024-04-25 17:23:35 首次发布

模拟电路专栏收录该内容

2 篇文章

订阅专栏

一、负反馈放大电路简介

负反馈放大电路包括前馈通路和反馈通路，其中反馈通路在输出端采集电压或电流信号，乘以反馈系数后与参考输入作差分。负反馈放大电路的结构与负反馈控制系统相似，如下图所示，主要包括前馈网络H(s)、反馈网络G(s)、输出采集和输入差分。负反馈结构以增益为代价，提升放大电路的带宽、线性度、底噪，并调整输入阻抗、输出阻抗等性能指标。

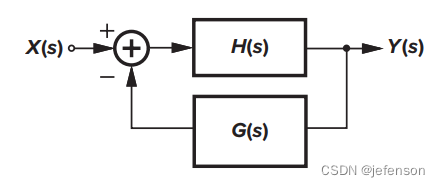
当输入信号是电压信号时，输入差分需要双端口，比如将输入信号接MOS管的栅极，反馈输出信号接MOS管的源极，实现微弱电压的放大；当输入信号是电流信号时，输入差分需要一个网络节点，节点分别连接至输入信号，反馈信号和三极管基极，输入电流与反馈电流差分后进入三极管的基极，实现微弱电流的放大（注意运算放大器有虚短和虚断特点，可以用于电压差分，也可以用于电流差分）

负反馈放大电路的输出与输入的关系：

$\frac{Y\left ( s \right )}{X\left ( s \right )}=\frac{H\left ( s \right )}{1+G\left ( s \right )\cdot H\left ( s \right )}$

假设前馈网络和反馈网络与频率无关（例如只考虑低频），前馈增益和反馈增益退化为A和 $\beta$ ，此时输出与输入的关系：

$\frac{Y}{X}=\frac{A}{1+\beta\cdot A}$

当 $\beta\cdot A\gg 1$ 时， $\frac{Y}{X}=\frac{1}{\beta}$ 。

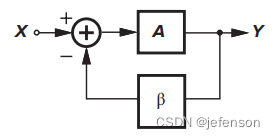
$\beta\cdot A$ 在负反馈放大电路中也称为环路增益，环路增益是影响性能指标的关键因素，通过将输入信号X置0，断开反馈网络输入端，并施加激励信号X，可得 $Y=-\beta A\cdot X$ ，但由于反馈网络存在有限的输入阻抗和输出阻抗，实际的开环增益和环路增益会受到影响。

二、负反馈放大电路的种类

根据输入信号和输出信号分别是电压信号或电流信号，可以将放大电路分成电压放大（电压到电压）、跨阻放大（电流到电压）、跨导放大（电压到电流）和电流放大（电流到电流）。四种常见的放大电路如下图所示：

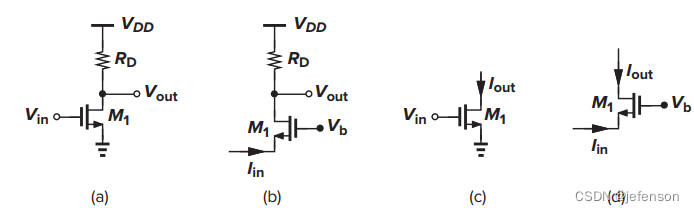
对于负反馈放大电路，前馈网络可以是四种放大电路中的任意一种，反馈网络则与之相反，例如，当前馈网络是跨阻放大时，反馈网络是跨导放大。于是，负反馈放大电路根据输出信号类型和输入信号类型，可以分成电压-电压、电流-电压、电压-电流和电流-电流。

三、二端口网络模型

二端口网络模型是仅包含单输入和单输出两个端口的网络模型，根据输入输出的受控信号源类型，二端口网络模型可以分为Z模型、Y模型、H模型和G模型等。

①Z模型：受控信号源是输入电流和输出电流，最简单的Z模型是电流采样电路，受控信号源是输入电流，需要计算输出电压，由于负载开路时，输出电流为0，实际上受控信号源仅输入电流，即 $V_{1}=V_{2}=r\cdot I_{1}$

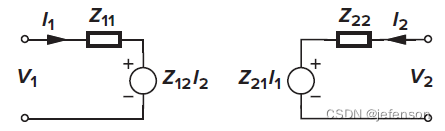
Z模型的表达式如下：

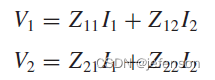
②Y模型：受控信号源是输入电压和输出电压

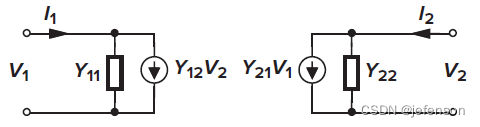
Y模型的表达式如下：

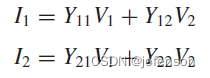
③H模型：受控信号源是输入电流和输出电压，常见案例是三极管，输出电流与输入电流和输出电压有关，即 $I_{C}=\beta \cdot I_{B}+\frac{V_{C}}{r_{o}}$

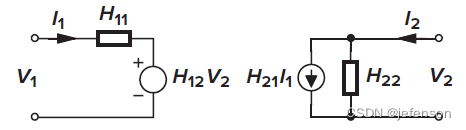
H模型的表达式如下：

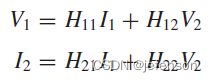
④G模型：受控信号源是输入电压和输出电流。常见案例是MOS管，输出电压与输入电压和输出电流有关，即 $V_{o}=-g_{m}\cdot r_{o}\cdot V_{i}+I_{D}\cdot r_{o}$ ；最简单的G模型是分压电路，由于负载开路时，输出电流为0，实际上受控信号源仅输入电压，即 $V_{o}=\frac{R_{s}}{R_{s}+R_{f}}\cdot V_{i}$

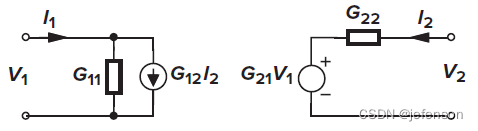
G模型的表达式如下：

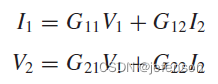
线性放大电路适用于二端口网络模型，在负反馈放大电路中，前馈网络和反馈网络都是放大电路，只是反馈网络一般结构简单，仅有输入端有受控信号源，例如电阻分压电路、电流采样电路等

四、负反馈放大电路分析

1、电压-电压负反馈

前馈网络的输入信号和输出信号是电压信号，同理反馈网络的输入信号和输出信号也是电压信号，所以前馈网络和反馈网络均使用G模型，忽略放大电路的内部反馈，则 $G_{12}=0$

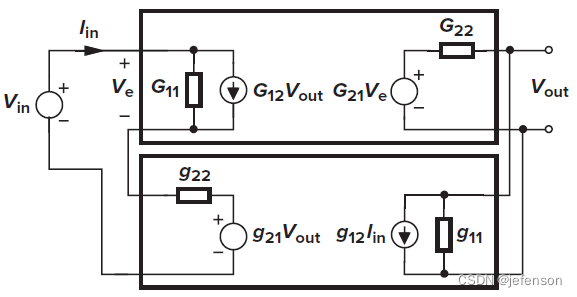
理想反馈网络的输入阻抗是无穷大，即 $g_{11}=0$ ，输出阻抗是0，即 $g_{22}=0$ ，此时，负反馈放大电路的输入阻抗是原前馈网络输入阻抗的1+Aβ倍，输出阻抗是原前馈网络输出阻抗的1/(1+Aβ)，但实际上负反馈网络的输入输出阻抗都是有限值，当输出开路时计算闭环增益：

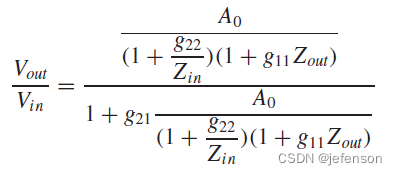
相比理想反馈网络下的闭环增益，实际反馈网络的闭环增益通过修正开环增益计算可以得到：

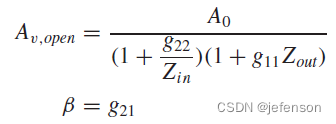
其中：

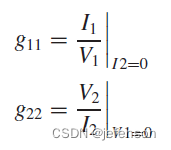
由于修正的开环增益符合输入输出的分压原则，通过修改原闭环电路，可以直接分析修正的开环增益，即将反馈网络同时纳入反馈输入端和反馈输出端，其中反馈输入端的反馈网络另一端需开路（ $I_{2}=0$ ），反馈输出端的反馈网络另一端需接地（ $V_{1}=0$ ），得到修正后的开环电路

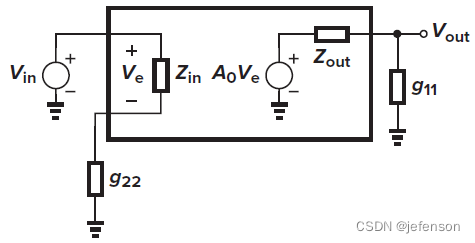
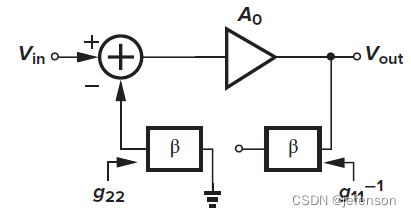
如上，对于非理想反馈网络，电压-电压放大电路的输入阻抗是修正后的开环电路输入阻抗的1+Aβ倍，输出阻抗是修正后的开环电路输出阻抗的1/(1+Aβ)，注意A是修正的开环增益

典型案例

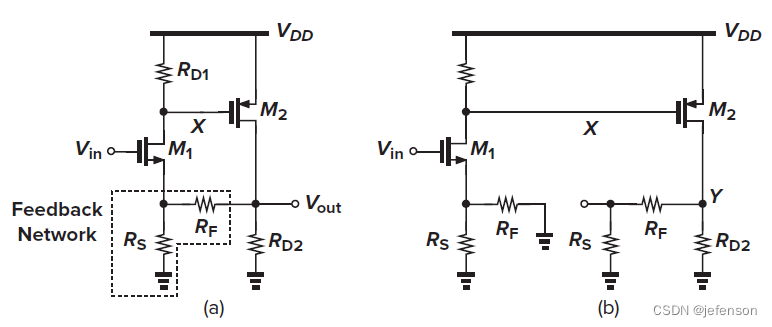
左图是典型的电压-电压负反馈放大电路，前馈网络通过两级共源极放大电路实现，反馈网络是简单的电阻分压，利用MOS管的栅极和源极实现差分输入，负反馈逻辑：M1栅极电压上升→M2栅极电压下降→M2漏极电压上升→M1源极电压上升。若不考虑输出负载对直流工作点的影响，可以按右图重构电路计算修正的开环增益，修正后的开环电路输出阻抗是 $\left ( R_{S}+R_{F} \right )\parallel R_{D2}$ ，需确保 $R_{s}+R_{f}\gg R_{D2}$ 避免开环增益和输出阻抗下降

2、电流-电压负反馈

前馈网络的输入信号是电压信号，输出信号是电流信号，而反馈网络则相反，输入信号是电流信号，输出信号是电压信号，所以前馈网络使用Y模型，反馈网络使用Z模型，忽略放大电路的内部反馈，则 $Y_{12}=Z_{12}=0$

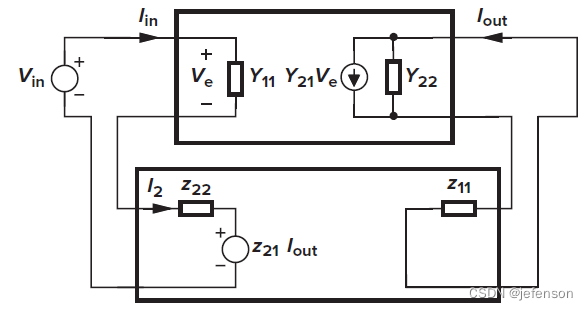
理想反馈网络的输入阻抗是0（ $Z_{11}=0$ ），输出阻抗是0（ $Z_{22}=0$ ），此时，负反馈放大电路的输入阻抗是原前馈网络输入阻抗的1+Aβ倍，输出阻抗是原前馈网络输出阻抗的1+Aβ倍，但实际反馈网络的输入输出阻抗非0，当输出短路时计算闭环增益：

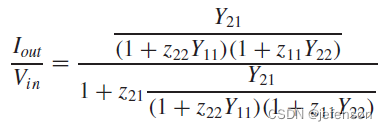
相比理想反馈网络下的闭环增益，实际反馈网络的闭环增益通过修正开环增益计算可以得到：

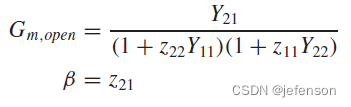
其中：

$Z_{11}=\frac{V_{1}}{I_{1}}|_{I_{2}=0}$

$Z_{22}=\frac{V_{2}}{I_{2}}|_{I_{1}=0}$

由于修正的开环增益符合输入输出的分压原则，通过修改原闭环电路，可以直接分析修正的开环增益，即将反馈网络同时纳入反馈输入端和反馈输出端，其中反馈输入端的反馈网络另一端需开路（ $I_{2}=0$ ），反馈输出端的反馈网络另一端需开路（ $I_{1}=0$ ），得到修正后的开环电路

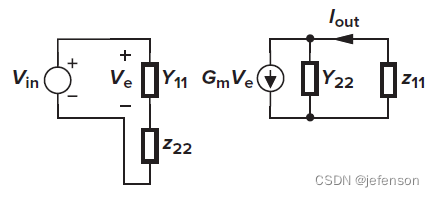
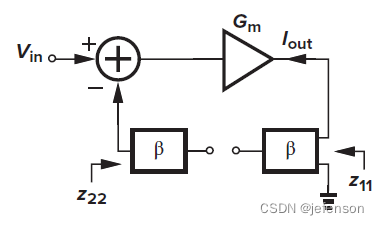
如上，对于非理想反馈网络，电流-电压放大电路的输入阻抗同样是修正后的开环电路输入阻抗的1+Aβ倍，输出阻抗是修正后的开环电路输出阻抗的1+Aβ倍，注意A是修正的开环增益

典型案例

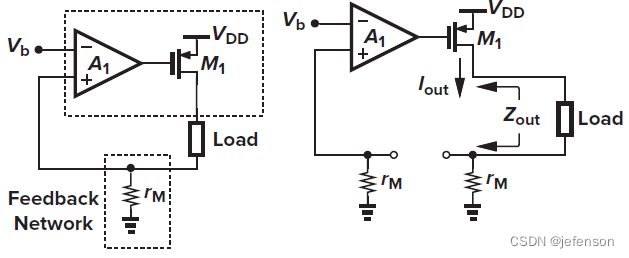
左图是典型的电流-电压负反馈放大电路（电池充电电路），前馈网络通过运算放大器和共源极放大电路实现，反馈网络是简单的电流采集电路，在运算放大器的输入端实现差分，负反馈逻辑：运放反相端电压上升→M1栅极电压下降→M1源极电流上升→运放正相端电压上升。按照右图重构电路计算修正的开环增益，根据诺顿定理，M1可等效为电流源与输出阻抗并联，输出阻抗等于 $r_{o1}+r_{M}$ ，由于负载与采样电阻串联，当 $r_{M}\ll r_{o1}$ 时，开环增益损失最小

3、电压-电流负反馈

前馈网络的输入信号是电流信号，输出信号是电压信号，反馈网络则相反，输入信号是电压信号，输出信号是电流信号，所以前馈网络使用Z模型，反馈网络使用Y模型，忽略放大电路的内部反馈，则 $Z_{12}=Y_{12}=0$

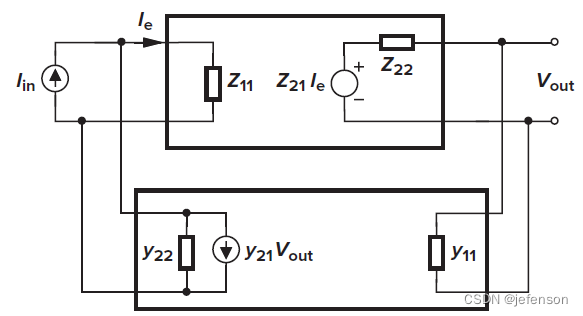
理想反馈网络的输入阻抗是无穷大（ $Y_{11}=0$ ），输出阻抗也是无穷大（ $Y_{22}=0$ ），此时，负反馈放大电路的输入阻抗是原前馈网络输入阻抗的1/(1+Aβ)，输出阻抗是原前馈网络输出阻抗的1/(1+Aβ)，但实际反馈网络的输入输出阻抗是有限值，当输出开路时计算闭环增益：

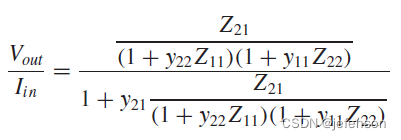
相比理想反馈网络下的闭环增益，实际反馈网络的闭环增益通过修正开环增益计算可以得到：

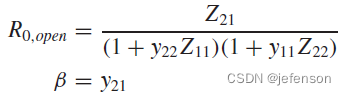
其中：

$Y_{11}=\frac{I_{1}}{V_{1}}|_{V_{2}=0}$

$Y_{22}=\frac{I_{2}}{V_{2}}|_{V_{1}=0}$

由于修正的开环增益符合输入输出的分压原则，通过修改原闭环电路，可以直接分析修正的开环增益，即将反馈网络同时纳入反馈输入端和反馈输出端，其中反馈输入端的反馈网络另一端需接地（ $V_{2}=0$ ），反馈输出端的反馈网络另一端需接地（ $V_{1}=0$ ），得到修正的开环电路

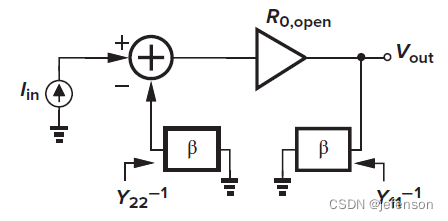
如上，对于非理想反馈网络，电流-电压放大电路的输入阻抗是修正的开环电路输入阻抗的1/(1+Aβ)倍，输出阻抗是修正的开环电路输出阻抗的1/(1+Aβ)倍，注意A是修正的开环增益

典型案例

中图是典型的电压-电流负反馈放大电路，前馈网络通过反馈电阻 $R_{F}$ 和共源极放大电路，实现跨阻放大，反馈网络通过反馈电阻 $R_{F}$ 采样输出电压（确定 $R_{F}$ 电流），负反馈逻辑：M1栅极电流上升（实际上栅极无电流，替换为三极管更易理解）→M1漏极电压下降→反馈电阻 $R_{F}$ 电流上升→M1栅极电流下降。按照右图重构电路计算修正的开环增益，修正的开环电路输出阻抗是 $R_{F}\parallel R_{S}$ ，需确保 $R_{F}\gg R_{D}$ ，避免输出阻抗和开环增益下降。令 $V_{2}=0$ ，可以计算反馈增益 $Y_{21}=I_{2}/V_{1}=-1/R_{F}$

4、电流-电流负反馈

前馈网络的输入信号和输出信号是电流信号，同理反馈网络的输入信号和输出信号也是电流信号，所以前馈网络和反馈网络都使用H模型，忽略放大电路的内部反馈，则 $H_{12}=0$

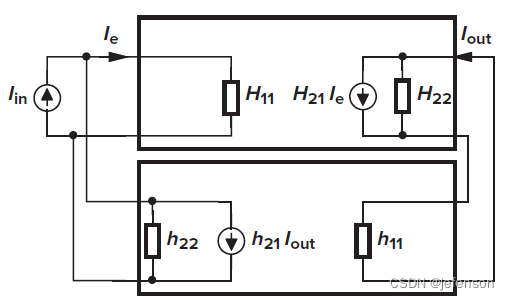
理想反馈网络的输入阻抗是0（ $H_{11}=0$ ），输出阻抗是无穷大（ $H_{22}=0$ ），此时，负反馈放大电路的输入阻抗是原前馈网络输入阻抗的1/(1+Aβ)，输出阻抗是原前馈网络输出阻抗的1+Aβ倍，但实际反馈网络的输入输出阻抗是有限值，当输出短路时计算闭环增益：

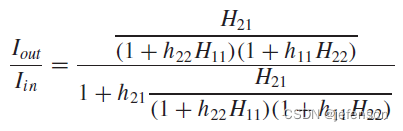
相比理想反馈网络下的闭环增益，实际反馈网络的闭环增益通过修正开环增益计算可以得到：

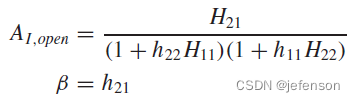
其中：

$H_{11}=\frac{V_{1}}{I_{1}}|_{V_{2}=0}$

$H_{22}=\frac{I_{2}}{V_{2}}|_{I_{1}=0}$

由于修正的开环增益符合输入输出的分压原则，通过修改原闭环电路，可以直接分析修正的开环增益，即将反馈网络同时纳入反馈输入端和反馈输出端，其中反馈输入端的反馈网络另一端需接地（ $V_{2}=0$ ），反馈输出端的反馈网络另一端需开路（ $I_{1}=0$ ），得到修正的开环电路

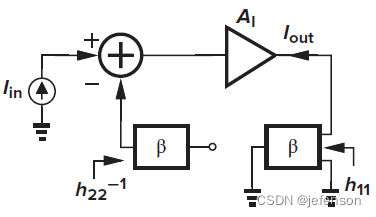
如上，对于非理想反馈网络，电流-电压放大电路的输入阻抗是修正的开环电路输入阻抗的1/(1+Aβ)，输出阻抗是修正的开环电路输出阻抗的1+Aβ倍，注意A是修正的开环增益

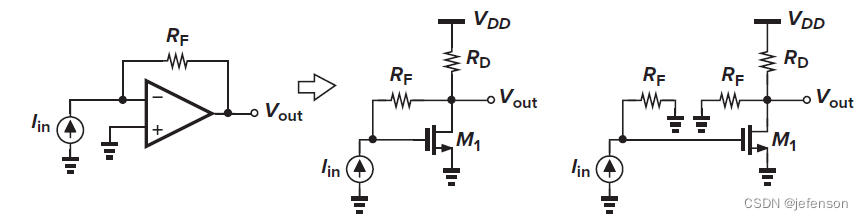
典型案例

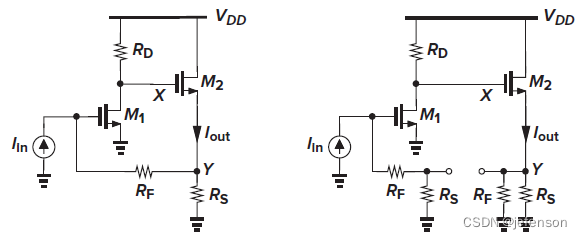
左图是典型的电流-电流负反馈放大电路，前馈网络通过反馈电阻 $R_{F}$ 、 $R_{S}$ ，以及共源极放大电路+源极跟随器实现电流放大，反馈网络通过反馈电阻 $R_{F}$ 、 $R_{S}$ 采集输出电流，负反馈逻辑：M1栅极电流上升（实际上栅极无电流，替换为三极管更易理解）→M2源极电流下降→反馈电阻 $R_{F}$ 电流上升→M1栅极电流下降。按照右图重构电路计算修正的开环增益，根据诺顿定理，M2可等效为电流源与输出阻抗并联，输出阻抗是 $1/g_{m}+R_{S}\parallel R_{F}$ ，需确保 $R_{F}\gg R_{S}$ ，避免输出阻抗下降