1. 一般统计量
均值、方差、最小值、最大值、1%分位数、5%分位数、 10%分位数、25%分位数、 50%分位数、75%分位数、90%分位数、 95%分位数、 99%分位数。
一般要将数据排序后才能求得分位数。
1.1 对每个Model(SEG_A、SEG_B、SEG_C、ALL),计算score向量的统计量
2. Pearson相关系数
其公式为:

其中:
0.8-1.0 极强相关
0.6-0.8 强相关
0.4-0.6 中等程度相关
0.2-0.4 弱相关
0.0-0.2 极弱相关或无相关
3.PSI
PSI(Population Stability Index)是衡量模型的预测值与实际值偏差大小的指标。PSI 小于 0.25 意味偏差在可以接受的范围里。

群体稳定性指标(population stability index),
公式: psi = sum((实际占比-预期占比)*ln(实际占比/预期占比))
举个例子解释下,比如训练一个logistic回归模型,预测时候会有个概率输出p。你测试集上的输出设定为p1吧,将它从小到大排序后10等分,如0-0.1,0.1-0.2,......。
现在你用这个模型去对新的样本进行预测,预测结果叫p2,按p1的区间也划分为10等分。
实际占比就是p2上在各区间的用户占比,预期占比就是p1上各区间的用户占比。
意义就是如果模型跟稳定,那么p1和p2上各区间的用户应该是相近的,占比不会变动很大,也就是预测出来的概率不会差距很大。
一般认为psi小于0.1时候模型稳定性很高,0.1-0.25一般,大于0.25模型稳定性差,建议重做。
4.VIF
方差膨胀因子(Variance Inflation Factor,VIF):容忍度的倒数,VIF越大,显示共线性越严重。经验判断方法表明:当0<VIF<10,不存在多重共线性;当10≤VIF<100,存在较强的多重共线性;当VIF≥100,存在严重多重共线性。
计算方法: 对自变量作中心标准化,则X'X 为自变量的相关阵,定义
则矩阵C的主对角线元素 VIF(i) 为自变量X(i) 的方差扩大因子VIF。 若X(i) 与其余自变量的复决定系数为R(i)^2,VIF 与 复决定系数关系为:
4.1 对每个Model的SEG_A、SEG_B、SEG_C、ALL,计算每个signal的VIF:
(1). Signal的全矩阵为X
(2). 从X取得一列signal y,从X中删除y得X'
(3). 对X',y作线性回归建模,得到模型LR
(4). 使用LR,输入X,得到y的预测值y_pred
(5). 求得y的VIF= sum((y- y_mean)^2)/sum((y- y_pred)^2)
(6).从第二步开始重复,计算每个signal的VIF
5. ROC曲线
受试者工作特征曲线 (receiver operating characteristic curve,简称ROC曲线): 是反映敏感性和特异性连续变量的综合指标,是用构图法揭示敏感性和特异性的相互关系,它通过将连续变量设定出多个不同的临界值,从而计算出一系列敏感性和特异性,再以敏感性为纵坐标、(1-特异性)为横坐标绘制成曲线,曲线下面积越大,诊断准确性越高。在ROC曲线上,最靠近坐标图左上方的点为敏感性和特异性均较高的临界值。
5.1. 对每个Model(只有SEG_A),计算score与tag的ROC曲线:
(1). 将score 降序排列
(2). score划分为10等份(每份个数相同)
(3). 计算每一份tag的总和即命中个数,score的最大、最小值
(4). 计算每一份的未命中个数 = 个数- 命中个数
(5). 转化为累加矩阵,计算累加命中率、累加未命中率
(6). 计算 KS = max ( abs (累加命中率[i] - 累加未命中率[i]) )
(7). 计算 AUROC = sum ( (累加命中率[i] + 累加命中率[i-1])*( 累加未命中率[i] - 累加未命中率[i-1]) )/2 , 即求积分
(8). 计算累加前每层实际命中率、累加前每层预测命中率、每层累加率
(9). ROC 曲线:X轴为累加未命中率[i]),y轴为累加命中率[i]。
6. AUC
Area Under the ROC Curve,ROC 曲线下的面积,AUC 值在0.5 到1 之间。
7.KS
8. CI
Condition Index 条件指数:用于诊断多重共线性。
CI > 100 | 强 多重共线性 | |
CI > 30 | 中等多重共线性 | |
CI > 10 | 弱多重共线性 |
Condition Index 条件指数 计算方法:计算矩阵X‘X 的特征值,则条件数K和条件指数CI分别为:
8.1. 对每个Model(SEG_A、SEG_B、SEG_C),计算signal的CI:
(1). 求出回归矩阵S‘S
(2).求出矩阵S‘S的特征值lam1、lam2........lamN
(3). 求最大特征值/最小特征值 的平方根
9. Logit Plot
9.1. 对每个Model(只有SEG_A),计算signal与tag的logit关系:
(1). 若signal 是标签类型,则计算其值分别为0、1时候,对应的tag的数量、均值
(2). 若signal 是数值类型,则将signal划分为最多10个区间,计算各个区间对应的tag的数量、均值
10. CRC
10.1 对每个Model(只有SEG_A),计算score与tag 之间的线性关系:
(1). 按照score降序排列
(2). 划分为10个等份,求出每一份的score和tag的均值
(3). 使用score均值和tag均值进行线性回归建立模型LR
(4). 按照模型LR,使用score均值作为变量,带入模型LR中,计算出预测的tag均值







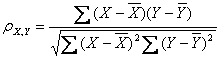
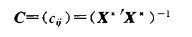
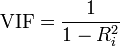















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








