瞎聊机器学习——LR（Logistic Regression）逻辑斯蒂回归（一）

最新推荐文章于 2023-05-11 16:14:58 发布

二哥不像程序员

最新推荐文章于 2023-05-11 16:14:58 发布

阅读量1.1k

点赞数 1

分类专栏：机器学习文章标签：逻辑斯蒂机器学习

本文链接：https://blog.csdn.net/qq_35164554/article/details/89431982

版权

机器学习专栏收录该内容

48 篇文章 12 订阅

订阅专栏

逻辑斯蒂回归是我们在学习以及工作中经常用到的一种分类模型，下面通过本文来讲解一下逻辑斯蒂回归（logistic regression，下文简称LR）的概念、数学推导。

一、逻辑斯蒂回归的概念

首先希望大家明确一点，虽然该算法的名字叫做逻辑斯蒂回归（我也不知道为什么这么翻译）但其实它是一种分类模型，一定不能把它和线性回归混为一谈。简单说一下分类和回归之间的区别：

分类：给定一个数据，根据给出的训练集训练模型并推断出它所对应的类别（+1，-1），是一种定性的输出，也叫作离散变量预测。

回归：给定一个数据，根据给出的训练集训练模型并推断出该数据下的输出值是多少，此时输出的是一个真实的数值，是一种定量的输出，也叫作连续变量预测。

明白了LR是一种怎样的模型，下面我们来说一下它的具体概念。

LR模型其实就是在线性回归的基础上有套用了一个逻辑函数（sigmoid），就是因为这个逻辑函数让LR成为了机器学习中的一种经典的分类方法，下文中我们会详细的讲到这个逻辑函数是什么及其使用方法。

LR是一种极易理解的模型，就相当于y=f(x)，表名自变量x和因变量y之间的关系。比如购房时我们需要考虑房子的楼层、面积、价钱、位置再去考虑买与不买，这其中楼层、面积、价钱、位置就是自变量x，即特征数据，而判断买与不买相当于获取的因变量y，即预测分类。

二、逻辑斯蒂分布

逻辑斯蒂分布也叫作增长分布，其分布函数是一个增长函数。

设X是连续随机变量，X服从逻辑斯谛分布是指X具有下列分布函数和密度函数：

分布函数： $F(x)=P(X\leqslant x)=\frac{1}{1+e^{-(x-\mu )/y}}$

密度函数： $f(x)=F'(x)=\frac{e^{-(x-\mu)/y}}{\gamma (1+e^{-(x-\mu)/y})^{2}}$

上式中， $\mu$ 为位置参数， $\gamma > 0$ 为形状参数。

在不同的参数下概率密度函数 $p(x;\mu ,\gamma )$ 的图像如下所示（图中的s是参数 $\gamma$ ）：

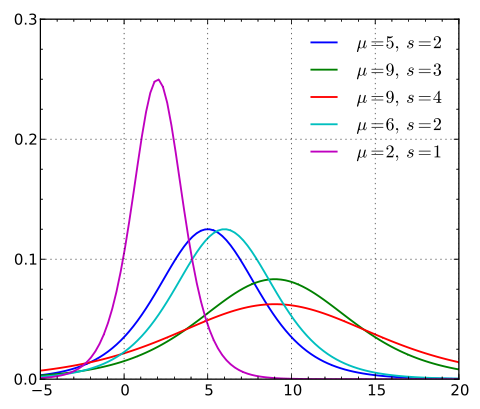
480px-Logisticpdfunction.svg.png-45.2kB

在不同参数下分布函数 $p(x;\mu ,\gamma )$ 的图像如下所示（图中的s是参数 $\gamma$ ）：

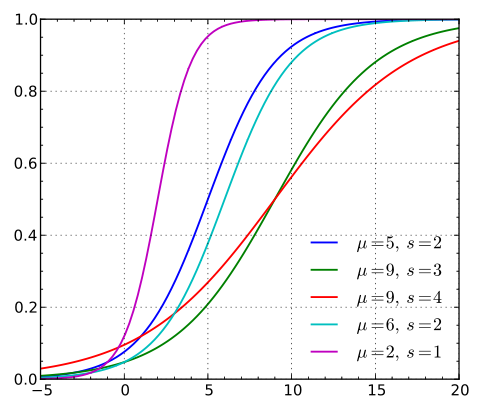
480px-Logistic_cdf.svg.png-49.9kB

根据分布函数我们可以看出图像呈s型，且关于点 $(\mu,\frac{1}{2})$ 成中心对称，曲线在两端的增长速度很慢，在中间的增长速度很快，且 $\gamma$ （s）的值越小增长速度越快。

当我们选择 $\mu=0,\gamma=1$ 的时候，逻辑斯蒂概率分布函数就是我们逻辑斯蒂回归中药用到的sigmoid函数，即：

$sigmoid(z)=g(z)=\frac{1}{1+e^{-z}}$

其导数： $g'(z)=g(z)(1-g(z))$ (这是一个很好的性质，后文中我们会用到）。

三、逻辑斯蒂回归

上一模块中我们说了逻辑斯蒂分布及其如何产生sigmoid函数，本节中我们继续研究逻辑斯蒂回归模型。

从二分类入手，给定数据集 $D({(x_{i},y_{i})}_1^{m})$ ，我们希望对于输入数据 $x\in R$ ,有输出 $y_{i}\in\left \{ 0,1 \right \}$ ，一类为正例，一类为负例。

首先我们进行一个设定（g(z)表示sigmoid函数）：

$x^\left ( i \right )$ 为正例的概率： $h_{\theta }\left(x^\left ( i \right )\right)=g\left(\theta^T x^\left ( i \right )\right)$

$x^\left ( i \right )$ 为负例的概率： $1-h_{\theta }\left(x^\left ( i \right )\right)=1-g\left(\theta^T x^\left ( i \right )\right)$

对于真实标记为正例的样本我们希望 $h_{\theta }\left(x^\left ( i \right )\right)$ 越大越好。

对于真实标记为负例的样本我们希望 $1-h_{\theta }\left(x^\left ( i \right )\right)$ 越大越好。

利用极大似然，我们希望：

$max \prod_{i=1}^{m}=h_{\theta }\left(x^\left ( i \right )\right)^{\left(y^{\left(i\right)}\right)}*(1-h_{\theta }\left(x^\left ( i \right )\right))^{\left(1-y^\left(i\right)\right) }$

即：

$max\frac{1}{m}\sum_{i=1}^{m}y^{(i)}log (h_{(\theta) }(x^{(i)}))+(1-y^{(i)})log(1- h_{(\theta) }(x^{(i)}))$

即：

$loss = -\frac{1}{m}\sum_{i=1}^{m}y^{(i)}log (h_{(\theta) }(x^{(i)}))+(1-y^{(i)})log(1- h_{(\theta) }(x^{(i)}))$

在实际应用中我们需要不断的减小loss使得模型优化，我们采用梯度下降法来优化模型：（）

（对loss进行求导，我们只处理 $\sum$ 后的补分即可）

$\frac{dl}{d\theta}=y*\frac{1}{h_{\theta}(x)}*h_{\theta}'(x)*x+(1-y)*\frac{1}{1-h_{\theta}(x)}*(-h_{\theta}'(x))*x$

$=y*(1-h_{\theta}(x))*x+(1-y)*h_{\theta}(x)*x*-1$ （此处用到sigmoid函数的求导特性）

$=(y-h_{\theta}(x))*x$

由此可得梯度为：

$grads=\sum_{i=1}^{m}(y^{(i)}-h_{\theta}(x^{(i)}))*x^{(i)}$

梯度参数更新即为：

$\theta:=\theta-\sum_{i=1}^{m}(y^{(i)}-h_{\theta}(x^{(i)}))*x^{(i)}$

以上便是逻辑斯蒂回归的损失函数的推导以及梯度下降法参数更新的推导过程，下一篇中我们会利用代码来实现逻辑斯蒂回归。

四、逻辑斯蒂回归的特点

优点：计算代价不高，易于实现和理解

缺点：容易欠拟合，分类精度可能不高

适用的数据类型：数值型和标称型数据

二哥不像程序员

关注

1
点赞
踩
6

收藏

觉得还不错? 一键收藏
打赏
0
评论
瞎聊机器学习——LR（Logistic Regression）逻辑斯蒂回归（一）

逻辑斯蒂回归是我们在学习以及工作中经常用到的一种分类模型，下面通过本文来讲解一下逻辑斯蒂回归（logistic regression，下文简称LR）的概念、数学推导。一、逻辑斯蒂回归的概念首先希望大家明确一点，虽然该算法的名字叫做逻辑斯蒂回归（我也不知道为什么这么翻译）但其实它是一种分类模型，一定不能把它和线性回归混为一谈。简单说一下分类和回归之间的区别：分类：给定一个数据，根据给出的...
复制链接

扫一扫