最短路径算法 Dijkstra算法 Floyd算法 简述

Dijkstra算法

又称迪杰斯特拉算法，是一个经典的最短路径算法，主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止，使用了广度优先搜索解决赋权有向图的单源最短路径问题，算法最终得到一个最短路径树。时间复杂度为O(N^2)

执行动画：

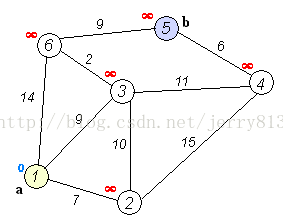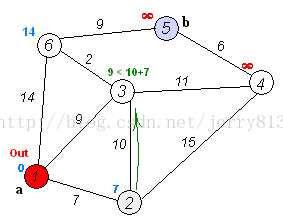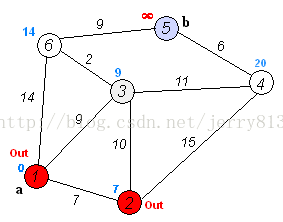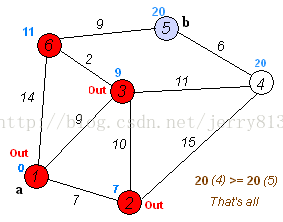
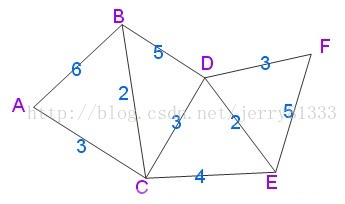
实例：

抽象步骤：

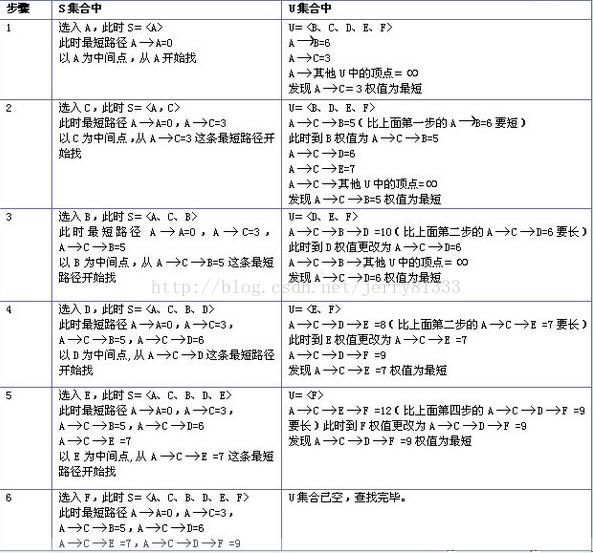
1.将起点A放入集合中，A点的权值为0,因为A->A=0。

2.与起点A相连的所有点的权值设置为A->点的距离，连接不到的设置为无穷。并且找出其中最小权值的B放入集合中（此时A->B必定为最小距离）。

3.与B点相连的所有点的权值设置为B->点的距离，并且找出其中最小权值的C点放入集合中（此时C的权值必定为其最小距离）。

4.重复步骤3，直至所有点加入集合中。便能得到所有点与A点的最短距离。

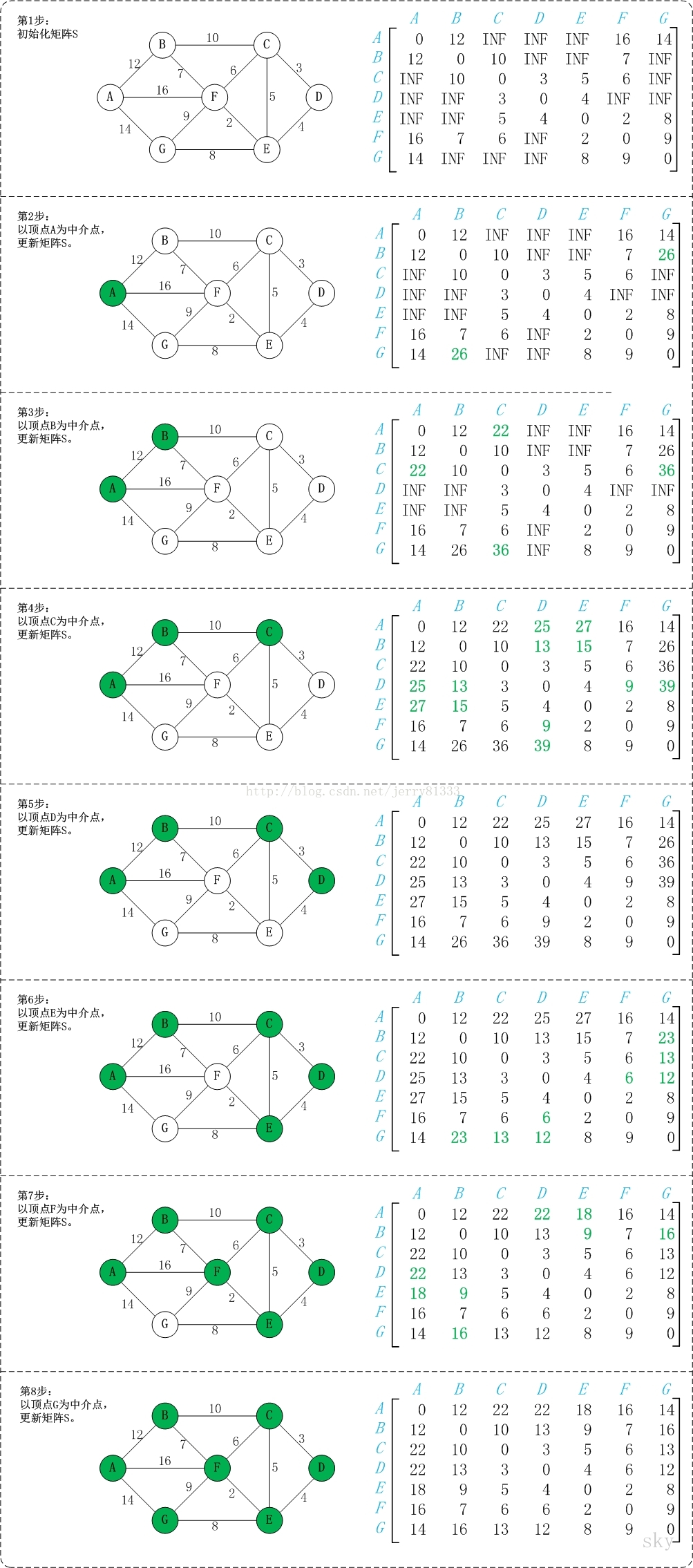
Floyd算法

全称Floyd-Warshall算法，又称佛洛依德算法，是解决任意两点间的最短路径的一种算法，但是时间复杂度比迪杰斯特拉要高，时间复杂度为O(N^3)吗，空间复杂度为O(N^2)。

简单案例：

步骤：

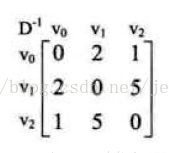
1.将图转化成矩阵：

2.选择V0点作为第一个中间点：

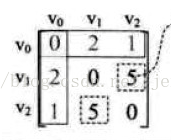
3.进行V0中间点是否能缩短另外两点间距离的判断：简而言之就是非对角线处（红箭头处）进行加法判断，<则替换。

4.对后续点进行步骤2-3相应的操作。

范例：

INF表示无穷大。