根据我浅薄的知识,以及粗浅的语言,随意总结一下。
1.曼哈顿距离
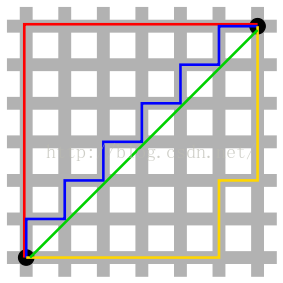
曼哈顿距离又称Manhattan distance,还见到过更加形象的,叫出租车距离的。具体贴一张图,应该就能明白。
上图摘自维基百科,红蓝黄皆为曼哈顿距离,绿色为欧式距离。
2.欧式距离
欧式距离又称欧几里得距离或欧几里得度量(Euclidean Metric),以空间为基准的两点之间最短距离,与之后的切比雪夫距离的差别是,只算在空间下。
说的通俗点,就是初中知识,两点之间直线最短的概念。
3.切比雪夫距离
切比雪夫距离又称(Chebyshev distance)或者(Supremum distance)。
这是一个最装逼的距离,因为需要使用时候,其纬度起码为3及以上。
数学上,切比雪夫距离(Chebyshev distance)或是L∞度量是向量空间中的一种度量,二个点之间的距离定义为其各座标数值差的最大值。
上句摘自维基百科,但是这玩意鬼看得懂啊,为了更好的理解切比雪夫距离,我在这里举一个通俗易懂的例子:
比如,有同样两个人,在纽约准备到北京参拜天安门,同一个地点出发的话,按照欧式距离来计算,是完全一样的。
但是按照切比雪夫距离,这是完全不同的概念了。
譬如,其中一个人是土豪,另一个人是中产阶级,第一个人就能当晚直接头等舱走人,而第二个人可能就要等机票什么时候打折再去,或者选择坐船什么的。
这样来看的话,距离是不是就不一样了呢?
或者还是不清楚,我再说的详细点。
同样是这两个人,欧式距离是直接算最短距离的,而切比雪夫距离可能还得加上财力,比如第一个人财富值100,第二个只有30,虽然物理距离一样,但是所包含的内容却是不同的。
4.明式距离
明氏距离又叫做明可夫斯基距离(Minkowski distance),根本不是种概念,或者可以说是以一种集合或者公式。
当纬度等于1时候,其公式等价于曼哈顿距离。
等于2时候,其公式等价于欧式距离。
当大于2到无穷大时候,其公式等价于切比雪夫距离。








 本文深入浅出地介绍了四种常用的距离度量方法:曼哈顿距离、欧式距离、切比雪夫距离及明可夫斯基距离,并通过实例帮助读者更好地理解它们的应用场景。
本文深入浅出地介绍了四种常用的距离度量方法:曼哈顿距离、欧式距离、切比雪夫距离及明可夫斯基距离,并通过实例帮助读者更好地理解它们的应用场景。
















 1499
1499

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








