写的不错,学习了
http://blog.csdn.net/zy825316/article/details/18625583
什么是推荐?
推荐,就是根据个人偏好,对某个人进行个性化推荐。
- 在线购物的商品推荐
- 热门网站的推荐
- 音乐推荐
- 电影、电视的推荐
通常,我们会询问朋友有什么好看的电影,当然正常人都会询问和自己有着相同爱好的人。那么有一种算法叫做协同过滤:就是找到和目标用户有着相同爱好的人,然推荐给目标用户,这些有相同爱好的人喜欢的物品。本文主要就是讲这个算法。
推荐电影的例子
用户的历史操作
#一个字典,第一个key是人名,value是又是一个字典,字典里面是key电影名,value是评分
critics={'Lisa Rose': {'Lady in the Water': 2.5, 'Snakes on a Plane': 3.5,
'Just My Luck': 3.0, 'Superman Returns': 3.5, 'You, Me and Dupree': 2.5,
'The Night Listener': 3.0},
'Gene Seymour': {'Lady in the Water': 3.0, 'Snakes on a Plane': 3.5,
'Just My Luck': 1.5, 'Superman Returns': 5.0, 'The Night Listener': 3.0,
'You, Me and Dupree': 3.5},
'Michael Phillips': {'Lady in the Water': 2.5, 'Snakes on a Plane': 3.0,
'Superman Returns': 3.5, 'The Night Listener': 4.0},
'Claudia Puig': {'Snakes on a Plane': 3.5, 'Just My Luck': 3.0,
'The Night Listener': 4.5, 'Superman Returns': 4.0,
'You, Me and Dupree': 2.5},
'Mick LaSalle': {'Lady in the Water': 3.0, 'Snakes on a Plane': 4.0,
'Just My Luck': 2.0, 'Superman Returns': 3.0, 'The Night Listener': 3.0,
'You, Me and Dupree': 2.0},
'Jack Matthews': {'Lady in the Water': 3.0, 'Snakes on a Plane': 4.0,
'The Night Listener': 3.0, 'Superman Returns': 5.0, 'You, Me and Dupree': 3.5},
'Toby': {'Snakes on a Plane':4.5,'You, Me and Dupree':1.0,'Superman Returns':4.0}}用数字来代表行为是一个非常关键的手段。这样才编程的进行运行,如下图所示:
基于用户的协同过滤
协同过滤:就是找到和目标用户有着相同爱好的人,然推荐给目标用户,这些有相同爱好的人喜欢的物品。本文主要就是讲这个算法。
计算用户相似度
那么现在我们已经有了用户数据了,下一步就是:找出爱好相同的用户。专业术语:寻找相近用户或者相似度高的用户。下面介绍三种计算相似度的体系:
- 欧几里得距离
- 皮尔逊相关度
- Tanimoto系数
欧几里得距离
实际上,欧几里得距离非常直观,对于某两部电影,所有的用户都对其有着评分,我们以一个电影为x轴、一个电影为y轴,将每个人的对两个电影的评分画在坐标系中,直接考察每对用户的直线距离,距离近的相似度高。比如电影:dupree和snake,可以画出的图如下所示:

虽然这幅图只使用了二维坐标系,但实际上三维、四维都是同样的道理。
求两点间直线的距离,我相信大家都知道怎么算吧?三维、四维、n维的其实和二维的一个道理,都是两点差的平方和,再开方。注意:两点是指两个用户。在二维中就有x,y轴两个差值的平方和,而在n维中,就是n个差值的平方和。在本题中,对于两用户,必须是共同评过分的电影才有计算的意义。求出平方和再开方就是直线距离了。现在两用户越相邻距离越小,但是我们希望得到的是用户越相邻,数值越大,(0-1之间),故我们对最后的结果加1再求倒数就可以了。试想:如果两点重合,距离为1,再求倒数则是0被除,所以必须要加一。而如果两点距离越远,求倒数后值越小,符合我们的要求。解释清楚之后,让我们来看一看代码:
from math import sqrt
#利用欧几里得计算两个人之间的相似度
def sim_distance(prefs,person1,person2):
#首先把这个两个用户共同拥有评过分电影给找出来,方法是建立一个字典,字典的key电影名字,电影的值就是1
si={}
for item in prefs[person1]:
if item in prefs[person2]:
si[item]=1
#如果亮着没有共同之处
if len(si)==0:return 0
#计算所有差值的平方和
sum_of_squares=sum([pow(prefs[person1][item]-prefs[person2][item],2) for item in prefs[person1] if item in prefs[person2]])
return 1/(1+sqrt(sum_of_squares))
print sim_distance(critics,'Lisa Rose','Claudia Puig')最后一句代码可以计算两个实例。
皮尔逊相关度评价

图中superman电影的坐标为(3.0,5.0),这是因为用户Gene Seymour对其的评分为5,而mick lasalle的评分为3.考虑所有的点:我们画一条线,叫最佳拟合线:画的原则是尽可能地靠近图中所有的坐标点。就是上图的线,试想一种情况就是两个用户的评分完成一样,我们将得到一条线:所有点都在线上,而且线的角度是45度。这时,两个用户的兴趣完全相同,我们称之为1,我想别的拟合线与之对比即可看出差距吧。
我来看一种情况较好的时候:上图的相关系数为0.4,下图为0.75
公式如下:其中X和Y分别是个数相同的数组或者是列表(python),相当于算出了两个数组之间的perason相关度。
请看代码:
#返回两个人的皮尔逊相关系数
def sim_pearson(prefs,p1,p2):
si={}
for item in prefs[p1]:
if item in prefs[p2]: si[item]=1
#得到列表元素的个数
n=len(si)
#如果两者没有共同之处,则返回0
if n==0:return 1
#对共同拥有的物品的评分,分别求和
sum1=sum([prefs[p1][it] for it in si])
sum2=sum([prefs[p2][it] for it in si])
#求平方和
sum1Sq=sum([pow(prefs[p1][it],2)for it in si])
sum2Sq=sum([pow(prefs[p2][it],2)for it in si])
#求乘积之和
pSum=sum([prefs[p1][it]*prefs[p2][it] for it in si])
#计算皮尔逊评价值
num=pSum-(sum1*sum2/n)
den=sqrt((sum1Sq-pow(sum1,2)/n)*(sum2Sq-pow(sum2,2)/n))
if den == 0:return 0
r=num/den
return r
print sim_pearson(critics,'Lisa Rose','Gene Seymour')虽然两者都可以计算出相关度,哪个更好取决于实际的应用。但是pearson有一个明显非常不错的地方,它可以忽略掉一种情况:比如A用户每次给出的分都比B用户高,也就是说A给的分普遍较高,那么此时如果用欧几里得距离的算法的话,会判定A与B的相似度比较低。然而pearson算法可以修正这一点,依然会得出A与B的相似度较高。pearson为什么会有这样的特点呢?举例即可看出,如下图所示:
我给A写了两次评分,第二次评分恰好比第一次评分少了2分。画出来的两条线确实平行的,它们与45度的线的角度差距是一样的。我暂时是这么认为的。但是实际上是不是还有待查证。
Tanimoto系数
再讲一个Tanimoto系数,也是用来计算相似度的。非常简单。如有两个集合
A=[shirt,shoes,pants,socks]
B=[shirt,shirt,shoes]
两个集合的交集,就是重叠部分,我们称之为C。就是[shirt,shoes]。
Na表示集合A的个数,Nb表示集合B的个数。Nc表示集合C的个数。
Tanimote系数公式如下:
代码:
def tanimoto(a,b):
c=[v for v in a if v in b]
return float(len(c))/(len(a)+len(b)-len(c))
对于这个应用没有实际的例子,只是叙述一下公式,为什么会突然在这里讲一下这个公式呢?这是因为我现在要做的项目就是音乐推荐,而我正在思考如何计算用户的相似度,那么就很有可能要利用到这个公式,实际上现在考虑的也比较多。我在合适的时候和写一篇关于这件事的博客。
除了上述三种计算相似度的公式,还有Jaccard系数和曼哈顿距离算法也可以用于相似度计算。
找出相似用户
既然可以计算每一对用户的相似度了,那么可以找出针对某一目标用户,与其兴趣相似的用户了。其实做的事就是做个循环,然后排个序,然后反转一下。代码如下:
def topMatches(prefs,person,n=5,similarity=sim_pearson):
scores=[(similarity(prefs,person,other),other)for other in prefs if other != person]
scores.sort()
scores.reverse()
return scores[0:n]
print topMatches(critics,'Toby',n=3)
产生推荐列表
我们确实可以得到与Toby兴趣相似的用户,然而,这并不是我们的最终目的,我们需要得到的是Toby可能喜欢的物品。根据书中的做法,如果从其相似用户中找随便挑一个没看过的电影做一个推荐的话,这太随意了。这一点非常重要,我现在觉得我音乐网站推荐系统也不能如此随意,但是我记得我后来将会该为基于物品的协同过滤,与此处的不同。先继续完成我的例子。
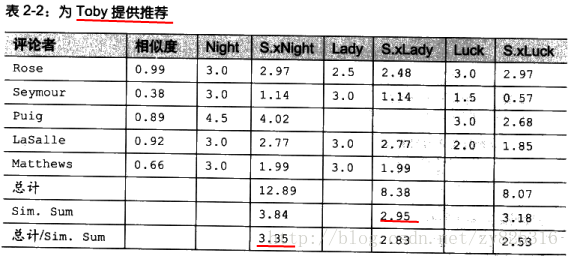
为了杜绝这样的随意,我们会采用一种利用加权的方式来为目标用户没有看过的电影的预测打分。加权的意思是指:无论与目标用户的相似度低还是高,都会影响着我们预测目标用户没看过的电影的分数,只是权重不一样而已。如下图所示
最后一排中的红线3.35即是为Toby没看过的电影Night的预测得分。具体来的就是上两排的12.89处于3.84。12.89的来历是将所有看过该电影的用户的打分乘以与toby的相似度的和。而3.84仅仅就是所有相似用户的相似度的总和。我们可以看到对于电影Lady,由于puig没有看过,所以它会对预测toby的分有任何影响。这就是说:相似度越高的用户的评分越能影响着预测目标用户对某个电影的打分。
代码如下:
#利用所有人对电影的打分,然后根据不同的人的相似度,预测目标用户对某个电影的打分
#所以函数名叫做得到推荐列表,我们当然会推荐预测分数较高的电影
#该函数写的应该是非常好,因为它我们知道的业务逻辑不太一样,但是它确实非常简单的完成任务
def getRecommendations(prefs,person,similarity=sim_pearson):
totals={}
simSums={}
for other in prefs:
#不用和自己比较了
if other==person:continue
sim=similarity(prefs,person,other)
#忽略相似度为0或者是小于0的情况
if sim<=0:continue
for item in prefs[other]:
#只对自己还没看过的电影进行评价
if item not in prefs[person] or prefs[person][item]==0:
#相似度*评价值。setdefault就是如果没有就新建,如果有,就取那个item
totals.setdefault(item,0)
totals[item]+=prefs[other][item]*sim
#相似度之和
simSums.setdefault(item,0)
simSums[item]+=sim
#建立一个归一化的列表,这哪里归一化了?这不是就是返回了一个列表吗
rankings=[(total/simSums[item],item)for item,total in totals.items()]
#返回好经过排序的列表
rankings.sort()
rankings.reverse()
return rankings
print getRecommendations(critics,'Toby')
结果:
>>>
[(3.3477895267131013, 'The Night Listener'), (2.8325499182641614, 'Lady in the Water'), (2.5309807037655645, 'Just My Luck')]
>>>
如此,一个小型的推荐系统就建立成功了。
基于物品的协同过滤
数据的转变
接下来要将一个重要的思想。就是根据利用用户对电影的评分,求出电影之间的相似度。
试想,刚刚我们在topMatches方法里面得到了什么?与用户兴趣相似的用户。现在我们要求的是与电影相似的电影。这只是需要一个思维的转变。
那就是:将用户对电影的评分看成,电影对用户的适应度。大概就是这个意思:大概电影自己给用户打了一个分:就是电影适合用户的程度。比如电影A给用户x打了4分,电影A又给用户y打了3分,结果电影B给用户x打了4分,电影B又给用户y打了3分。好吧,我们现在就说这个电影A和电影B相似度百分百。因为它们两个对用户的适应度一模一样。
这一点很有意思,我正在构思怎么用这个思路来构建我们的音乐网址的推荐系统。
使用电影的例子中,我们还是实现一下:
准备工作就是首先把字典里面的用户与电影的对应关系换一下。
转变前:
'Lisa Rose': {'Lady in the Water': 2.5, 'Snakes on a Plane': 3.5,'Just My Luck': 3.0, 'Superman Returns': 3.5, 'You, Me and Dupree': 2.5, 'The Night Listener': 3.0}
转变后:
'Lady in the Water': {'Lisa Rose': 2.5, 'Jack Matthews': 3.0, 'Michael Phillips': 2.5, 'Gene Seymour': 3.0, 'Mick LaSalle': 3.0}
转变的代码:
#将用户对电影的评分改为,电影对用户的适应度
def transformprefs(prefs):
result={}
for person in prefs:
for item in prefs[person]:
result.setdefault(item,{})
#将把用户打分,赋值给电影的适应度
result[item][person]=prefs[person][item]
return result
接着使用
print topMatches(transformprefs(critics),'Superman Returns')
我们就可以得到与'Superman Returns'相似度较高的电影
>>>
[(0.6579516949597695, 'You, Me and Dupree'), (0.4879500364742689, 'Lady in the Water'), (0.11180339887498941, 'Snakes on a Plane'), (-0.1798471947990544, 'The Night Listener'), (-0.42289003161103106, 'Just My Luck')]
>>>
甚至我们还能预测某个电影对某个用户的适应度。
代码:
print getRecommendations(transformprefs(critics),'Just My Luck')
结果:
>>>
[(4.0, 'Michael Phillips'), (3.0, 'Jack Matthews')]
>>>
注意,并不总是将人和物对调都能得到有意义的结果。对调的意义的书中一段来论述,我现在不是看的清楚,贴在这里
计算物品相似度
我们谈论的都是基于用户的协同过滤,他有一个缺点,就是当将用户与其他用户进行比较时,产生的计算时间也许会非常长。而且如果在一个物品特别多的情况下,也许会很难找出相似用户。在数据集非常多的情况,基于物品的协同过滤表现更好。
实际上这部分内容沿用了上一节,也就找出物品的相似物品。这样做有2个好处
大量计算预先进行(计算物品相似度)
给快给用户推荐的结果
由于物品的间的相似变化没那么快,所以不需要不停的为物品计算,我们只需在合适的时候计算一次就可以用很久。
让我们来看一次完整的过程,还是为Tody做一次推荐。
首先是构建相似物品集:
代码如下:
def calculateSimilarItems(prefs,n=10):
#建立相似物品的字典
result={}
#把用户对物品的评分,改为物品对用户的适应度
itemPrefs=transformprefs(prefs)
c=0
for item in itemPrefs:
c+=1
if c%100==0:print "%d / %d " %(c,len(itemPrefs))
#寻找相近的物品
scores=topMatches(itemPrefs,item,n=n,similarity=sim_distance)
result[item]=scores
return result
print calculateSimilarItems(critics)
我们可以得到结果:
>>>
{'Lady in the Water': [(0.4494897427831781, 'You, Me and Dupree'), (0.38742588672279304, 'The Night Listener'), (0.3483314773547883, 'Snakes on a Plane'), (0.3483314773547883, 'Just My Luck'), (0.2402530733520421, 'Superman Returns')], 'Snakes on a Plane': [(0.3483314773547883, 'Lady in the Water'), (0.32037724101704074, 'The Night Listener'), (0.3090169943749474, 'Superman Returns'), (0.2553967929896867, 'Just My Luck'), (0.1886378647726465, 'You, Me and Dupree')], 'Just My Luck': [(0.3483314773547883, 'Lady in the Water'), (0.32037724101704074, 'You, Me and Dupree'), (0.2989350844248255, 'The Night Listener'), (0.2553967929896867, 'Snakes on a Plane'), (0.20799159651347807, 'Superman Returns')], 'Superman Returns': [(0.3090169943749474, 'Snakes on a Plane'), (0.252650308587072, 'The Night Listener'), (0.2402530733520421, 'Lady in the Water'), (0.20799159651347807, 'Just My Luck'), (0.1918253663634734, 'You, Me and Dupree')], 'You, Me and Dupree': [(0.4494897427831781, 'Lady in the Water'), (0.32037724101704074, 'Just My Luck'), (0.29429805508554946, 'The Night Listener'), (0.1918253663634734, 'Superman Returns'), (0.1886378647726465, 'Snakes on a Plane')], 'The Night Listener': [(0.38742588672279304, 'Lady in the Water'), (0.32037724101704074, 'Snakes on a Plane'), (0.2989350844248255, 'Just My Luck'), (0.29429805508554946, 'You, Me and Dupree'), (0.252650308587072, 'Superman
Returns')]}
>>>
可以看出Lady in the water,与这部电影最想像的就是You,Me and Dupree。其他的类似。
我们为了不使得物品间的相识度变得不准确,我们会在间隔一段时间执行该函数,请记住,只有用户越多,物品间的相似度也准确。
产生推荐列表
下面是针对Toby产生一个推荐列表。实际上这个过程就在算不同的电影针对Toby的适应度的问
题。还是利用了不同电影相似度和加权的概念。如下图所示
其中,3.183是预测toby对Night电影的打分(或者电影对toby的适应度),是由1.378/0.433产生的,加了权重的分的总和,除以相似度就可以得到预测的分。本来是分的总和除以个数现在改为了加权的分的总和除以加权的个数。0.433是所有的相似度相加,1.378是由toby对不同电影打分(电影对toby的适应度)乘以相似度之后的一个数,再把对所有已经评价的电影的这个数相加。
看代码和结果:
def getRecommendedItems(prefs,itemSim,user):
userRatings=prefs[user]
scores={}
totalSim={}
#循环遍历由当前用户评分的物品
for (item,rating) in userRatings.items():
#循环遍历与当前物品相近的物品
for (similarity,item2) in itemSim[item]:
#如果该用户已经对当前物品做过评价,则将其忽略
if item2 in userRatings:continue
#打分和相似度的加权之和
scores.setdefault(item2,0)
scores[item2]+=similarity*rating
#某一电影的与其他电影的相似度之和
totalSim.setdefault(item2,0)
totalSim[item2]+=similarity
#将经过加权的评分除以相似度,求出对这一电影的评分
rankings=[(score/totalSim[item],item) for item,score in scores.items()]
#排序后转换
rankings.sort()
rankings.reverse()
return rankings
print getRecommendedItems(critics,calculateSimilarItems(critics),'Toby')
结果:
>>>
[(3.1667425234070894, 'The Night Listener'), (2.936629402844435, 'Just My Luck'), (2.868767392626467, 'Lady in the Water')]
>>>
基于用户、基于物品的选择
最后分析一下对于基于用户的协同过滤和基于物品的协同过滤的选择问题。
首先书中提到了两点:
生成推荐列表时,基于物品的方式比基于用户的方式速度更快
维护物品相似度表有着额外的开销
接着,在准确率上,又提出两点:
- 对于稀疏数据集,基于物品的方式要优于基于用户的方式
- 对于密集数据集,两者效果几乎一样
关于是什么是密集什么是稀疏,我现在的理解就是。电影与评论电影的人相比,明显电影少,人多,所以每个用户都几乎对每一个电影做了评价,这就是密集型的。而书签多,用户少,大部分书签都被少量用户收集,这就是稀疏。这里的结论我觉得很重要。
到此,整个推荐的学习,我觉得足够了,而且非常充实。
针对我的项目做的思考
我也写了一个demo,见:MyRecommendation for music。其中改变了一点代码,而且数据集改为了0和1,1代表收藏了这首歌,0代表没有。本次书中代码确实可以以一份例子为基础产生推荐列表。
如下问题值得思考
- 那么音乐到底属于稀疏还是密集呢?音乐又不像电影那么少,又不像书签那么多。其实这个问题可以不回答。
- 但是由于基于物品方式更快,所以我决定使用基于物品的方式,但是到底又有多快呢?这是我非常困惑的地方。够不够每次用户点下一曲时计算一次呢?例子中每个用户都要把每首歌。都作为字典存起来,这个数据量是非常大的,当然再经过了第三题的启示,在一次计算中应该只需要把五位相似用户和一位目标用户的歌组织成字典就可以了。
- 本书课后题3个的描述也为快速产生推荐列表提供了一个思路,那就是我们预先计算好用的相似用户,保留五位相相似用户。再从这些相似用户中选出歌曲。那么我们可以等用户不在线的时候为其产生相似用户,如果只有五位相似用户,再从五位相似用户中计算出歌曲的话,我觉得速度应该要快很多。
全部源代码
MyRecommendation.py
# -*- coding: cp936 -*-
#一个字典,第一个key是人名,value是又是一个字典,字典里面是key电影名,value是评分
critics={'Lisa Rose': {'Lady in the Water': 2.5, 'Snakes on a Plane': 3.5,
'Just My Luck': 3.0, 'Superman Returns': 3.5, 'You, Me and Dupree': 2.5,
'The Night Listener': 3.0},
'Gene Seymour': {'Lady in the Water': 3.0, 'Snakes on a Plane': 3.5,
'Just My Luck': 1.5, 'Superman Returns': 5.0, 'The Night Listener': 3.0,
'You, Me and Dupree': 3.5},
'Michael Phillips': {'Lady in the Water': 2.5, 'Snakes on a Plane': 3.0,
'Superman Returns': 3.5, 'The Night Listener': 4.0},
'Claudia Puig': {'Snakes on a Plane': 3.5, 'Just My Luck': 3.0,
'The Night Listener': 4.5, 'Superman Returns': 4.0,
'You, Me and Dupree': 2.5},
'Mick LaSalle': {'Lady in the Water': 3.0, 'Snakes on a Plane': 4.0,
'Just My Luck': 2.0, 'Superman Returns': 3.0, 'The Night Listener': 3.0,
'You, Me and Dupree': 2.0},
'Jack Matthews': {'Lady in the Water': 3.0, 'Snakes on a Plane': 4.0,
'The Night Listener': 3.0, 'Superman Returns': 5.0, 'You, Me and Dupree': 3.5},
'Toby': {'Snakes on a Plane':4.5,'You, Me and Dupree':1.0,'Superman Returns':4.0}}
from math import sqrt
#利用欧几里得计算两个人之间的相似度
def sim_distance(prefs,person1,person2):
#首先把这个两个用户共同拥有评过分电影给找出来,方法是建立一个字典,字典的key电影名字,电影的值就是1
si={}
for item in prefs[person1]:
if item in prefs[person2]:
si[item]=1
#如果亮着没有共同之处
if len(si)==0:return 0
#计算所有差值的平方和
sum_of_squares=sum([pow(prefs[person1][item]-prefs[person2][item],2) for item in prefs[person1] if item in prefs[person2]])
return 1/(1+sqrt(sum_of_squares))
#返回两个人的皮尔逊相关系数
def sim_pearson(prefs,p1,p2):
si={}
for item in prefs[p1]:
if item in prefs[p2]: si[item]=1
#得到列表元素的个数
n=len(si)
#如果两者没有共同之处,则返回0
if n==0:return 1
#对共同拥有的物品的评分,分别求和
sum1=sum([prefs[p1][it] for it in si])
sum2=sum([prefs[p2][it] for it in si])
#求平方和
sum1Sq=sum([pow(prefs[p1][it],2)for it in si])
sum2Sq=sum([pow(prefs[p2][it],2)for it in si])
#求乘积之和
pSum=sum([prefs[p1][it]*prefs[p2][it] for it in si])
#计算皮尔逊评价值
num=pSum-(sum1*sum2/n)
den=sqrt((sum1Sq-pow(sum1,2)/n)*(sum2Sq-pow(sum2,2)/n))
if den == 0:return 0
r=num/den
return r
def tanimoto(a,b):
c=[v for v in a if v in b]
return float(len(c))/(len(a)+len(b)-len(c))
#针对一个目标用户,返回和其相似度高的人
#返回的个数N和相似度的函数可以选择
def topMatches(prefs,person,n=5,similarity=sim_pearson):
scores=[(similarity(prefs,person,other),other)for other in prefs if other != person]
scores.sort()
scores.reverse()
return scores[0:n]
#利用所有人对电影的打分,然后根据不同的人的相似度,预测目标用户对某个电影的打分
#所以函数名叫做得到推荐列表,我们当然会推荐预测分数较高的电影
#该函数写的应该是非常好,因为它我们知道的业务逻辑不太一样,但是它确实非常简单的完成任务
def getRecommendations(prefs,person,similarity=sim_pearson):
totals={}
simSums={}
for other in prefs:
#不用和自己比较了
if other==person:continue
sim=similarity(prefs,person,other)
#忽略相似度为0或者是小于0的情况
if sim<=0:continue
for item in prefs[other]:
#只对自己还没看过的电影进行评价
if item not in prefs[person] or prefs[person][item]==0:
#相似度*评价值。setdefault就是如果没有就新建,如果有,就取那个item
totals.setdefault(item,0)
totals[item]+=prefs[other][item]*sim
#相似度之和
simSums.setdefault(item,0)
simSums[item]+=sim
#建立一个归一化的列表,这哪里归一化了?这不是就是返回了一个列表吗
rankings=[(total/simSums[item],item)for item,total in totals.items()]
#返回好经过排序的列表
rankings.sort()
rankings.reverse()
return rankings
#将用户对电影的评分改为,电影对用户的适应度
def transformprefs(prefs):
result={}
for person in prefs:
for item in prefs[person]:
result.setdefault(item,{})
#将把用户打分,赋值给电影的适应度
result[item][person]=prefs[person][item]
return result
def calculateSimilarItems(prefs,n=10):
#建立相似物品的字典
result={}
#把用户对物品的评分,改为物品对用户的适应度
itemPrefs=transformprefs(prefs)
c=0
for item in itemPrefs:
c+=1
if c%100==0:print "%d / %d " %(c,len(itemPrefs))
#寻找相近的物品
scores=topMatches(itemPrefs,item,n=n,similarity=sim_distance)
result[item]=scores
return result
def getRecommendedItems(prefs,itemSim,user):
userRatings=prefs[user]
scores={}
totalSim={}
#循环遍历由当前用户评分的物品
for (item,rating) in userRatings.items():
#循环遍历与当前物品相近的物品
for (similarity,item2) in itemSim[item]:
#如果该用户已经对当前物品做过评价,则将其忽略
if item2 in userRatings:continue
#打分和相似度的加权之和
scores.setdefault(item2,0)
scores[item2]+=similarity*rating
#某一电影的与其他电影的相似度之和
totalSim.setdefault(item2,0)
totalSim[item2]+=similarity
#将经过加权的评分除以相似度,求出对这一电影的评分
rankings=[(score/totalSim[item],item) for item,score in scores.items()]
#排序后转换
rankings.sort()
rankings.reverse()
return rankings
print getRecommendedItems(critics,calculateSimilarItems(critics),'Toby')
MyRecommendation for music.py
主要是基于上面的MyRecommendation改编而成。
# -*- coding: cp936 -*-
#一个字典,第一个key是人名,value是又是一个字典,字典里面是key歌曲名,value是否收藏,收藏了为1,没收藏为0
critics={'Lisa Rose': {'Lady in the Water': 0, 'Snakes on a Plane': 1,
'Just My Luck': 0, 'Superman Returns': 0, 'You, Me and Dupree': 1,
'The Night Listener': 1},
'Gene Seymour':{'Lady in the Water': 0, 'Snakes on a Plane': 1,
'Just My Luck': 1, 'Superman Returns': 0, 'You, Me and Dupree': 1,
'The Night Listener': 0},
'Michael Phillips': {'Lady in the Water': 0, 'Snakes on a Plane': 1,
'Just My Luck': 1, 'Superman Returns': 0, 'You, Me and Dupree': 1,
'The Night Listener': 0},
'Claudia Puig': {'Lady in the Water': 0, 'Snakes on a Plane': 1,
'Just My Luck': 1, 'Superman Returns': 0, 'You, Me and Dupree': 0,
'The Night Listener': 1},
'Mick LaSalle': {'Lady in the Water': 1, 'Snakes on a Plane': 0,
'Just My Luck': 1, 'Superman Returns': 1, 'You, Me and Dupree': 1,
'The Night Listener': 1},
'Jack Matthews': {'Lady in the Water': 0, 'Snakes on a Plane': 0,
'Just My Luck': 0, 'Superman Returns': 1, 'You, Me and Dupree': 1,
'The Night Listener': 1},
'Toby': {'Lady in the Water': 1, 'Snakes on a Plane': 1,
'Just My Luck': 0, 'Superman Returns': 1, 'You, Me and Dupree': 0,
'The Night Listener': 0}}
from math import sqrt
#利用欧几里得计算两个人之间的相似度
def sim_distance(prefs,person1,person2):
#首先把这个两个用户共同拥有评过分电影给找出来,方法是建立一个字典,字典的key电影名字,电影的值就是1
si={}
for item in prefs[person1]:
if item in prefs[person2]:
si[item]=1
#如果亮着没有共同之处
if len(si)==0:return 0
#计算所有差值的平方和
sum_of_squares=sum([pow(prefs[person1][item]-prefs[person2][item],2) for item in prefs[person1] if item in prefs[person2]])
return 1/(1+sqrt(sum_of_squares))
#返回两个人的皮尔逊相关系数
def sim_pearson(prefs,p1,p2):
si={}
for item in prefs[p1]:
if item in prefs[p2]: si[item]=1
#得到列表元素的个数
n=len(si)
#如果两者没有共同之处,则返回0
if n==0:return 1
#对共同拥有的物品的评分,分别求和
sum1=sum([prefs[p1][it] for it in si])
sum2=sum([prefs[p2][it] for it in si])
#求平方和
sum1Sq=sum([pow(prefs[p1][it],2)for it in si])
sum2Sq=sum([pow(prefs[p2][it],2)for it in si])
#求乘积之和
pSum=sum([prefs[p1][it]*prefs[p2][it] for it in si])
#计算皮尔逊评价值
num=pSum-(sum1*sum2/n)
den=sqrt((sum1Sq-pow(sum1,2)/n)*(sum2Sq-pow(sum2,2)/n))
if den == 0:return 0
r=num/den
return r
def tanimoto(a,b):
c=[v for v in a if v in b]
return float(len(c))/(len(a)+len(b)-len(c))
#针对一个目标用户,返回和其相似度高的人
#返回的个数N和相似度的函数可以选择
def topMatches(prefs,person,n=5,similarity=sim_pearson):
scores=[(similarity(prefs,person,other),other)for other in prefs if other != person]
scores.sort()
scores.reverse()
return scores[0:n]
#利用所有人对电影的打分,然后根据不同的人的相似度,预测目标用户对某个电影的打分
#所以函数名叫做得到推荐列表,我们当然会推荐预测分数较高的电影
#该函数写的应该是非常好,因为它我们知道的业务逻辑不太一样,但是它确实非常简单的完成任务
def getRecommendations(prefs,person,similarity=sim_pearson):
totals={}
simSums={}
for other in prefs:
#不用和自己比较了
if other==person:continue
sim=similarity(prefs,person,other)
#忽略相似度为0或者是小于0的情况
if sim<=0:continue
for item in prefs[other]:
#只对自己还没看过的电影进行评价
if item not in prefs[person] or prefs[person][item]==0:
#相似度*评价值。setdefault就是如果没有就新建,如果有,就取那个item
totals.setdefault(item,0)
totals[item]+=prefs[other][item]*sim
#相似度之和
simSums.setdefault(item,0)
simSums[item]+=sim
#建立一个归一化的列表,这哪里归一化了?这不是就是返回了一个列表吗
rankings=[(total/simSums[item],item)for item,total in totals.items()]
#返回好经过排序的列表
rankings.sort()
rankings.reverse()
return rankings
#将用户对电影的评分改为,电影对用户的适应度
def transformprefs(prefs):
result={}
for person in prefs:
for item in prefs[person]:
result.setdefault(item,{})
#将把用户打分,赋值给电影的适应度
result[item][person]=prefs[person][item]
return result
def calculateSimilarItems(prefs,n=10):
#建立相似物品的字典
result={}
#把用户对物品的评分,改为物品对用户的适应度
itemPrefs=transformprefs(prefs)
c=0
for item in itemPrefs:
c+=1
if c%100==0:print "%d / %d " %(c,len(itemPrefs))
#寻找相近的物品
scores=topMatches(itemPrefs,item,n=n,similarity=sim_distance)
result[item]=scores
return result
def getRecommendedItems(prefs,itemSim,user):
userRatings=prefs[user]
scores={}
totalSim={}
#循环遍历由当前用户评分的物品
for (item,rating) in userRatings.items():
#循环遍历与当前物品相近的物品
for (similarity,item2) in itemSim[item]:
#如果该用户已经对当前物品已经收藏,则将其忽略
if prefs[user][item2]==1:continue
#打分和相似度的加权之和
scores.setdefault(item2,0)
scores[item2]+=similarity*rating
#某一电影的与其他电影的相似度之和
totalSim.setdefault(item2,0)
totalSim[item2]+=similarity
#将经过加权的评分除以相似度,求出对这一电影的评分
rankings=[(score/totalSim[item],item) for item,score in scores.items()]
#排序后转换
rankings.sort()
rankings.reverse()
return rankings
#print calculateSimilarItems(critics)
print getRecommendedItems(critics,calculateSimilarItems(critics),'Toby')
#print sim_pearson(critics,'Lisa Rose','Gene Seymour')
代码已上传网盘:
- MyRecommendation for music.py
- MyRecommendation.py









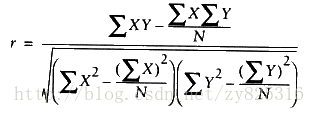

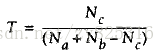















 1110
1110

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








