以下是一个实现指定范围奇数阶方阵顺时针、逆时针旋转的 Python 函数：
```python
def rotate_matrix(matrix, direction, top, bottom, left, right):
"""
旋转二维方阵中指定范围的部分，返回旋转后的方阵
:param matrix: 二维方阵
:param direction: 旋转方向，可选值为 'clockwise' 和 'counterclockwise'
:param top: 范围上边界，从 0 开始计数
:param bottom: 范围下边界，从 0 开始计数
:param left: 范围左边界，从 0 开始计数
:param right: 范围右边界，从 0 开始计数
:return: 旋转后的二维方阵
"""
# 检查输入参数是否合法
if direction not in ['clockwise', 'counterclockwise']:
raise ValueError('Invalid direction')
if top > bottom or left > right:
raise ValueError('Invalid range')
n = len(matrix)
if bottom >= n or right >= n:
raise ValueError('Range out of matrix')
# 计算方阵的中心点坐标和半径
center = (top + bottom) // 2, (left + right) // 2
radius = (bottom - top) // 2
# 根据旋转方向确定旋转角度
if direction == 'clockwise':
angle = 90
else:
angle = -90
# 逐个旋转方阵中的元素
for i in range(top, bottom+1):
for j in range(left, right+1):
# 检查当前元素是否在旋转范围内
if (i - center[0])**2 + (j - center[1])**2 <= radius**2:
# 计算旋转后的坐标
new_i = center[0] + round((i - center[0]) * math.cos(angle*math.pi/180) - (j - center[1]) * math.sin(angle*math.pi/180))
new_j = center[1] + round((i - center[0]) * math.sin(angle*math.pi/180) + (j - center[1]) * math.cos(angle*math.pi/180))
# 交换元素位置
matrix[i][j], matrix[new_i][new_j] = matrix[new_i][new_j], matrix[i][j]
return matrix
```
这个函数接受一个二维方阵 `matrix`，旋转方向 `direction`，以及一个范围 `(top, bottom, left, right)`，表示要旋转的部分的上下左右边界。函数会先根据范围计算出方阵的中心点坐标和半径，然后根据旋转方向计算旋转角度，逐个旋转范围内的元素。最后返回旋转后的方阵。
以下是一个使用示例：
```python
import math
# 创建一个 5x5 的二维方阵
matrix = [[1, 2, 3, 4, 5],
[6, 7, 8, 9, 10],
[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25]]
# 顺时针旋转范围为 (1, 3, 1, 3) 的部分
result = rotate_matrix(matrix, 'clockwise', 1, 3, 1, 3)
for row in result:
print(row)
# 逆时针旋转范围为 (1, 3, 1, 3) 的部分
result = rotate_matrix(matrix, 'counterclockwise', 1, 3, 1, 3)
for row in result:
print(row)
```
这个示例会先创建一个 5x5 的二维方阵，然后分别对范围为 (1, 3, 1, 3) 的部分进行顺时针和逆时针旋转，最后打印旋转后的结果。由于旋转部分是 3x3 的方阵，因此结果应该是：
```
[1, 2, 3, 4, 5]
[6, 13, 8, 2, 10]
[11, 9, 7, 12, 15]
[16, 14, 18, 19, 20]
[21, 22, 23, 24, 25]
[1, 2, 3, 4, 5]
[6, 7, 15, 9, 10]
[11, 13, 8, 14, 12]
[16, 17, 18, 19, 20]
[21, 22, 23, 24, 25]
```
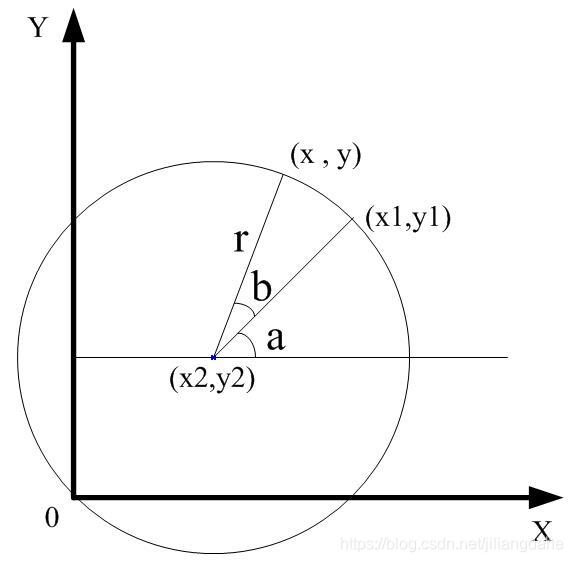
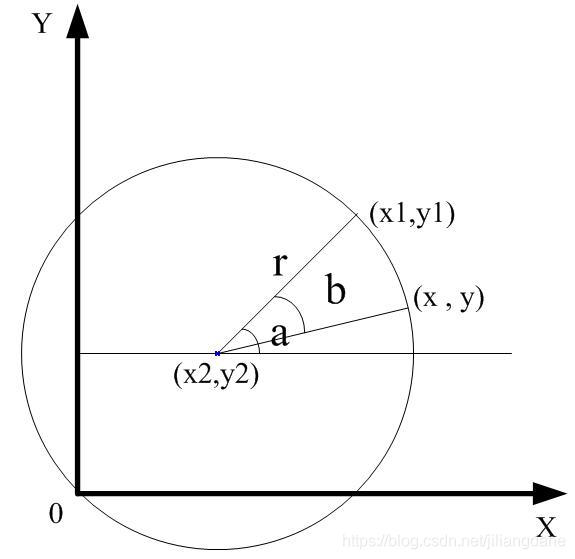
这篇博客介绍了如何在二维平面直角坐标系中，计算一点绕另一点逆时针和顺时针旋转一定角度后的新坐标。提供了详细的坐标变换公式，并给出了参考资料链接。
最低0.47元/天 解锁文章
扫一扫
1952
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
