一个点绕另一个点旋转之后的坐标计算

<(￣︶￣)Okay.

已于 2023-01-28 18:05:38 修改

阅读量2.4k

点赞数 1

分类专栏：几何编程文章标签：算法

于 2023-01-28 18:02:21 首次发布

本文链接：https://blog.csdn.net/weixin_42097108/article/details/128780588

版权

几何编程专栏收录该内容

9 篇文章

订阅专栏

本文介绍了一种基于极坐标原理的点绕指定中心旋转的数学计算方法，并提供了具体的坐标转换公式及实现代码。通过该方法可以方便地计算出点绕原点旋转后的坐标位置。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

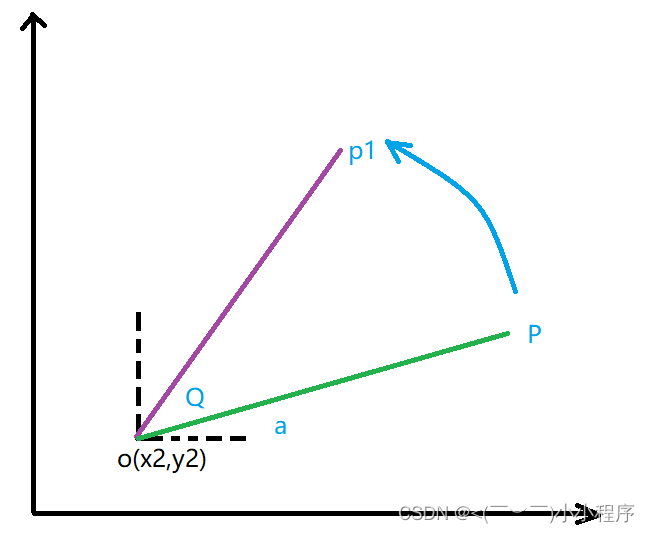
在这里插入图片描述
p点绕原点旋转角度Q，求p1坐标；
采用极坐标的方法求解
对于p点：
x = r * cos（a）；
y = r * sin（a）；
对于p1点：
x1 = r * cos（a+Q）= r * [cosacosQ - sinasinQ] = xcosQ - ysinQ；
y1 = r * sin（a+Q） = r * [sinacosQ + sinQcosa] = ycosQ + xsinQ；

在这里插入图片描述
x1 = r * cos（a+Q）= r * [cosacosQ - sinasinQ] = xcosQ - ysinQ + x2；
y1 = r * sin（a+Q） = r * [sinacosQ + sinQcosa] = ycosQ + xsinQ + y2；

// 返回点p以点o为圆心逆时针旋转alpha(单位：弧度)后所在的位置 
POINT rotate(POINT o,double alpha,POINT p) 
{ 
	POINT tp; 
	p.x-=o.x; 
	p.y-=o.y; 
	tp.x=p.x*cos(alpha)-p.y*sin(alpha)+o.x; 
	tp.y=p.y*cos(alpha)+p.x*sin(alpha)+o.y; 
	return tp; 
}