1.[10]正文中展示了可以利用替换记号,通过置t m,m
m,m n,n
n,n t,交换变量m和n的值。请说明怎样通过一连串替换,把四个变量(a,b,c,d)重新排列成(b,c,d,a)。换句话说,a的新值是b的初始值,以此类推。试用最少的替换次数实现。
t,交换变量m和n的值。请说明怎样通过一连串替换,把四个变量(a,b,c,d)重新排列成(b,c,d,a)。换句话说,a的新值是b的初始值,以此类推。试用最少的替换次数实现。
解:除了a,b,c,d 4个变量外,新增一个变量t,通过这5个变量进行连续替换,过程如下:
ta,a
b,b
c,c
d,d
t。
public class ExchangeVariables {
public static void main(String[] args){
int[] b = new int[]{1,2,3,4};
int t = b[0];
for (int i = 0; i < b.length; i++) {
if((i+1)<b.length){
b[i] = b[i+1];
}
}
b[b.length-1]=t;
System.out.println(Arrays.toString(b));
}
}最少4次替换实现。
2.[15]证明从步骤E1第二次执行起,每次该步开始时,m必然大于n(第一次执行时可能不满足)。
解:在第一次执行步骤E1后,变量m和n的值分别是n和r原来的值,且n>r。
public class GreatestCommonFactor {
public static void main(String[] args){
int m = 119;
int n = 544;
int t = 0;
if(m<n){
t=m;
m=n;
n=t;
}
algorithmE(m,n);
}
static int algorithmE(int m,int n){
if(m%n==0){
System.out.println("最大公约数是:"+n);
return n;
}else{
if(m%n > 0){
int r=(m%n);
m=n;
n=r;
return algorithmE(m,n);
}
}
return 0;
}
}
3.[20](为了提高效率)修改算法E,使其避免出现m n之类的平凡替换操作。按照算法E的风格写出这个新算法,将其称为算法F。
n之类的平凡替换操作。按照算法E的风格写出这个新算法,将其称为算法F。
解:算法F(欧几里得算法)。给定两个正整数m和n,求它们的最大公因数。
F1.[求m/n的余数。]用n除m,令m为余数。
F2.[余数是否为0?]如果m=0,算法终止,n是答案。
F3.[求n/m的余数。]用m除n,令n为余数。
F4.[余数是否为0?]如果n=0,算法终止,m是答案;否则,返回步骤F1。 I
public class GreatestCommonFactor {
public static void main(String[] args){
int m = 119;
int n = 544;
int t = 0;
if(m<n){
t=m;
m=n;
n=t;
}
algorithmF(m,n);
}
static int algorithmF(int m,int n){
if(m%n==0){
System.out.println("最大公约数是:"+n);
return n;
}else{
m=(m%n);
if(m == 0){
return n;
}else{
n = n%m;
if(n == 0){
return m;
}else{
algorithmF(m,n);
}
}
}
return 0;
}
}
4.[16]2166与6099的最大公因数是多少?
解:有算法E,n=6099,2166,1767,399,171,57。答案是57。
public class GreatestCommonFactor {
public static void main(String[] args){
int m = 2166;
int n = 6099;
int t = 0;
if(m<n){
t=m;
m=n;
n=t;
}
algorithmE(m,n);
}
static int algorithmE(int m,int n){
if(m%n==0){
System.out.println("最大公约数是:"+n);
return n;
}else{
if(m%n > 0){
int r=(m%n);
m=n;
n=r;
return algorithmE(m,n);
}
}
return 0;
}
}
5.[12]说明“阅读本套书的步骤”其实不是一个真正的算法,因为在算法的五个特征中,它至少缺少三个!另外请指出它与算法E在格式上的差异。
解:它不满足有限性、确定性和可行性,可能没有输出。就格式而言,在操作步号码之前没有字母,未出现概述性短语,而且没有“I”。
6.[20]当n=5时,执行算法E步骤E1的平均次数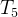 是多少?
是多少?
解:用n=5和m=1,2,3,4,5实验算法E,步骤E1执行的次数分别为2,3,4,3,1。所以步骤E1执行的平均次数是2.6=。
7.[M21] m已知,n在所有正整数范围内取值,令 为算法E中步骤E1执行的平均次数。说明
为算法E中步骤E1执行的平均次数。说明 具有合理定义。
具有合理定义。 与
与 有关系吗?
有关系吗?
解:除了数目有限的特例以外,n>m总成立。当n>m时,算法E的第1次迭代仅仅交换这两个数,所以=
+1。例如m=5,n=1,2,...,1,2,3,2,1,3,4,5,4,2,3,4,5,4,2,...的平均次数是3.6。
8.[M25]通过指定式(3)中的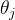 ,
, ,
,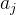 ,
,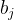 ,给出计算正整数m和n的最大公因数的“可行的”形式算法。令输入由字符串
,给出计算正整数m和n的最大公因数的“可行的”形式算法。令输入由字符串 表示,也就是在m个a后连着n个b。你的解法应当力求尽可能简单。[提示:利用算法E,把步骤E1中的除法改为置
表示,也就是在m个a后连着n个b。你的解法应当力求尽可能简单。[提示:利用算法E,把步骤E1中的除法改为置 ]
]
解:令A={a,b,c},N=5,算法结束时得到字符串
0 ab (空) 1 2 消除一个a和一个b,或者转到2.
1 (空) c 0 0 在最左端加c,转回0.
2 a b 2 3 把所有a变成b.
3 c a 3 4 把所有c变成a.
4 b b 0 5 如果还有b,重复.
每次迭代要么减少m,要么保持m不变并减少n。
9.[M30]假定 和
和 是两个计算方法。例如
是两个计算方法。例如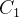 可以代表式(2)中的算法E,不过要限制m和n的大小;而
可以代表式(2)中的算法E,不过要限制m和n的大小;而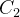 可以代表算法E的一个计算机程序实现。(因此
可以代表算法E的一个计算机程序实现。(因此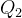 可以是计算机所以状态的集合,也就是计算机内存和寄存器所以可能得配置;
可以是计算机所以状态的集合,也就是计算机内存和寄存器所以可能得配置;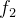 可以是计算机单步操作的定义;
可以是计算机单步操作的定义;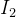 可以是初始状态的集合,包括确定最大公因数的相应程序以及m和n的值。)
可以是初始状态的集合,包括确定最大公因数的相应程序以及m和n的值。)
试就“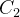 是
是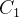 的一个表示”或者“
的一个表示”或者“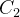 模拟
模拟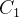 ”的概念,给出集合论定义。直观上,这就意味着
”的概念,给出集合论定义。直观上,这就意味着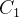 的任何计算序列都由
的任何计算序列都由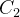 模拟实现,不过
模拟实现,不过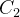 可能要用更多的计算步骤,保留更多的状态信息。(因此,我们得以严格解释“程序X是算法Y的一个实现”这一陈述。)
可能要用更多的计算步骤,保留更多的状态信息。(因此,我们得以严格解释“程序X是算法Y的一个实现”这一陈述。)
解:例如,我们说表示
,如果存在一个从
到
的函数g,一个从
到
的函数h,以及一个从
到正整数集的函数j,满足下列条件:
(a)如果x在中,那么
.
(b)如果q在中,那么
,其中
是指函数
迭代
次。
(c)如果q在中,那么
在
中的充分必要条件为q在
中。
例如,令按式(2)定义,令
有
,
,
。令
;
;
;
,如果r=0,其他情形为
;
;
;
。
现在令;
;
;
;
;
;
;
,其他情形为
。于是
表示
。
注记:读者可能希望寻找更简单的定义方式,例如令是从
到
的函数,并且仅要求当
是
中的计算序列时,
是
中以
为首项的计算序列的子序列。然而这是不恰当的。在上面的例子中,
忽略m和n的原值,但是
未忽略。
如果通过函数
表示
,而且
通过函数
表示
,那么
通过函数
表示
,其中
并且如果且
那么
因此上面定义的关系是传递的。如果函数是有界的,我们可以说
直接表示
,这个关系也是传递的。关系“
表示
”产生一个等价关系,两个计算方法等价显示当且仅当它们计算的函数是同构的;关系“
直接表示
”产生一个更有趣的等价关系,它大概相当于二者“本质上是同一个算法”的直观概念。
关于模拟的另一种定义方法,参阅罗伯特弗洛伊德和理查德
贝尔格的《机器的语言》的3.3节[The Language of Machines(Computer Science Press,1994)]。























 336
336

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










