计算机程序设计艺术卷1:基本算法 1.2.1习题

jinyongbomatt2008

已于 2024-07-28 02:12:03 修改

阅读量142

点赞数 4

分类专栏：基本算法文章标签：算法

于 2024-07-17 00:24:55 首次发布

本文链接：https://blog.csdn.net/jinyongbomatt2008/article/details/140480411

版权

基本算法专栏收录该内容

4 篇文章 0 订阅

订阅专栏

1.[05]如果要对所有非负整数n=0,1,2,...而不是对n=1,2,3,...证明某个命题P(n)，请说明应如何修改数学归纳法证明思路。

解：（a）证明P(0). （b）证明对于所有n $\geqslant$ 0,P(0),...,P(n)蕴含P(n+1)。

2.[15]下面的定理证明必定有错。错在哪里？

定理. 令a为任意整数。对于所有正整数n，有 $a^{n-1}=1$ 。

证明.如果n=1，那么 $a^{n-1}=a^{1-1}=a^{0}=1$ 。于是，按照归纳法，假设定理对1,2,...,n为真，我们有

$a^{(n+1)-1}=a^{n}=\frac{a^{n-1}\times a^{n-1}}{a^{(n-1)-1}}=\frac{1\times 1}{1}=1$ .

所以定理对n+1也为真。

解：对于n=2,定理并未证明。在证明的第二部分，取n=1,可见式中假定 $a^{(n-1)-1}=a^{-1}=1$ 。如果这个条件满足（即a=1），那么定理确实成立。

3.[18]下面定理的归纳法证明表面上是正确的，但是由于某种原因，当n=6时，等式左端给出 $\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+\frac{1}{30}=\frac{5}{8}$ ，而右端给出 $\frac{3}{2}-\frac{1}{6}=\frac{4}{3}$ 。你能找出错误吗？

定理.

$\frac{1}{1\times 2}+\frac{1}{2\times 3}+\cdots +\frac{1}{(n-1)\times n}=\frac{3}{2}-\frac{1}{n}.$

证明。我们对n用归纳法。对应n=1，显然 $3/2-1/n=1/(1\times 2).$ 假设定理对于n为真，那么 $\frac{1}{1\times 2}+\cdots +\frac{1}{(n-1)\times n}+\frac{1}{n\times (n+1)}=$ $\frac{3}{2}-\frac{1}{n}+\frac{1}{n(n+1)}=\frac{3}{2}-\frac{1}{n}+(\frac{1}{n}-\frac{1}{n+1})=\frac{3}{2}-\frac{1}{n+1}$

解：正确答案是1-2/n，错误出现在对n=1的证明中，这时公式的左端或者视为无意义，或者视为0（因为共有n-1项）。

4.[20]证明：斐波那契数除满足等式（3）外，还对一切正整数n满足 $F_{n}\geq \phi ^{n-2}.$

解：

5.[21]素数是>1且除1和其自身外没有其他正整数因数的整数。根据此定义和数学归纳法，证明每个>1的整数可以写成一个或多个素数的乘积。（一个素数视为单个素数的“乘积”，也就是它本身。）

解：如果n是素数，它显然是素数的乘积，结论是平凡的。否则，n有因数，于是存在k和m使得n=km，其中1<k,m<n。由于k和m都小于n，根据归纳法，它们可以写成素数的乘积。因此n可以写成出现在k和m的表示中的素数的乘积。

6.[20]证明：如果式（6）在步骤E4之前成立，那么在执行E4后成立。

解：用图4中的记号，我们证明A5蕴涵A6。这是显然的，因为A5蕴涵 $(a^{'}-qa)m+(b^{'}-qb)n=(a^{'}m+b^{'}n)-q(am+bm)=c-qb=r$ 。

7.[23]对于 $1^{2},2^{2}-1^{2},3^{2}-2^{2}+1^{2},4^{2}-3^{2}+2^{2}-1^{2},5^{2}-4^{2}+3^{2}-2^{2}+1^{2}$ 等和式，给出求和规则，并用归纳法予以证明。

解： $n^{2}-(n-1)^{2}+\cdots -(-1)^{n}1^{2}=1+2+\cdots +n=n(n+1)/2$ 。

8.[25]（a）用数学归纳法，证明尼科马彻斯（约公元100年）提出的下述定理： $1^{3}=1,2^{3}=3+5,3^{3}=7+9+11,4^{3}=13+15+17+19,\cdots .$ （b）利用这个结果，证明注明的公式 $1^{3}+2^{3}+\cdots +n^{3}=(1+2+\cdots +n)^{2}$ .

[注记：这公式有一个引人注目的几何解释，有沃伦勒什给出，如图5所示，见Math.Gazette 49(1965),200.其思想同尼科马彻斯定理和图3有关。在马丁加德纳的《打结的甜甜圈》（Knotted Doughnuts,New York:Freeman,1986 ）第16章以及约翰康威和理查德盖伊的《数字之篇》（The Book of Numbers,New York:Copernicus,1996）第2章中，可以找出其他“无字”证明。]

边长 $=5+5+5+5+5+5=5\cdot (5+1)$

边长 $=5+4+3+2+1+1+2+3+4+5=2\cdot (1+2+\cdots +5)$

面积 $=4\cdot 1^{2}+4\cdot 2\cdot2^{2}+4\cdot3\cdot3^{2}+4\cdot4\cdot4^{2}+4\cdot5\cdot5^{2}=4\cdot(1^{3}+2^{3}+\cdots +5^{3})$

图5 习题8(b)的几何形式

解：（a）我们证明 $(n^{2}-n+1)+(n^{2}-n+3)+\cdots +(n^{2}+n-1)$ 等于 $n^{3}$ 。事实上，由等式（2），这个和是 $n(n^{2}-n)+(1+3+\cdots +(2n-1))=n^{3}-n^{2}+n^{2}$ 。不过题目要求用归纳法证明，所以需要采用另外一种方法！对应n=1，结果是显然的。令 $n\geq 1$ ，有 $(n+1)^{2}-(n+1)=n^{2}-n+2n$ ，所以对于n+1的式子的前面各项分别比对于n的各项大2n。因此，对于n+1的和等于对于n的和加上

$\underset{n}{\underbrace{2n+\cdots +2n}}+(n+1)^{2}+(n+1)-1$ ,

这等于 $n^{3}+2n^{2}+3n+1=(n+1)^{3}$ 。（b）对于 $(n+1)^{3}$ 的第一项比对于 $n^{3}$ 的最后一项大2。所以由等式（2）， $1^{3}+2^{3}+\cdots +n^{3}=$ 从1开始的连续奇数之和= $($ 项数 $)^{2}$ $=(1+2+\cdots +n)^{2}$ 。

9.[20] 用归纳法证明：如果 $0<a<1$ ，那么 $(1-a)^{n}\geq 1-na$ 。

解：

10.[M22] 用归纳法证明：如果 $n\geq 10$ ，那么 $2^{n}\geq n^{3}$ 。

解：对于n=10是显然的。如果 $n\geq 10$ ，有 $2^n+1=2\cdot 2^{n}>(1+1/n)^{3}2^{n}$ ，根据归纳法，这大于 $(1+1/n)^{3}n^{3}=(n+1)^{3}$ 。

11.[M30]试求下式的简单求和公式，并予以证明：

$\frac{1^{3}}{1^{4}+4}-\frac{3^{3}}{3^{4}+4}+\frac{5^{3}}{5^{4}+4}-\cdots +\frac{(-1)^{n}(2n+1)^{3}}{(2n+1)^{4}+4}$

解： $(-1)^{n}(n+1)/(4(n+1)^{2}+1)$ 。

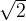12.[M25] 正文提到，可以推广算法E，使之能够接受形如 $u+v\sqrt{2}$ 的输入值，其中u和v为整数。说明如何推广，使得计算仍然可以用初等方法完成（即不用 $\sqrt{2}$ 的无穷十进制展开式）。另外证明，如果m=1和n= 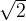$\sqrt{2}$ ，则计算不会终止。

解：这个推广唯一的不平凡之处是E2中整数q的计算。可以反复做减法，把问题归纳为判断 $u+v\sqrt{2}$ 是整数或负数还是为零，而这是容易解决的。

不难证明，当 $u+v\sqrt{2}=u^{'}+v^{'}\sqrt{2}$ 时，必有 $u=u^{'}$ 和 $v=v^{'}$ ，因为 $\sqrt{2}$ 是无理数。如果我们定义 $u+v\sqrt{2}$ 为 $a(u+v\sqrt{2})$ 的因数，当且仅当a为整数，那么1与 $\sqrt{2}$ 显然没有公因数。用这种方式扩充的算法以正规连分数计算两个输入之比，参阅4.5.3节。

[注记：然而，如果我们推广因数的概念，定义 $u+v\sqrt{2}$ 为 $a(u+v\sqrt{2})$ 的因数，当且仅当a形如 $u^{'}+v^{'}\sqrt{2}$ ，其中 $u^{'}$ 和 $v^{'}$ 是整数，那么存在一种推广算法E的方法，使得它总会终止：如果在步骤E2有 $c=u+v\sqrt{2}$ 和 $d=u^{'}+v^{'}\sqrt{2}$ ,计算 $c/d=c(u^{'}-v^{'}\sqrt{2})/(u^{'2}-2v^{'}2)=x+y\sqrt{2}$ ，其中x和y是有理数；现在令 $q=u^{''}+v^{''}\sqrt{2}$ ，其中 $u^{''}+v^{''}\sqrt{2}$ ，其中 $u^{''}$ 和 $v^{''}$ 是最接近x和y的整数，并且令 $r=c-qd$ 。如果 $r=u^{'''}+v^{'''}\sqrt{2}$ ，由此推出 $\left |u^{'''2}-2v^{'''2} \right |<\left | u^{'2}-2v^{'2} \right |$ ，因此计算将会终止。关于进一步的资料，请参阅数论教科书中的“二次欧几里得整环”部分。]

13.[M23] 扩充算法E，添加新变量T，在每一步的开头增加操作 $T\leftarrow T+1$ 。（因此，T相当于统计执行步数的计数器。）假定T的初值为0，则图4中的断言A1变为“m>0,n>0,T=0”。同样，应该把附加条件T=1添加到A2。请说明如何把附加条件添加到各个断言中，使得A1，A2，...，A6中的任何一个断言都蕴含 $T\leqslant 3n$ ，而且仍然可以实现归纳法证明。（因此，计算至多在3n步必定终止。）

解：把“ $T\leq 3(n-d)+k$ ”加进断言A3，A4，A5，A6，其中k分别取值2,3,3,1。另外把“d>0”加进断言A4。

14.[50] （弗洛伊德）编写一个计算机程序，它接受的输入是某种程序设计语言以及可选的断言。为了证明这个计算机程序是正确的，它试图补充所需的其他断言。[假如，力求编写一个程序，它能在只给定A1、A4和A6的条件下，证明算法E是正确的。关于该问题的进一步讨论，见罗伯特弗洛伊德和詹姆斯金发表在国际信息处理联合国大会会刊（IFIP Congress proceedings,1971）上的论文。]

解：

15.[HM28] （广义归纳法）正文说明了如何证明依赖于单个整数n的命题P(n)，但是没有描述如何证明依赖于两个整数m和n的命题P(m,n)。在后面这种情况，证明通常是通过某种“二重归纳法”给出的，这种归纳法常常显得不易理解。实际上，有一个比简单归纳法更一般的重要原理，它不仅适用于两个整数的情况，还适用于证明关于不可数集合的命题，例如对于所有实数x的命题P(x)。这个一般原理称为良序（well-ordering）原理。

令 $\prec$ 是集合S上的一个关系，它具备下述性质：

（i）给定S中的元素想x,y,z,如果x $\prec$ y且y $\prec$ z，那么x $\prec$ z；

（ii）给定S中的元素x和y，下面三种可能性中恰有一种为真：x $\prec$ y，x=y，y $\prec$ x；

（iii）如果A是S的任意非空子集，那么A中存在元素x，对于A中的所有元素y，满足x $\prec$ y（即x $\prec$ y或x=y）。

这个关系称为S的一个良序关系。例如，按照平常的“小于”关系<，正整数显然是良序的。

（a）证明：按照<关系，所有整数的集合不是良序。

（b）在所有整数的集合上定义一个良序关系。

（c）按照<关系，所有非负整数的集合是良序的吗？

（d）（字典序）令S按 $\prec$ 关系是良序的；对于n>0,令 $T_{n}$ 为S中的元素 $x_{j}$ 的所有n元组的 $(x_{1},x_{2},\cdots x_{n})$ 的集合。如果存在某个 $k(1\leqslant k \leqslant n)$ 使得 $x_{j}=y_{j}$ 对于 $1\leqslant j< k$ 恒成立，而 $x_{k}\prec y_{k}$ ，那么定义 $(x_{1},x_{2},\cdots ,x_{n})\prec (y_{1},y_{2},\cdots ,y_{n})$ 。 $\prec$ 是 $T_{n}$ 的一个良序关系吗？

（e）接（d），令 $T=\bigcup _{n\geq 1}T_{n}$ 。如果对于某个 $k\leq min(m,n)$ ， $x_{j}=y_{j}$ 对于 $1\leq j <k$ 恒成立，而 $x_{k}\prec y_{k}$ ；或者如果m<n，而 $x_{j}=y_{j}$ 对于 $1\leq j\leq m$ 恒成立，那么定义 $(x_{1},x_{2},\cdots ,x_{m})\prec (y_{1},y_{2},\cdots ,y_{n})$ 。 $\prec$ 是T的一个良序关系吗？

（f）证明： $\prec$ 是S的一个良序关系，当且仅当它满足上面的条件(i)和(ii)，并且不存在无穷序列 $x_{1},x_{2},x_{3},\cdots$ 满足 $j\geq 1$ 时恒有 $x_{j+1}\prec x_{j}$ 。

（g）令S按照 $\prec$ 是良序的，令P(x)是关于S中的元素x的一个命题。证明：如果在P(y)对于所有y $\prec$ x均为真的假定下能够证明P(x)，那么P(x)对于S中的所有x为真。

[注记：（g）部分是前面提到的简单归纳法的推广。在S为正整数集合时，它就是正文中讨论的数学归纳法这种简单情形。此时要求证明，如果P(y)对于正整数y<1均为真，那么P(1)为真；这无异于直接要求证明P(1)，因为P(y)对于所有这样的y（空集）必定为真。由此可知，在很多情况下无须单独论证P(1).

把（d）同（g）结合起来，就得到了n元归纳法的强有力的方法，用于证明关于n个正整数 $m_{1},\cdots ,m_{n}$ 的命题 $P(m_{1},\cdots m_{n})$ 。

（f）部分在计算机算法中有进一步应用：如果把一道计算的每个状态x映射到属于良序集S的元素 $f(x)$ ，使得计算的每一步能够把状态x变成状态y，且有 $f(y)\prec f(x)$ ,那么算法必定终止。这个原理推广了此前证明算法1.1E终止时使用的n值严格递减的论证。]

解：（a）在（iii）中令A=S；每个非空的良序集都是最小元素。

（c）不是，所有正实数的子集不满足（iii）。[注记：利用所谓“选择公理”可以给出一个比较复杂的论证，证明每个集合都存在某种良序关系，但是目前无人能够显示定义实数上的良序关系。]

（d）为了对 $T_{n}$ 证明（iii）,对n归纳：令A为 $T_{n}$ 的一个非空子集，考虑有A中元素的第一个分量组成的集合 $A_{1}$ ,由于 $A_{1}$ 是S的非空子集，而且S是良序的，因此 $A_{1}$ 中存在最小的元素x。现在考虑A中的第一个分量为x的元素构成的子集 $A_{x}$ ，去掉 $A_{x}$ 各元素的第一个分量后，可将它视为 $T_{n-1}$ 的一个子集，所以根据归纳法， $A_{x}$ 中存在最小元素 $(x,x_{2},\cdots ,x_{n})$ ，实际上这就是A的一个元素。

（e）不是，不过性质（i）和（ii）成立。如果S包含至少两个不同的元素a $\prec$ b，那么由(b),(a,b),(a,a,b),(a,a,a,b),(a,a,a,a,b),...组成的集合没有最小元素，当m<n时，或者当m=n且在 $T_{n}$ 中有 $(x_{1},\cdots ,x_{m})\prec (y_{1},\cdots y_{n})$ 时，定义 $(x_{1},\cdots ,x_{n}) \prec (y_{1},\cdots y_{n})$ ，那么T是良序的。

（f）令S按照 $\prec$ 是良序的。如果存在这样的一个无穷序列，那么由序列各项组成的集合A不满足性质(iii)，因为序列中没有最小元素。反过来，如果 $\prec$ 是满足(i)和(ii)但是不满足(iii)的关系，令A是S的不含最小元素的非空子集。由于A不空，A中存在 $x_{1}$ ；由于 $x_{1}$ 不是A的最小元素，在A中存在 $x_{2}$ 满足 $x_{2}$ $\prec$ $x_{1}$ ；由于 $x_{2}$ 也不是最小元素，又存在 $x_{3}\prec x_2$ ；以此类推。