1.[00] 最小的正有理数是多少?
解:不存在。如果r是正有理数,r/2总是更小的正有理数。
2.[00] 1+0.239999999...是一个十进制展开式吗?
解:假如末尾连续出现无限多个9,就不是十进制展开式。按照式(2),此时对应的十进制展开式为
3.[02]  是多少?
是多少?
解:,但是正文没有对它给出定义。
4.[05] 是多少?
是多少?
解:=
=
=
=
=
5.[05]我们通过十进制展开式定义了实数。讨论怎样改用二进制展开式定义实数,并且给出替代式(2)的定义。
解:式(2)
6.[10] 令 和
和 为实数。基于十进制表示,给出用来判定x=y,x<y还是x>y的规则。
为实数。基于十进制表示,给出用来判定x=y,x<y还是x>y的规则。
解:一个数的十进制展开式是唯一的,所以当且仅当m=n而且对于所有有
时,x=y。我们可以依次比较m与n,
与
,
与e_{2},等等,当第一次出现不相等的情况时,较大的数字所在的实数就是
中较大的数。
7.[M23]已知x和y为整数,从式(4)给出的定义出发,证明指数定律。
式(4) ,
, 如果
如果 ,
, 如果
如果 。
。
解:可以对x归纳,首先证明x为正数时定律成立,然后证明x为负数是定律成立,细节从略。
8.[25]令m为正整数。证明每个正实数u有唯一的m次正根,做法是给出一种方法,依次构造根的十进制展开式中的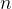 ,
,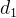 ,
,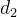 ,
,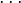 的值。
的值。
解:依次令可求出满足
的n值。归纳假设已经求出
,那么
是满足
的数字。按这种构造方法,对于所有的k>l都不满足,因为此情况出现的必要条件是
。
9.[M23] 假定当x和y为整数时指数定律成立,证明x和y为有理数时指数定律成立。
解:。因此
。这证明了第二定律。用第二定律可以证明第一定律:
。
10.[18] 证明 不是有理数。
不是有理数。
解:如果,,其中p和q为正整数,那么
。而这是不可能的,因为等式右端能被5整除,左端却不能。
11.[10]如果 ,为了确定
,为了确定 的十进制展开式的前3位小数,我们需要知道多少位精度的x值?[注记:可以利用习题10的结果。]
的十进制展开式的前3位小数,我们需要知道多少位精度的x值?[注记:可以利用习题10的结果。]
解:无限多位!如果x的各位数字同一致,无论给出多少位数,我们都不知道
还是
这丝毫没有神秘难解或者自相矛盾之处。加法也有类似的情况,假如把
加到
上。
12.[02] 解释式(10)为什么可由式(8)推出。
解:只有如此取值才满足等式(7)。
13.[M23] (a)已知x是正实数,n是正整数,证明不等式![\sqrt[n]{1+x}-1\leq x/n](https://latex.csdn.net/eq?%5Csqrt%5Bn%5D%7B1+x%7D-1%5Cleq%20x/n) 。(b)利用这个结果解释式(7)后面的说明。
。(b)利用这个结果解释式(7)后面的说明。
解:(a)首先用归纳法证明:如果,那么
。然后置
,并且去n次根。(b)
。
14.[15] 证明式(12)。
式(12),如果c>0。
解:在(5)的第二个等式中置,然后两端同时取对数。
15.[10]证明或证伪:
 ,如果
,如果 。
。
解:把“”移到等式的另一端,利用式(11)证明结论成立。
,如果x>0,y>0
16.[00] 怎样用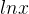 和
和 表示
表示 ?
?
解:由式(14),是。
式(14)
17.[05] 计算: ;
; ;
; ;
; ;
; 。
。
解:5;1;1;0;无意义。
18.[10]证明或证伪 。
。
解:原式不成立,
19.[20] 如果整数n的十进制表示长14位数,n的值能否存入容量为47个二进制和一个符号位的一个计算机字?
解:是,因为。
20.[10] 在 与
与 之间是否存在简单的关系?
之间是否存在简单的关系?
解:它们互为倒数。
21.[15] (对数的对数)用 表示
表示 。
。
解:
22.[20](理查德 汉明)证明
汉明)证明 。且误差小于1%!(因此利用自然对数表和常用对数表也可以获得二进制对数的近似值。)
。且误差小于1%!(因此利用自然对数表和常用对数表也可以获得二进制对数的近似值。)
解:由附录A的表,,
。
相对误差0.582 %
23.[M25]根据图6,给出 的几何证明。
的几何证明。
解:在图6中,取面积为的图形,用x除它的高度,同时用x乘它的长度。这个变形保持它的面积不变,并使它与从
减去
剩下的图形全等,因为在
的图中,
点处的高度为
。
24.[15] 说明怎样修改本小节最后用于计算以10为底的对数的方法,使之能计算以2为底的对数。
解:用2代换所有10。
25.[22] 假定我们有一台二进制的计算机和一个数x, 。说明利用下面的算法,可以计算
。说明利用下面的算法,可以计算 的近似值,仅需使用同所需精度的小数位数成正比的移位、加法、减法运算:
的近似值,仅需使用同所需精度的小数位数成正比的移位、加法、减法运算:
L1.[初始化] 置,
右移1位,
。
L2.[检验算法终结]如果,终止。
L3.[比较]如果,置
右移1位,
,重复这一步。
L4.[减少值]置,
右移k位,
,然后转到L2.丨
[注记:这个方法同计算机硬件中做除法的方法非常类似。其原始思想要追溯到亨利.布里格斯,他以此方法计算的对数表于1624年出版(当时他用的是十进制而不是二进制)。我们需要一份包含等常数的辅助表,位数要与计算机精度相同。算法有意由数字向右移位引入计算误差,以保证最终x减少到1而使算法终止。这道习题意在说明这个算法为何会终止,为何能计算出
的近似值。]
解:注意到,其中p表示精度(小数点后的二进制数的位数)。算法执行时,
的值基本不变。
26.[M27] 根据算数运算中用到的精度,对于上题算法的固有误差求出一个严格的上界。
解:
27.[M25] 考虑正文中讨论的计算 的方法。令
的方法。令 表示计算到
表示计算到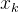 时的近似值,定义如下:
时的近似值,定义如下: 。在用式(18)计算
。在用式(18)计算 时,用
时,用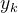 代替
代替 ,其中
,其中 ,且
,且 。这里
。这里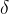 和
和 是很小的常数,反映由于舍入或者截断而产生的误差的上界和下界。如果用
是很小的常数,反映由于舍入或者截断而产生的误差的上界和下界。如果用 表示计算的结果,证明在k步之后有
表示计算的结果,证明在k步之后有
 。
。
解:对k归纳证明:
并对上式取对数。
28.[M30] (理查德 费曼)建立当
费曼)建立当 时计算
时计算 的一种方法,仅使用移位、加法和减法(类似于习题25的算法),并且分析它的精度。
的一种方法,仅使用移位、加法和减法(类似于习题25的算法),并且分析它的精度。
解:下面的解法使用同习题25一样的辅助表。
E1.[初始化。]置,其中
是x可能取的最大值,
是最接近
的近似值。(
的值在下列步骤中基本不变。)
E2.[检验算法终结。]如果x=0,终止。
E3.[比较。]如果,k增加1,重复这一步。
E4.[减少值。]置,
右移k位
,然后转到E2。丨
如果在步骤E1将y取为,那么在步骤E4的第j次执行中,由于置
和
,
和
是微小误差,因此就引入了计算误差。算法终结时,计算出
。进一步的分析依赖于b和计算机的字大小。请注意,在本题和习题26中,若改成以e为底,可改进误差估计,因为对于k的多数值,表项
可以给出高精度的值:它等于
。
注记:对应三角函数可给出类似的算法,见约翰麦基特,IBM J. Res. and Dev. 6(1962),210-226;7(1963),237-245. 令见陈天机,IBM J. Res. and Dev.16(1972),380-388;弗拉季斯拉夫
林斯基,Vychisl.Mat.2(1957),90-119;高德纳,METAFONT:The Program(Reading,Mass.:Addison-Wesley,1986),
。
29.[HM20] 给定大于1的实数x。(a)实数b>1取什么值时, 取到最小值?(b)整数b>1取什么值时,
取到最小值?(b)整数b>1取什么值时, 取到最小值?(c)整数b>1取什么值时,
取到最小值?(c)整数b>1取什么值时, 取到最小值?
取到最小值?
解:e;3;4。
30.[12]假定n>1且 ,化简表达式
,化简表达式 。
。
解:n。























 398
398

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










