【题目描述】
输入三角形3条边的长度值(均为正整数),判断是否能为直角三角形的3个边长。如果可以,则输出yes,如果不能,则输出no。如果根本无法构成三角形,则输出not a triangle。
【题目来源】
刘汝佳《算法竞赛入门经典 第2版》习题1-6 三角形(triangle)
【解析】
一、问题求解
假设三边边长为a、b、c(a、b、c>0如下图),则:
1)构成直角三角形的充分必要条件:如a≤c,b≤c,则 。
2)构成三角形的充分必要条件:如a≤c,b≤c,则a+b>c。

关于这两个条件的证明,见后文。
所以这道题分两步:
1)找出最大值c。
2)按上述条件判断能构成哪种图形。
下面分开讨论:
步骤1)找出最大值c。
为什么第一步是找出最大值?因为上述两个条件都有一个共同的前提:a<c,b<c。也就是a和b谁大谁小无所谓,但都要小于c。这种情况下如果将三个数排序的话当然也是没有任何问题的,但更高效的方法是直接找出最大值c。
方法就是让c分别与a、b比较,如果c小于a、b就交换变量,从而使c成为3个数的最大值。
步骤2)判断构成图形。
直角三角形是特殊的三角形,按一般的理解,应该先判断大类,再判断小类,即先判断是否能构成三角形,如果能,再判断是否是直角三角形。
但勾股定理是直角三角形的充分必要条件,通过这一个条件即可判断能否构成直角三角形,而不需要先判断能否构成三角形。
所以从效率的角度看,应该先判断是否是直角三角形,后判断是否构成三角形。这样如果是直角三角形的话,就可以直接输出结果,不用再做后面的判断了。
C代码如下:
#include<stdio.h>
int main(){
int a, b, c, t;
scanf("%d%d%d", &a, &b, &c);
//将c变为最大值
if(c<a){
t=a; a=c; c=t;
}
if(c<b){
t=b; b=c; c=t;
}
//判断是否能构成直角三角形
if(a*a+b*b==c*c){
printf("yes\n");
} else if(a+b>c){
printf("no\n");
}else{
printf("not a triangle\n");
}
return 0;
}
注:如果本题只是判断是否构成三角形,那就不用再找出最大值,而直接根据三角形的构成条件“任意两边之和大于第三边”判断即可。代码如下:
if(a + b > c && a + c > b && b + c > a) printf("构成三角形\n");
算法方面的问题就说完了,仅关注算法的可以到此为止。
二、构成直角三角形和三角形的条件证明
1、三角形构成条件证明:
在初中数学教材中,只给出了“三角形的两边之和大于第三边”的证明。
证明:对于任意一个△ABC,如果把其中任意两个顶点(例如B、C)看成定点,由“两点之间,线段最短”可得:AB+AC>BC

同理有:
AC+BC>AB,AB+BC>AC
即:三角形的两边之和大于第三边。
这个结论等同于:三角形⇒两边之和大于第三边,即只证明了“三角形”是“两边之和大于第三边”的充分条件。
实际上,它的逆命题也是成立的,即如果任意两边之和大于第三边⇒三角形,这就是能构成三角形的条件。
我们知道,如果由A可以推出B,由B可以推出A,则A是B的充要条件,所以“任意两边之和大于第三边”是构成三角形的充分必要条件。
下面来证明这个逆命题:
1)简化命题。
“任意两边之和大于第三边”这个命题听起来像一统江湖的任我行教主一样霸道,实际上只不过是吹起来泡沫,就像把小米粒大的黄金镀到铜上变成金砖一样。更夸张的是,并不是只变成一块金砖,而是三块:a+b>c,a+c>b,b+c>a。
注意,这三个条件是“与”的关系,即他们要同时成立,然后去证明能构成三角形。
这显然有些复杂,让人不知道从哪下手。根本原因在于它只给出了三个变量的相互关系,不知道两个变量之间及单个变量的关系。这和三元一次方程比二元一次方程、一元一次方程难解是一个道理。
不难看出,“任意两边之和大于第三边”这个命题只适合作结论,不适合作条件。
所以,首先我们要将这个条件进行简化,把它转化成一个更简单的等价命题:两边之和大于最长边。这其实很好理解,如果第三边不是最长边,显然其他两边中至少有一边是大于第三边的,故另外两边之和一定大于第三边,所以只需考虑第三边是最长边的情况即可。
上述结论用不等式也可以证明:
设c为最长边,a、b为较短边,则已知条件为:0<a≤c,0<b≤c,a+b>c。
由a+c>c,0<b≤c得a+c>b;由b+c>c,0<a≤c得b+c>a。
由以上可知,归根到底,“两边之和大于最长边”才是构成三角形的充要条件,而“任意两边之和大于第三边”只不过是由“两边之和大于最长边”镀成的金砖。
2)证明。
设c为最长边,a、b为较短边,则已知条件为:0<a≤c,0<b≤c,a+b>c。
把a、b、c想象成三根木棍,现在把最长的木棍c用胶水粘牢在桌面上(即看作固定边),把a、b两根木棍的一头固定到c的两个端点上,另一头可以在桌面上随意摆动,显然它们划过的轨迹是一个分别以A、B为圆点,以a、b为半径的圆。那么只要证明这两个圆是相交的(即存在图中的C、D交点),就能证明这三个边可以构成三角形。

两圆相交的充要条件是:圆心距小于两圆半径之和,大于两圆半径之差。
c就是两圆圆心距,a、b就是两圆半径。
因为a+b>c,所以满足圆心距小于两圆半径之和。
因为0<a≤c,0<b≤c,所以a-b≤c-b<c,b-a≤c-a<c,即圆心距大于两圆半径之差。
故两圆相交,存在交点C、D,连接AC、BC,构成△ABC,且AC=b,BC=b,AB=c,故这三个边可以构成三角形。
2、直角三角形构成条件证明:
关于勾股定理和其逆定理,初中数学教材中都有完整的证明。
(1) 勾股定理:如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么 。
下面介绍教材中的“赵爽弦图”证明方法,这种方法是我国汉代的赵爽在注解《周髀算经》时提出的。
证明过程如下:
把边长为a、b的两块正方形木板边挨边对齐,用哥俩好将接缝处粘牢。按下图画线、上色,将整块木板分为四个一样的直角三角形(红色)和一个正方形(黄色)。沿下图斜线将木板切开。

将切下的两个红色直角三角形以一个华丽的转身移至图形上方如图位置,再用哥俩好粘牢。

最后形成这样一个优美的图形,它就是“赵爽弦图”。整个图形由原来的以a、b为边长的两个正方形变成一个以直角三角形斜边c为边长的正方形。

好了,整个过程就是一次手工制作,至此咱们已经完成了勾股定理的证明。
是的,证明完了,几乎不需要多余的解释。下面的文字描述与如此精妙的方法比起来显得那样的苍白无力:
原来两个正方形的面积和为 ,“切割重拼”后形成的大正方形面积是
,整个过程面积未发生改为,所以
。
(2) 勾股定理的逆定理:如果三角形的三边长a,b,c满足 ,那么这个三角形是直角三角形。

这个证明过程很简单,但是思路非常有创意。
就是先画一个两条直角边长分别为a,b的直角三角形,然后由勾股定理可知其斜边等于c,这样这个直角三个形与要证的三角形三条对边相等,故两个三角形全等,从而得出要证的三角形为直角三角形。
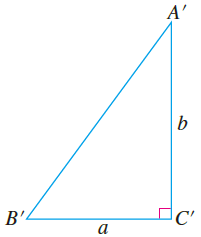




























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










