| 日期 | 内容 |
|---|---|
| 2024.9.19 | 平面几何 |
| 2024.9.20 | 直角三角形,等腰三角形,等边三角形 |
| 2024.9.26 | 等高模型 ,四边形菱形,梯形,圆和扇形 |
| 2024.9.27 | 立体几何 |
| 2024.9.27 | 正方体,长方体,柱体,圆柱,棱柱,球体 |
| 2024.9.29 | 平面解析几何 |
| 2024.9.29 | 点与直线,两直线关系,圆,圆与圆,圆与直线 |
【1.历年真题】
【2020.16】在 △ A B C △ABC △ABC中, ∠ B = 60 ° ∠B=60° ∠B=60°,则 c a > 2 \frac{c}{a}>2 ac>2()
(1) ∠ C < 90 ° ∠C<90° ∠C<90°
(2) ∠ C > 90 ° ∠C>90° ∠C>90°
解题:
两条件结果不一致,属于A或B型。
当为直角三角形时 c a = 2 \frac{c}{a}=2 ac=2,锁定分母底边 a a a不动,将 c c c延长,则三角形变为钝角三角形, ∠ C > 90 ° ∠C>90° ∠C>90°
答案B
【2013.07】如图 A B = A C = 5 , B C = 6 , E AB=AC=5,BC=6,E AB=AC=5,BC=6,E是 B C BC BC的中点, E F ⊥ F C EF⊥FC EF⊥FC则 E F EF EF=()
A.1.2
B.2
C.2.2
D.2.4
E.2.5
解题:
A E ∗ E C = A C ∗ E F , E F = 2.4 AE*EC=AC*EF,EF=2.4 AE∗EC=AC∗EF,EF=2.4
答案D
【2023.11】如图在三角形 A B C 中 ABC中 ABC中, ∠ B A C = 60 ° , B D ∠BAC=60°,BD ∠BAC=60°,BD平分 ∠ A B C , ∠ABC, ∠ABC,交 A C AC AC于 D , C E D,CE D,CE平分 ∠ A C B ∠ACB ∠ACB交 A B AB AB于 E , B D E,BD E,BD和 C E CE CE交于 F , F, F,则 ∠ E F B = ∠EFB= ∠EFB=()
A.45°
B.53.5°
C.60°
D.67.5°
E.75°
解题:
题目中涉及到“如图”字样求角度问题:量角器大法
三角形没有特殊说明,其中一个角为60度,那么就按照等边三角形进行假设
∠ E F B = 60 ° ∠EFB=60° ∠EFB=60°
答案C
【2008.05】如图 △ A B C △ABC △ABC的面积为 1 1 1, △ A E C ,△ D E C ,△ B E D △AEC,△DEC,△BED △AEC,△DEC,△BED的面积相等,则 △ A E D △AED △AED的面积为=()
A. 1 3 \frac{1}{3} 31
B. 1 6 \frac{1}{6} 61
C. 1 5 \frac{1}{5} 51
D. 1 4 \frac{1}{4} 41
E. 2 5 \frac{2}{5} 52
解题:
问题不具体,可以把三角形假设为一个等边三角形
A E : E C = 1 : 2 且等高,所以△ A E D = 1 3 ∗ 1 2 = 1 6 AE:EC=1:2且等高,所以△AED=\frac{1}{3}*\frac{1}{2}=\frac{1}{6} AE:EC=1:2且等高,所以△AED=31∗21=61
答案B
【2023.03】如图所示,已知 A E = 3 A B , B F = 2 B C . AE=3AB,BF=2BC. AE=3AB,BF=2BC.若 △ A B C △ABC △ABC的面积为 2 2 2则 △ A E F △AEF △AEF的面积为()
A.14
B.12
C.10
D.8
E.6
解题:
△ A B C 与△ A B F 等高 A B 且 B F = 2 B C △ABC与△ABF等高AB且BF=2BC △ABC与△ABF等高AB且BF=2BC
△ A B C : △ A B F = 2 : 4 , 所以 S △ A B F = 4 △ABC:△ABF=2:4,所以S_△ABF=4 △ABC:△ABF=2:4,所以S△ABF=4
因为 A E = 3 A B 因为AE=3AB 因为AE=3AB
△ A B F : △ A E F = 1 : 3 △ABF:△AEF=1:3 △ABF:△AEF=1:3
所以 S △ A B F = 12 所以S_△ABF=12 所以S△ABF=12
答案B
【2020.10】如图,在 △ A B C △ABC △ABC中, ∠ A B C = 30 ° ∠ABC=30° ∠ABC=30°,将线段 A B AB AB绕点 B B B旋转至 D B DB DB,使 ∠ D B C = 60 ° ∠DBC=60° ∠DBC=60°则 △ D B C △DBC △DBC与 △ A B C △ABC △ABC的面积之比为()
A.1
B. 2 \sqrt2 2
C.2
D. 3 2 \frac{\sqrt3}{2} 23
E. 3 \sqrt3 3
解题:
面积比=高比
答案E
【2012.03】若菱形两条对角线的长分别为6和8,则这个菱形的周长和面积分别为()
解题:
两对角线都除以2得其中一组三角形直角边长,分别为3和4,则斜边为5
周长= 5 ∗ 4 = 20 5*4=20 5∗4=20
面积= 6 ∗ 8 2 = 24 \frac{6*8}{2}=24 26∗8=24
【2011.18】如图所示,等腰梯形的上底与腰均为 x x x,下底为 x + 10 x+10 x+10,则 x = 13. x=13. x=13.()
(1)该梯形的上底与下底之比为 13 : 23 13:23 13:23
(2)该梯形的面积为 216 216 216
解题:
蒙猜选择D
条件(1) x x + 10 = 13 23 , 解得 x = 13 \frac{x}{x+10}=\frac{13}{23},解得x=13 x+10x=2313,解得x=13条件充分
条件(2)做垂线
{ 梯形面积 = (上底 + 下底) ∗ h 2 = ( x + x + 10 ) ∗ h 2 = 216 h 2 = x 2 − 5 2 假设 x = 13 \begin{cases} 梯形面积=\frac{(上底+下底)*h}{2}=\frac{(x+x+10)*h}{2}=216\\ h^2=x^2-5^2\\ 假设x=13 \end{cases} ⎩ ⎨ ⎧梯形面积=2(上底+下底)∗h=2(x+x+10)∗h=216h2=x2−52假设x=13
求得h=12条件2充分
答案D
【2020.12】如图圆O的内接 △ A B C △ABC △ABC是等腰三角形,底边 B C = 6 BC=6 BC=6,顶角为 π 4 , \frac{π}{4}, 4π,则圆O的面积为()
A. 12 π 12π 12π
B. 16 π 16π 16π
C. 18 π 18π 18π
D. 32 π 32π 32π
E. 36 π 36π 36π
解题:
顶角 ∠ B A C = π 4 ∠BAC=\frac{π}{4} ∠BAC=4π则 ∠ B O C = π 2 = 90 ° ∠BOC=\frac{π}{2}=90° ∠BOC=2π=90°
推出 △ B O C △BOC △BOC为等腰直角三角形,又因为 B C = 6 BC=6 BC=6则半径 r = 3 2 r=3\sqrt2 r=32
则圆O的面积为 π r 2 = π ( 3 2 ) 2 = 18 π πr^2=π(3\sqrt2)^2=18π πr2=π(32)2=18π
答案C
【2014.13】如图所示,大小两个半圆的直径在同一直线上,弦 A B AB AB与小半圆相切,且与直径平行,弦 A B AB AB长为 12 12 12,则图中阴影部分面积为()
A. 24 π 24π 24π
B. 21 π 21π 21π
C. 18 π 18π 18π
D. 15 π 15π 15π
E. 12 π 12π 12π
解题:
将两个圆变为同心圆。
S 阴影面积 = S 大半圆 − S 大半圆 = 1 2 π ( R 2 − r 2 ) = 18 π S_{阴影面积}=S_{大半圆}-S_{大半圆}=\frac{1}{2}π(R^2-r^2)=18π S阴影面积=S大半圆−S大半圆=21π(R2−r2)=18π
答案C
【2017.13】将长,宽,高分别为 12 , 9 , 6 12,9,6 12,9,6的长方体切割成正方体,且切割后无剩余,则能切割成相同的正方体的最少个数为().
A.3
B.6
C.24
D.96
E.64
解题:
可以画图也可以通过求最大公约数为3
9 和 6 组成的面可以切 6 个等分正方形 9和6组成的面可以切6个等分正方形 9和6组成的面可以切6个等分正方形
12 可以分成 4 份 12可以分成4份 12可以分成4份
6 ∗ 4 = 24 6*4=24 6∗4=24
答案C
【2020.21】能确定长方体的体对角线().
(1)已知长方体一个顶点的三个面的面积.
(2)已知长方体一个顶点的三个面的对角线.
解题:
条件(1)已知 a b , a c , b c ab,ac,bc ab,ac,bc可以解得 a , b , c a,b,c a,b,c的具体值,条件充分。
条件(2)已知 a 2 + b 2 , a 2 + c 2 , b 2 + c 2 \sqrt {a^2+b^2},\sqrt {a^2+c^2},\sqrt {b^2+c^2} a2+b2,a2+c2,b2+c2可以解得 a , b , c a,b,c a,b,c的具体值,条件充分。
答案D
【2015.06】有一根圆柱形铁管,管壁厚度为0.1m,内径为1.8m,长度为2m,若将该铁管熔化后浇铸成长方体,则该长方体的体积为(单位: m 3 , π ≈ 3.14 m^3,π≈3.14 m3,π≈3.14)().
A.0.38
B.0.59
C.1.19
D.5.09
E.6.28
解题:
管内半径 r = 1.8 2 = 0.9 m r=\frac{1.8}{2}=0.9m r=21.8=0.9m
管外半径 R = 0.9 + 0.1 = 1 m R=0.9+0.1=1m R=0.9+0.1=1m
浇铸体积 V = ( π R 2 − π r 2 ) h = π ( R 2 − r 2 ) h = 3.14 ( 1 − 0.81 ) 2 = 1.19 V=(πR^2-πr^2)h=π(R^2-r^2)h=3.14(1-0.81)2=1.19 V=(πR2−πr2)h=π(R2−r2)h=3.14(1−0.81)2=1.19
“若将该铁管熔化后浇铸成长方体“为误导文字,实际浇铸成任何形状都没关系
答案C
【2014.14】某工厂在半径为5cm的球形工艺品上镀一层装饰金属,厚度为0.01cm,已知装饰金属的原材料是棱长为20cm的正方体锭子,则加工10000个该工艺品需要的锭子数量最少为, π ≈ 3.14 π≈3.14 π≈3.14().
A.2
B.3
C.4
D.5
E.20
解题:
常规解法, V 大球 − V 小球 , 但计算量比较大,换成球面积 ∗ 镀层 h 的思路 常规解法,V_{大球}-V_{小球},但计算量比较大,换成球面积*镀层h的思路 常规解法,V大球−V小球,但计算量比较大,换成球面积∗镀层h的思路
球面积 S 球 = 4 3 π r 2 S_球=\frac{4}{3}πr^2 S球=34πr2
镀层厚的体积 V 镀层 = S 球 ∗ h = 4 3 π 5 2 ∗ 0.01 ∗ 10000 V_{镀层}=S_球*h=\frac{4}{3}π5^2*0.01*10000 V镀层=S球∗h=34π52∗0.01∗10000
求解与 n ∗ 2 0 3 进行比较 n*20^3进行比较 n∗203进行比较
得 n ≈ 4 n≈4 n≈4
答案C
【2014.16】已知曲线 l : y = a + b x − 6 x 2 + x 3 l:y=a+bx-6x^2+x^3 l:y=a+bx−6x2+x3则 ( a + b − 5 ) ( a − b − 5 ) = 0 (a+b-5)(a-b-5)=0 (a+b−5)(a−b−5)=0().
(1)曲线l过点(1,0).
(2)曲线l过点(-1,0).
解题:
看题干可能有点懵逼,每关系,直接将已知条件带进方程
条件(1) 0 = a + b − 6 + 1 = a + b − 5 ,符合 ( a + b − 5 ) ( a − b − 5 ) = 0 ,条件充分。 0=a+b-6+1=a+b-5,符合(a+b-5)(a-b-5)=0,条件充分。 0=a+b−6+1=a+b−5,符合(a+b−5)(a−b−5)=0,条件充分。
条件(2) 0 = a − b − 6 + 1 = a + b − 7 ,不符合 ( a + b − 5 ) ( a − b − 5 ) = 0 ,条件不充分。 0=a-b-6+1=a+b-7,不符合(a+b-5)(a-b-5)=0,条件不充分。 0=a−b−6+1=a+b−7,不符合(a+b−5)(a−b−5)=0,条件不充分。
答案A
【2023.07】如图,已知点 A ( − 1 , 2 ) A(-1,2) A(−1,2),点 B ( 3 , 4 ) B(3,4) B(3,4)若点 P ( m , 0 ) P(m,0) P(m,0)使得 ∣ P B ∣ − ∣ P A ∣ |PB|-|PA| ∣PB∣−∣PA∣最大,则().
A. m = − 5 m=-5 m=−5
B. m = − 3 m=-3 m=−3
C. m = − 1 m=-1 m=−1
D. m = 1 m=1 m=1
E. m = 3 m=3 m=3
解题:
点 P , A , B P,A,B P,A,B不在一条直线时, P A , P B , P C PA,PB,PC PA,PB,PC构成三角形
则有两边之差<第三边
∣ P B ∣ − ∣ P A ∣ < ∣ A B ∣ |PB|-|PA|<|AB| ∣PB∣−∣PA∣<∣AB∣
那么就是说当|AB在同一条直线上时, ∣ P B ∣ − ∣ P A ∣ |PB|-|PA| ∣PB∣−∣PA∣取得最大值
根据两点公式 y − 2 4 − 2 = x − ( − 1 ) 3 − ( − 1 ) \frac{y-2}{4-2}=\frac{x-(-1)}{3-(-1)} 4−2y−2=3−(−1)x−(−1)
整理得 x − 2 y + 5 = 0 , 带入 P 点坐标, x = − 5 x-2y+5=0,带入P点坐标,x=-5 x−2y+5=0,带入P点坐标,x=−5
答案A
【2016.10】圆 x 2 + y 2 − 6 x + 4 y = 0 x^2+y^2-6x+4y=0 x2+y2−6x+4y=0上到原点距离最远的点是().
A. ( − 3 , 2 ) (-3,2) (−3,2)
B.3
C.4
D.5
E.20
解题:
常规解法, V 大球 − V 小球 , 但计算量比较大,换成球面积 ∗ 镀层 h 的思路 常规解法,V_{大球}-V_{小球},但计算量比较大,换成球面积*镀层h的思路 常规解法,V大球−V小球,但计算量比较大,换成球面积∗镀层h的思路
球面积 S 球 = 4 3 π r 2 S_球=\frac{4}{3}πr^2 S球=34πr2
镀层厚的体积 V 镀层 = S 球 ∗ h = 4 3 π 5 2 ∗ 0.01 ∗ 10000 V_{镀层}=S_球*h=\frac{4}{3}π5^2*0.01*10000 V镀层=S球∗h=34π52∗0.01∗10000
求解与 n ∗ 2 0 3 进行比较 n*20^3进行比较 n∗203进行比较
得 n ≈ 4 n≈4 n≈4
答案C
【2.MBA大师例题】
【例题1】三条线段 a = 5 , b = 3 , c a=5,b=3,c a=5,b=3,c的值为整数,以 a , b , c a,b,c a,b,c为边的三角形有()个.
A.1
B.3
C.5
D.7
E.以上都不对
解题:
∣ a − b ∣ < c < a + b |a-b|<c<a+b ∣a−b∣<c<a+b
2 < c < 8 、且 c 为整数 2<c<8、且c为整数 2<c<8、且c为整数
则 c = 3 , 4 , 5 , 6 , 7 、共有 5 个结果 则c=3,4,5,6,7、共有5个结果 则c=3,4,5,6,7、共有5个结果
答案C
【例题2】已知三条线段的长度分别为 a , b , c a,b,c a,b,c,并且 a > b > c a>b>c a>b>c,则还需要满足哪个条件,才能确定这三条线段可以组成三角形().
A. a + b > c a+b>c a+b>c
B. a + c > b a+c>b a+c>b
C. a − b < c a-b<c a−b<c
D. b − c > a b-c>a b−c>a
E. a − b > c a-b>c a−b>c
解题:
a > b > c > 0 a>b>c>0 a>b>c>0 & { a + b > c , 满足 a + c > b , 满足 b + c > a , 不一定( a b c 指线段,不指三角形) \begin{cases} a+b>c,满足\\ a+c>b,满足\\ b+c>a,不一定(abc指线段,不指三角形) \end{cases} ⎩ ⎨ ⎧a+b>c,满足a+c>b,满足b+c>a,不一定(abc指线段,不指三角形)
满足三角形条件任意两边之和大于第三边, b + c > a = a − b < c 满足三角形条件任意两边之和大于第三边,b+c>a=a-b<c 满足三角形条件任意两边之和大于第三边,b+c>a=a−b<c
答案C
【例题3】若一个三角形的周长为偶数,且已知两边长分别为 6 6 6和 2017 2017 2017则满足条件的三角形共有()个.
A.3
B.4
C.5
D.6
E.7
解题:
设第三边满足 2017 − 6 < c < 2017 + 6 2017-6<c<2017+6 2017−6<c<2017+6
则 2011 < c < 2023 2011<c<2023 2011<c<2023
因为周长为偶数,结合另外两边之和为奇数,则第三边也应该为奇数
则 c = 2013 , 2015 , 2017 , 2019 , 2021 共 5 个 c=2013,2015,2017,2019,2021共5个 c=2013,2015,2017,2019,2021共5个
答案C
【例题4】在 △ A B C 中, A B = 4 , A C = 8 △ABC中,AB=4,AC=8 △ABC中,AB=4,AC=8则 △ A B C △ABC △ABC的面积取值范围为().
A.(0,32]
B.(0,18]
C。[0,16]
D.(0,16]
A.(0,16)
解题:
直角三角形时,高最大
△ A B C M A X = 1 2 A C ∗ A B = 1 2 4 ∗ 8 = 16 △ABC_{MAX}= \frac{1}{2}AC*AB=\frac{1}{2}4*8=16 △ABCMAX=21AC∗AB=214∗8=16
答案D
【例题5】三角形的三条边长分别为 a , b , c 、△ A B C a,b,c、△ABC a,b,c、△ABC为直角三角形().
(1) △ A B C △ABC △ABC的三边长之比为 1 : 2 : 3 1:\sqrt2:\sqrt3 1:2:3
(2) △ A B C △ABC △ABC的面积 S = 1 2 a b S=\frac{1}{2}ab S=21ab
解题:
条件(1) 1 2 + ( 2 ) 2 = ( 3 ) 2 1^2+(\sqrt2)^2=(\sqrt3)^2 12+(2)2=(3)2满足勾股定理,条件充分。
条件(2) S = 1 2 a b S=\frac{1}{2}ab S=21ab满足直角三角形判断,条件充分。
两条件单独都充分
答案D
【例题6】 △ A B C △ABC △ABC的三边长分别为 6 , 8 , 10 6,8,10 6,8,10那么最长边对应的高为().
A.4
B.4.5
C.4.8
D.5
E.6
解题:
6 , 8 , 10 6,8,10 6,8,10常用勾股数,能判断为直角三角形
两直角边相乘=斜边*斜边上的高
6 ∗ 8 = 10 ∗ h 6*8=10*h 6∗8=10∗h
h = 4.8 h = 4.8 h=4.8
答案C
【例题6】一个顶角为 30 ° 30° 30°的直角三角形,面积为 3 3 2 \frac{3\sqrt3}{2} 233,则三角形的周长为().
A. 3 \sqrt3 3
B. 3 3 3\sqrt3 33
C. 3 + 3 3+\sqrt3 3+3
D. 3 + 3 3 3+3\sqrt3 3+33
E. 2 + 2 3 2+2\sqrt3 2+23
解题:
30 ° 30° 30°直角三角形,对边是斜边一半
设三边之比为 a : 3 a : 2 a a:\sqrt3a:2a a:3a:2a
S △ = 1 2 a ∗ 3 a = 3 3 2 解得 a = 3 S_△=\frac{1}{2}a*\sqrt3a=\frac{3\sqrt3}{2}解得a=\sqrt3 S△=21a∗3a=233解得a=3
周长= a : 3 a : 2 a = 3 + 3 3 + 2 3 = 3 + 3 3 a:\sqrt3a:2a=\sqrt3+\sqrt3\sqrt3+2\sqrt3=3+3\sqrt3 a:3a:2a=3+33+23=3+33
答案D
【例题7】顶角是 150 ° 150° 150°的等腰直角三角形,腰上高的长与腰长的比是().
A. 1 : 3 1:3 1:3
B. 1 : 2 1:2 1:2
C. 1 : ( 2 + 3 ) 1:(2+\sqrt3) 1:(2+3)
D. 1 : 3 1:\sqrt3 1:3
E. 1 : ( 2 − 3 ) 1:(2-\sqrt3) 1:(2−3)
解题:
C D 为高 h ,且 ∠ D A C = 30 ° ,那么 C D = 1 2 A C = 1 : 2 CD为高h,且∠DAC=30°,那么CD=\frac{1}{2}AC=1:2 CD为高h,且∠DAC=30°,那么CD=21AC=1:2
答案B
【例题8】已知一等边三角形周长为 3 3 3\sqrt3 33,求它的面积和高。
解题:
周长 3 3 3\sqrt3 33,则推出边长为 3 \sqrt3 3
高 h = 3 2 ∗ 3 = 3 2 h=\frac{\sqrt3}{2}*\sqrt3=\frac{3}{2} h=23∗3=23
面积 S = 3 4 ∗ 3 2 = 3 4 3 S=\frac{\sqrt3}{4}*\sqrt3^2=\frac{3}{4}\sqrt3 S=43∗32=433
【例题9】如图所示,长方形 A B C D ABCD ABCD的两条边长分别为 8 m 和 6 m 8m和6m 8m和6m,四边形 O E F G OEFG OEFG的面积为 4 m 2 4m^2 4m2则阴影部分的面积为().
A. 32 m 2 32m^2 32m2
B. 28 m 2 28m^2 28m2
C. 24 m 2 24m^2 24m2
D. 20 m 2 20m^2 20m2
E. 16 m 2 16m^2 16m2
解题:
底同线+顶同线=等高模型
S △ A F C = S △ D F C S_△AFC=S_△DFC S△AFC=S△DFC
S △ B D F = S △ A B F S_△BDF=S_△ABF S△BDF=S△ABF
拉开后,空白面积多出一个四边形 O E F G OEFG OEFG,则阴影面积较少了一个 O E F G OEFG OEFG
阴影面积= 8 ∗ 6 + 4 = 28 8*6+4=28 8∗6+4=28
答案B
【例题10】如图所示,矩形 A D E F ADEF ADEF的面积为 16 16 16, △ A D B △ADB △ADB的面积为 3 3 3, △ A C F △ACF △ACF的面积为 4 4 4,则 △ A B C △ABC △ABC的面积为为().
A. 6 6 6
B. 7 7 7
C. 8 8 8
D. 6.5 6.5 6.5
E. 7.5 7.5 7.5
解题:
不具体问题,根据面积进行凑配即可,且C为FE中点。
答案D
【例题11】若一个圆与一个正方形的面积相等,则().
A.它们的周长相等
B.圆周长是正方形周长的 π π π倍
C.正方形的周长长
D.圆周长是正方形周长的 2 π 2\sqrtπ 2π倍
E.以上均不正确
解题:
以上均不正确选项慎选!往年没有这个答案是正确的!
设圆半径为 r r r,圆面积= π r 2 πr^2 πr2
正方形边长 a a a,正方形面积= a 2 a^2 a2
因为面积相等。所以 π r 2 = a 2 πr^2=a^2 πr2=a2,推出 a = r π a=r\sqrtπ a=rπ
圆周长= 2 π r 2πr 2πr,正方形周长= 4 r π 4r\sqrtπ 4rπ
2 π r 4 r π = π 2 π \frac{2πr}{4r\sqrtπ}=\frac{π}{2\sqrtπ} 4rπ2πr=2ππ
可以推出 π < 4 π π<\sqrt{4π} π<4π,正方形的周长更长
答案C
【例题12】如图所示,某个圆柱形的管子如下放置在水平地面上,管子直径为1m,则现在要做一个棚子遮住这三个管子,问棚子最低要建多高().
解题:
【例题13】圆柱体积是正方体积的 4 π 倍 \frac{4}{π}倍 π4倍().
(1)圆柱的高与正方体的高相等.
(2)圆柱的侧面积与正方体的侧面积相等.
解题:
条件(1)圆柱的高和正方体高相等,但圆柱底面积不确定,条件不充分。
条件(2)圆柱的侧面积和正方体侧面积相等,但圆柱高不确定,条件不充分。
两条件都不充分,联合考虑,答案C或E
联合条件(1)高相等,将圆柱和正方体高均设为1
联合条件(2)侧面积相等 { 圆柱体侧面积: 2 π r ∗ 1 正方体侧面积: 4 ∗ 1 2 \begin{cases} 圆柱体侧面积:2πr*1\\ 正方体侧面积:4*1^2\\ \end{cases} {圆柱体侧面积:2πr∗1正方体侧面积:4∗12→ { 2 π r = 4 r = 2 π \begin{cases} 2πr=4\\ r=\frac{2}{π}\\ \end{cases} {2πr=4r=π2
那么 V 圆柱 V 正方体 = π ( 2 π ) 2 ∗ 1 1 3 = 4 π \frac{V_{圆柱}}{V_{正方体}}=\frac{π(\frac{2}{π})^2*1}{1^3}=\frac{4}{π} V正方体V圆柱=13π(π2)2∗1=π4
答案C
【例题14】两个球形容器,若将大球中溶液的 2 5 \frac{2}{5} 52倒入小球中,正好可装满小球,那么大球与小球的半径之比等于().
A.5:3
B.8:3
C. 3 5 : 3 2 ^3\sqrt5:^3\sqrt2 35:32
D. 3 2 0 : 3 5 ^3\sqrt20:^3\sqrt5 320:35
E.以上均不正确
解题:
设大球半径 R , 小球半径 r 设大球半径R,小球半径r 设大球半径R,小球半径r
球体积 = 4 3 π r 3 球体积=\frac{4}{3}πr^3 球体积=34πr3
V 大球 V 小球 = R 3 r 3 = 5 2 \frac{V_{大球}}{V_{小球}}=\frac{R^3}{r^3}=\frac{5}{2} V小球V大球=r3R3=25
那么 R r = 3 5 3 2 那么\frac{R}{r}=\frac{^3\sqrt5}{^3\sqrt2} 那么rR=3235
答案C
【例题15】三个球中,最大球的体积是另外两个球体积和的三倍().
(1)三个球的半径比为1:2:3.
(2)大球的半径是另外两个球的半径之和.
解题:
条件(1)将三个球的半径按照比例设为 1 、 2 、 3 1、2、3 1、2、3则有 3 3 = 3 ( 1 3 + 2 3 ) 3^3=3(1^3+2^3) 33=3(13+23)条件充分。
条件(2)大球半径=小球1半径+小球2半径,用极端法考虑
假设小球1半径无线接近大球半径则最大球体积和球1的体积无线相近,条件2不充分
答案A
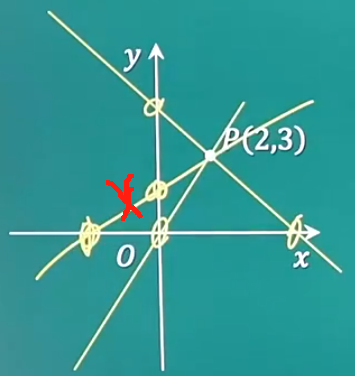
【例题16】过点 P ( 2.3 ) P(2.3) P(2.3)且在 x x x轴和 y y y轴上的截距相等至直线有()条.
A.1
B.2
C.3
D.4
E.无数
解题:
截距带正负符号的,所以只有2条
答案B
【例题17】已知 3 3 3个点作别分别为 A ( 3 , − 4 ) 、 B ( − 3 , 2 ) A(3,-4)、B(-3,2) A(3,−4)、B(−3,2)和 C ( 1 , 2 ) C(1,2) C(1,2),则点 C C C到 A B AB AB所在直线的距离.()
解题:
根据点 A ( 3 , − 4 ) 、 B ( − 3 , 2 ) A(3,-4)、B(-3,2) A(3,−4)、B(−3,2)两点求直线方程
y − y 1 y 2 − y 1 = x − x 1 x 2 − x 1 \frac{y-y_1}{y_2-y_1}=\frac{x-x_1}{x_2-x_1} y2−y1y−y1=x2−x1x−x1
y + 4 2 + 4 = x − 3 − 3 − 3 \frac{y+4}{2+4}=\frac{x-3}{-3-3} 2+4y+4=−3−3x−3
− x − y − 1 = 0 ( 也可以写成 x + y + 1 = 0 ) -x-y-1=0(也可以写成x+y+1=0) −x−y−1=0(也可以写成x+y+1=0)
求 C 点到直线 − x − y − 1 = 0 的距离 d 求C点到直线-x-y-1=0的距离d 求C点到直线−x−y−1=0的距离d
d = ∣ A x 0 + B y 0 + C ∣ A 2 + B 2 = ∣ ( − 1 ∗ 1 ) + ( − 1 ∗ 2 ) + ( − 1 ) ∣ ( − 1 ) 2 + ( − 1 ) 2 = 2 2 d=\frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}=\frac{|(-1*1)+(-1*2)+(-1)|}{\sqrt{(-1)^2+(-1)^2}}=2\sqrt2 d=A2+B2∣Ax0+By0+C∣=(−1)2+(−1)2∣(−1∗1)+(−1∗2)+(−1)∣=22
【例题18】 ( m + 2 ) x + 3 m y + 1 = 0 (m+2)x+3my+1=0 (m+2)x+3my+1=0与 ( m − 2 ) x + ( m + 2 ) y − 3 = 0 (m-2)x+(m+2)y-3=0 (m−2)x+(m+2)y−3=0相互垂直().
(1) m = 1 2 m=\frac{1}{2} m=21.
(2) m = − 2 m=-2 m=−2.
解题:
条件(1) m = 1 2 m=\frac{1}{2} m=21带入公式: { 5 x + 3 y + 2 = 0 − 3 x + 5 y − 6 = 0 \begin{cases} 5x+3y+2=0\\ -3x+5y-6=0\\ \end{cases} {5x+3y+2=0−3x+5y−6=0是否垂直?
验证斜率 k 1 ∗ k 2 = − 1 或 A 1 A 2 + B 1 B 2 = 0 k1*k2=-1或A_1A_2+B_1B_2=0 k1∗k2=−1或A1A2+B1B2=0满足其中一个即可。
5 ∗ ( − 3 ) + 3 ∗ 5 = 0 5*(-3)+3*5=0 5∗(−3)+3∗5=0条件充分,两条线垂直。
条件(2) m = − 2 m=-2 m=−2带入公式: { 6 y − 1 = 0 4 x + 3 = 0 \begin{cases} 6y-1=0\\ 4x+3=0\\ \end{cases} {6y−1=04x+3=0是否垂直?
0 ∗ 4 + 6 ∗ 0 = 0 0*4+6*0=0 0∗4+6∗0=0条件充分,两条线垂直。
条件2两条线单独都是垂直直线,那么联合一定会有交点!
答案D
【例题19】已知 b > 0 b>0 b>0,直线 ( b 2 + 1 ) x + a y + 2 = 0 (b^2+1)x+ay+2=0 (b2+1)x+ay+2=0与直线 x − b 2 y − 1 = 0 x-b^2y-1=0 x−b2y−1=0互相垂直,则 a b ab ab的最小值等于().
A.1
B.2
C.4
D. 2 2 2\sqrt2 22
E. 2 3 2\sqrt3 23
解题:
两条直线垂直,用系数关系 A 1 A 2 + B 1 B 2 = 0 A_1A_2+B_1B_2=0 A1A2+B1B2=0
( b 2 + 1 ) ∗ 1 + a ∗ ( − b 2 ) = 0 (b^2+1)*1+a*(-b^2)=0 (b2+1)∗1+a∗(−b2)=0
化简得 b 2 + 1 − a b 2 = 0 b^2+1-ab^2=0 b2+1−ab2=0
a b 2 = b 2 + 1 ab^2=b^2+1 ab2=b2+1
a b = b 2 + 1 b = b + 1 b ab=\frac{b^2+1}{b}=b+\frac{1}{b} ab=bb2+1=b+b1限制为正(b>0)+求最值推出→均值定理
根据均值定理 a b = b 2 + 1 b = b + 1 b ≥ 2 b ∗ 1 b = 2 ab=\frac{b^2+1}{b}=b+\frac{1}{b}≥2\sqrt{b*\frac{1}{b}}=2 ab=bb2+1=b+b1≥2b∗b1=2
答案B
【例题20】过点A ( − 2 , m ) (-2,m) (−2,m)和 B ( m , 4 ) B(m,4) B(m,4)的直线与直线方程 2 x + y − 1 = 0 2x+y-1=0 2x+y−1=0平行.()
(1) m = − 8 m=-8 m=−8.
(2) m = 2 m=2 m=2.
解题:
两直线平行斜率关系 k 1 = k 2 k_1=k_2 k1=k2
过点A ( − 2 , m ) (-2,m) (−2,m)和 B ( m , 4 ) B(m,4) B(m,4)的直线斜率 k A B = y 2 − y 1 x 2 − x 1 = 4 − m m + 2 k_{AB}=\frac{y_2-y_1}{x_2-x_1}=\frac{4-m}{m+2} kAB=x2−x1y2−y1=m+24−m
直线 2 x + y − 1 = 0 , 则 y = − 2 x + 1 ,斜率 k = − 2 2x+y-1=0,则y=-2x+1,斜率k=-2 2x+y−1=0,则y=−2x+1,斜率k=−2
条件(1)带入公式 k A B = y 2 − y 1 x 2 − x 1 = 4 − m m + 2 = 4 + 8 − 8 + 2 = − 2 k_{AB}=\frac{y_2-y_1}{x_2-x_1}=\frac{4-m}{m+2}=\frac{4+8}{-8+2}=-2 kAB=x2−x1y2−y1=m+24−m=−8+24+8=−2,条件充分。
条件(2) k A B = 4 − 2 2 + 2 = 1 2 条件不充分 k_{AB}=\frac{4-2}{2+2}=\frac{1}{2}条件不充分 kAB=2+24−2=21条件不充分
答案A
【3.平面几何】
角度与弧度
平角: π = 180 ° π=180° π=180°
周角: 2 π = 360 ° 2π=360° 2π=360°
三角形
三角形任意两边之和大于第三边,任意两边之差小于第三边
三角形内角和180°
三角形面积
S △ = 1 2 任意一个底边 ∗ 相对应的高 S_△=\frac{1}{2}任意一个底边*相对应的高 S△=21任意一个底边∗相对应的高
直角三角形
勾股定理 a 2 + b 2 = c 2 ( c 为斜边 ) a^2+b^2=c^2(c为斜边) a2+b2=c2(c为斜边){3,4,5}、{6,8,10}、{5,12,13}
若三角形底边为圆的直径,顶点在圆周上,这是个直角三角形
直角三角形斜边中线等于斜边一半
垂线定理> A C 2 − A H 2 = B C 2 − B H 2 AC^2-AH^2=BC^2-BH^2 AC2−AH2=BC2−BH2
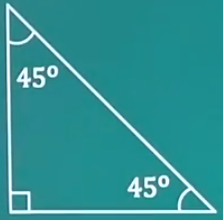
等腰直角三角形45°
三边长度之比为 1 : 1 : 2 1:1:\sqrt2 1:1:2、周长 2 + 2 2+\sqrt2 2+2、面积 1 2 \frac{1}{2} 21
三边长度之比为 2 : 2 : 2 \sqrt2:\sqrt2:2 2:2:2、周长 2 + 2 2 2+2\sqrt2 2+22、面积 1 1 1
等腰直角三角形30°
三边长度之比为 1 : 3 : 2 1:\sqrt3:2 1:3:2、充分必要条件
三边长度之比为 1 : 3 : 2 1:\sqrt3:2 1:3:2、周长 3 + 3 3+\sqrt3 3+3、面积 3 2 \frac{\sqrt3}{2} 23
三边长度之比为 1 2 : 3 2 : 1 \frac{1}{2}:\frac{\sqrt3}{2}:1 21:23:1、周长 3 + 3 2 \frac{3+\sqrt3}{2} 23+3、面积 3 8 \frac{\sqrt3}{8} 83
等腰三角形判定 { 任意两个角相等 任意两条边相等 三线中有任意两条重合(顶角平分线,底边中线,底边高) \begin{cases} 任意两个角相等\\ 任意两条边相等\\ 三线中有任意两条重合(顶角平分线,底边中线,底边高) \end{cases} ⎩ ⎨ ⎧任意两个角相等任意两条边相等三线中有任意两条重合(顶角平分线,底边中线,底边高)
等边三角形判定 { 三线合一 三条边相等 内角 60 ° 边长 : 垂线 = 1 : 3 2 边长为 a 的等边三角形,高为 3 2 a ,面积为 3 4 a 2 \begin{cases} 三线合一\\ 三条边相等\\ 内角60°\\ 边长:垂线=1:\frac{\sqrt3}{2}\\ 边长为a的等边三角形,高为\frac{\sqrt3}{2}a,面积为\frac{\sqrt3}{4}a^2 \end{cases} ⎩ ⎨ ⎧三线合一三条边相等内角60°边长:垂线=1:23边长为a的等边三角形,高为23a,面积为43a2
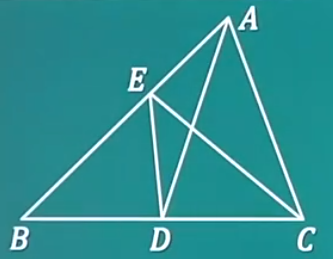
三角形 ▪ 等高模型
底同线+共顶点→等高模型
①面积比=底边比
②面积和=底边和 x 高
底同线+共顶点→等高模型
无论P点如何运动,分割出的三角形都是正方形的一半。
无论P点如何运动,分割出的三角形都是平行四边形的一半。
四边形 ▪ 菱形 { 四条边相等 对角相等 邻角互补,邻角和 = 180 ° 面积 = 对角线 ∗ 对角线 2 \begin{cases} 四条边相等\\ 对角相等\\ 邻角互补,邻角和=180°\\ 面积=\frac{对角线*对角线}{2}\\ \end{cases} ⎩ ⎨ ⎧四条边相等对角相等邻角互补,邻角和=180°面积=2对角线∗对角线
对角线互相垂直的任意四边形,面积都等于对角线之积的一半
四边形 ▪ 梯形
只有一组对边平行,另一组对边不平行的四边形叫做梯形
梯形面积= (上底 + 下底) ∗ 高 2 \frac{(上底+下底)*高}{2} 2(上底+下底)∗高
等腰梯形,两底角相等
圆与扇形
圆面积: S = π r 2 S=πr^2 S=πr2
圆周长: L = 2 π r L=2πr L=2πr
扇形面积 S = 圆心角 2 π π r 2 S=\frac{圆心角}{2π}πr^2 S=2π圆心角πr2(π=180°)
弧长: L = 圆心角 2 π 2 π r L=\frac{圆心角}{2π}2πr L=2π圆心角2πr
同一段弧所对的圆周角是圆心角的一半
直径所对的圆周角是直角
垂径定理:垂直于弦的直径平均这条弦以及弦所对应的两条弧
圆内接四边形对角互补 ( 180 ° ) (180°) (180°)
圆内接四边形对应三角形相似
【4.立体几何】
立方体
柱体
柱体体积=底面积 x 高
圆柱
圆柱体积 = π r 2 ∗ h =πr^2*h =πr2∗h
圆柱侧面积 = 2 π r h =2πrh =2πrh
圆柱全表面积 = 2 π r 2 + 2 π r h =2πr^2+2πrh =2πr2+2πrh
球体
球体积 V = 4 3 π R 3 V=\frac{4}{3}πR^3 V=34πR3
球表面积 S = 4 π R 2 S=4πR^2 S=4πR2
【5.平面解析几何】
直线
圆
抛物线
点和直线
两点中点坐标 = x 1 + x 2 2 , y 1 + y 2 2 =\frac{x_1+x_2}{2},\frac{y_1+y_2}{2} =2x1+x2,2y1+y2
两点间的距离公式 A B = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 AB=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2} AB=(x2−x1)2+(y2−y1)2
点和直线 ▪ 直线基础
平面上两点可以确定一条直线
一般式直线方程
①任意二元一次方程 A x + B y + C = 0 ( A , B 不同时为零, A 2 + B 2 ≠ 0 ) ,呈现一条直线 . 一般会写成 y = x + 1 ①任意二元一次方程Ax+By+C=0(A,B不同时为零,A^2+B^2≠0),呈现一条直线.一般会写成y=x+1 ①任意二元一次方程Ax+By+C=0(A,B不同时为零,A2+B2=0),呈现一条直线.一般会写成y=x+1
②当 x 或 y 一方为 0 时,此时为一条横向或纵向垂直的线 . ②当x或y一方为0时,此时为一条横向或纵向垂直的线. ②当x或y一方为0时,此时为一条横向或纵向垂直的线.
两点式直线方程
y − y 1 y 2 − y 1 = x − x 1 x 2 − x 1 其中( x 1 ≠ x 2 ) \frac{y-y_1}{y_2-y_1}=\frac{x-x_1}{x_2-x_1}其中(x_1≠x_2) y2−y1y−y1=x2−x1x−x1其中(x1=x2)
截距式直线方程
在 x 轴截距为 a ,在 y 轴截距为 b 在x轴截距为a,在y轴截距为b 在x轴截距为a,在y轴截距为b
x a + y b = 1 ( 其中 a ≠ 0 , b ≠ 0 ) \frac{x}{a}+\frac{y}{b}=1(其中a≠0,b≠0) ax+by=1(其中a=0,b=0)
点斜式直线方程
经过点 P ( x 0 , y 0 ) , 斜率为 k 的直线方程 P(x_0,y_0),斜率为k的直线方程 P(x0,y0),斜率为k的直线方程
y − y 0 = k ( x − x 0 ) y-y_0=k(x-x_0) y−y0=k(x−x0)
斜截式直线方程
在 y 轴截距为 b ,斜率为 k 的直线方程 在y轴截距为b,斜率为k的直线方程 在y轴截距为b,斜率为k的直线方程
y = k x + b y=kx+b y=kx+b
斜率 k k k(正切tan)
两点斜率公式
过两点 P 1 ( x 1 , y 1 ) , P 2 ( x 2 , y 2 ) 的直线斜率 k ( 正切 t a n ) P_1(x_1,y_1),P_2(x_2,y_2)的直线斜率k(正切tan) P1(x1,y1),P2(x2,y2)的直线斜率k(正切tan)
k = y 2 − y 1 x 2 − x 1 , x 1 ≠ x 2 k=\frac{y_2-y_1}{x_2-x_1},x_1≠x_2 k=x2−x1y2−y1,x1=x2
点到直线距离公式
点 P ( x 0 , y 0 ) 到直线 A x + B x + C = 0 的距离 d = ∣ A x 0 + B y 0 + C ∣ A 2 + B 2 P(x_0,y_0)到直线Ax+Bx+C=0的距离d=\frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}} P(x0,y0)到直线Ax+Bx+C=0的距离d=A2+B2∣Ax0+By0+C∣
两直线关系
两线相交
交点个数:联立方程,有唯1解,交点坐标 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)
斜率关系:垂直时 k 1 ∗ k 2 = − 1 ( k 1 ≠ k 2 ) k1*k2=-1(k1≠k2) k1∗k2=−1(k1=k2)
系数关系:垂直时 A 1 A 2 + B 1 B 2 = 0 ( A 1 B 2 ≠ A 2 B 1 ) A_1A_2+B_1B_2=0(A_1B_2≠A_2B_1) A1A2+B1B2=0(A1B2=A2B1)
两线平行
交点个数:无解
斜率关系: k 1 = k 2 k1=k2 k1=k2
系数关系: A 1 A 2 = B 1 B 2 ≠ C 1 C 2 \frac{A_1}{A_2}=\frac{B_1}{B_2}≠\frac{C_1}{C_2} A2A1=B2B1=C2C1
两平行直线间距离公式: d = ∣ C 1 − C 2 ∣ A 2 + B 2 d=\frac{|C_1-C_2|}{\sqrt{}{A^2+B^2}} d=A2+B2∣C1−C2∣
两线重合
交点个数:2个以上,联立方程有无数个解
斜率关系: k 1 = k 2 k1=k2 k1=k2
系数关系: A 1 B 2 = A 2 B 1 、 B 1 C 2 = B 2 C 1 A_1B_2=A_2B_1、B_1C_2=B_2C_1 A1B2=A2B1、B1C2=B2C1
解析几何 · 圆
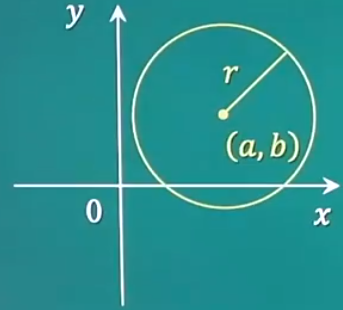
圆的标准方程 ( x − a ) 2 + ( y − b ) 2 = r 2 (半径) (x-a)^2+(y-b)^2=r^2(半径) (x−a)2+(y−b)2=r2(半径)
【举例1】 ( x − 2 ) 2 + ( y − 1 ) 2 = 4 可知圆心坐标( 2 , 1 )半径 2 (x-2)^2+(y-1)^2=4可知圆心坐标(2,1)半径2 (x−2)2+(y−1)2=4可知圆心坐标(2,1)半径2
【举例2】 ( x + 2 ) 2 + ( y − 1 ) 2 = 4 可知圆心坐标( − 2 , 1 )半径 2 (x+2)^2+(y-1)^2=4可知圆心坐标(-2,1)半径2 (x+2)2+(y−1)2=4可知圆心坐标(−2,1)半径2
当圆心在原点 ( 0 , 0 ) (0,0) (0,0)时,圆的方程为 x 2 + y 2 = r 2 x^2+y^2=r^2 x2+y2=r2
【单位圆】 x 2 + y 2 = 1 x^2+y^2=1 x2+y2=1(半径为1)
圆的一般方程 x 2 + y 2 + D x + E y + F = 0 x^2+y^2+Dx+Ey+F=0 x2+y2+Dx+Ey+F=0其中满足 D 2 + E 2 − 4 F > 0 D^2+E^2-4F>0 D2+E2−4F>0
①: x 2 + y 2 + D x + E y + F = 0 x^2+y^2+Dx+Ey+F=0 x2+y2+Dx+Ey+F=0.(当 F = 0 F=0 F=0时,圆过原点)
②: ( x 2 + D x ) + ( y 2 + E y ) + F = 0 (x^2+Dx)+(y^2+Ey)+F=0 (x2+Dx)+(y2+Ey)+F=0.
③: x 2 + D x + ( D 2 ) 2 + y 2 + E y + ( E 2 ) 2 + F − ( D 2 ) 2 − ( E 2 ) 2 = 0 x^2+Dx+(\frac{D}{2})^2+y^2+Ey+(\frac{E}{2})^2+F-(\frac{D}{2})^2-(\frac{E}{2})^2=0 x2+Dx+(2D)2+y2+Ey+(2E)2+F−(2D)2−(2E)2=0 .
④: ( x + D 2 ) 2 + ( y + E 2 ) 2 = D 2 + E 2 − 4 F 4 (x+\frac{D}{2})^2+(y+\frac{E}{2})^2=\frac{D^2+E^2-4F}{4} (x+2D)2+(y+2E)2=4D2+E2−4F.
⑤:圆的半径 r = D 2 + E 2 − 4 F 4 r=\sqrt{\frac{D^2+E^2-4F}{4}} r=4D2+E2−4F
若坐标平面上有一点满足圆方程,则这一点在此圆上。
















































































 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










