Ford-Fulkerson算法求最大流Java实现

在最大流问题中，我们希望在不违反任何容量限制的情况下，计算出从源结点到汇点的最大流速。对于流网络中的每一个结点，遵守“流量守恒”：除了源结点与汇点之外，流入该结点的速率等于流出该结点的速率。

《算法导论》书中所给出的伪代码如下所示：

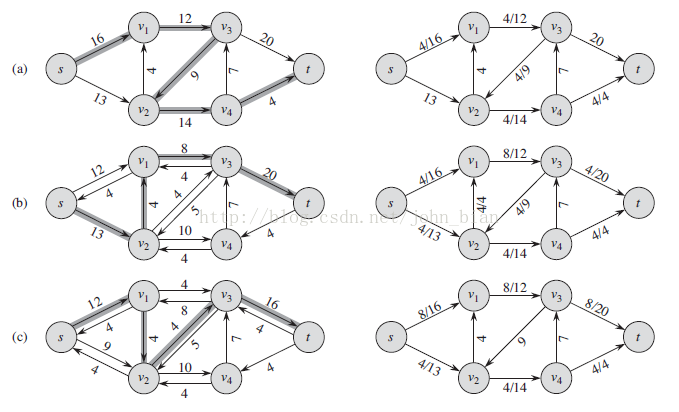
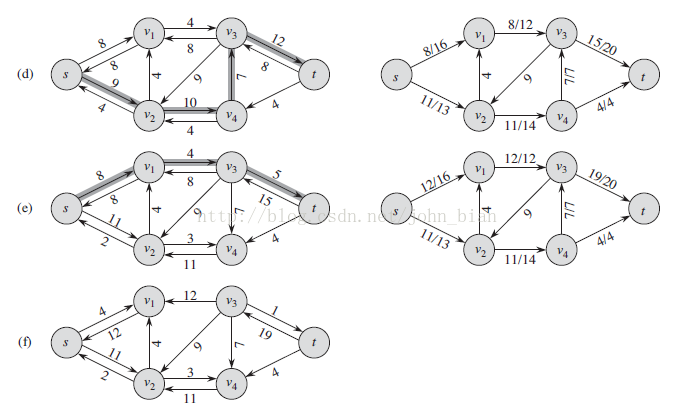
下面是一个求最大流的过程

下面是用Java的代码实现：

package Ford_Fulkerson;
/**
 * 网络中的边
 * @author sdu20
 *
 */
public class Edge {

	private int v1;
	private int v2;
	private int capacity;
	private int flow;
	
	public Edge(int v1,int v2,int flow,int capacity){
		this.v1 = v1;
		this.v2 = v2;
		this.capacity = capacity;
		this.flow = flow;
	}
	
	public int getV1(){
		return v1;
	}
	
	public int getV2(){
		return v2;
	}
	
	public int getCapacity(){
		return capacity;
	}
	
	public int getFlow(){
		return flow;
	}
	
	public void setFlow(int f){
		flow = f;
	}
}

package Ford_Fulkerson;
/**
 * 残存网络中的边
 * @author sdu20
 *
 */
public class Edge2 {
	private int v1;
	private int v2;
	private int flow;
	
	public Edge2(int v1,int v2,int flow){
		this.v1 = v1;
		this.v2 = v2;
		this.flow = flow;
	}
	
	public int getV1(){
		return v1;
	}
	
	public int getV2(){
		return v2;
	}
	
	public int getFlow(){
		return flow;
	}
	
	public void setFlow(int f){
		flow = f;
	}

}

package Ford_Fulkerson;
import java.util.*;
/**
 * 残存网络Gf
 * @author sdu20
 *
 */
public class Gf {

	private int vNum;
	private int eNum;
	private LinkedList<Edge2>[] GLists;
	
	public Gf(int n){
		vNum = n;
		eNum = 0;
		GLists = new LinkedList[n];
		
		for(int i = 0;i<n;i++)
			GLists[i] = new LinkedList<>();
	}
	
	public void insertEdge(Edge2 e){
		int v1 = e.getV1();
		GLists[v1].add(e);
		eNum++;
	}
	
	/**
	 * 返回一条增广路径
	 * @return
	 */
	public LinkedList<Integer> augmentingPath(){
		
		LinkedList<Integer> list = new LinkedList<>();
		Queue<Integer> queue = new LinkedList<>();
		int[] reached = new int[vNum];
		int[] preNode = new int[vNum];
		for(int i = 0;i<vNum;i++){
			reached[i] = 0;
			preNode[i] = -1;
		}
		preNode[0] = -1;
		
		reached[0] = 1;
		queue.add(0);
		while(!queue.isEmpty()){//没有循环起来
			int now = queue.poll();
			
			LinkedList<Edge2> inlist = (LinkedList<Edge2>) GLists[now].clone();
			
			while(!inlist.isEmpty()){
				
				Edge2 e = inlist.pop();
				int v2 = e.getV2();
				
				if(reached[v2]==0){
					queue.add(v2);
					reached[v2] = 1;
					preNode[v2] = now;
				}
			}
		}
		
		for(int i = 0;i<vNum;i++){
			System.out.println(reached[i]+"     "+preNode[i]);
		}
		
		if(reached[vNum-1]==0){
			//System.out.println("here");
			return list;
			
		}
		
		int pointnum = vNum-1;
		while(pointnum!=-1){
			list.add(0, pointnum);
			pointnum = preNode[pointnum];
		}
				
		return list;
	} 
	
	/**
	 * 根据增广路径得到需要调整的值
	 * @param list
	 * @return
	 */
	public int changeNum(LinkedList<Integer> list){
		if(list.equals(null))
			return 0;
		int minchange = 1000;
		int v1 = 0;
		for(int i = 1;i<list.size();i++){
			int v2 = list.get(i);
			LinkedList<Edge2> elist = (LinkedList<Edge2>) GLists[v1].clone();
			Edge2 edge = elist.pop();
			while(edge.getV2()!=v2){
				edge = elist.pop();
			}
			if(minchange>edge.getFlow())
				minchange = edge.getFlow();
			
			v1 = v2;
		}
		
		return minchange;
	}
	
	public void bianli(){
		System.out.println("残存网络 共 "+vNum+" 个顶点， "+eNum+" 条边");
		for(int i = 0;i<vNum;i++){
			if(GLists[i].size()==0){
				System.out.println(i+"没有后继");
				continue;
			}
			for(int j = 0;j<GLists[i].size();j++){
				Edge2 e = GLists[i].get(j);
				System.out.println("[ "+e.getV1()+" , "+e.getV2()+" , "+e.getFlow()+" ]");
			}
		}
	}
}

package Ford_Fulkerson;
import java.util.*;
/**
 * 流网络
 * @author sdu20
 *
 */
public class Graph {
	
	private int vNum;
	private int eNum;
	private Gf gf;
	private LinkedList<Edge>[] GLists;
	
	public Graph(int n){
		vNum = n;
		eNum = 0;
		GLists = new LinkedList[n];
		
		for(int i = 0;i<n;i++)
			GLists[i] = new LinkedList<>();
	}
	
	public void insertEdge(Edge e){
		int v1 = e.getV1();
		GLists[v1].add(e);
		eNum++;
	}
	
//	public void deleteEdge(Edge e){
//		int v1 = e.getV1();
//		int v2 = e.getV1();
//		
//	}
	
	public void produceGf(){
		gf = new Gf(vNum);
		
		for(int i = 0;i<vNum;i++){
			LinkedList<Edge> list = (LinkedList<Edge>) GLists[i].clone();
			
			while(!list.isEmpty()){
				
				Edge edge = list.pop();
				int v1 = edge.getV1();
				int v2 = edge.getV2();
				int flow = edge.getFlow();
				int capacity = edge.getCapacity();
				
				if(flow==0){
					gf.insertEdge(new Edge2(v1,v2,capacity));
				}else{
					if(flow==capacity){
						gf.insertEdge(new Edge2(v2,v1,capacity));
					}else if(flow<capacity){
						gf.insertEdge(new Edge2(v1,v2,capacity-flow));
						gf.insertEdge(new Edge2(v2,v1,flow));
					}
				}
			}
		}
	}
	
	public Gf getGf(){
		return gf;
	}
	
	private LinkedList<Integer> augmentingPath(){
		return gf.augmentingPath();
	}
	
	private int changeNum(LinkedList<Integer> list){
		return gf.changeNum(list);
	}
	
	/**
	 * 最大流
	 */
	public void MaxFlow(){
		produceGf();
		gf.bianli();
		LinkedList<Integer> list = augmentingPath();
		
		while(list.size()>0){
			
			int changenum = changeNum(list);
			
			LinkedList<Integer> copylist = (LinkedList<Integer>) list.clone();//调试
			System.out.println("list:");
			while(!copylist.isEmpty()){
				System.out.print(copylist.pop()+"  ");
			}
			System.out.println();
			System.out.println("changenum: "+changenum);
					
			int v1 = 0;
			for(int i = 1;i<list.size();i++){
				int v2 = list.get(i);
				if(!GLists[v1].isEmpty()){
					int j = 0;
					Edge e = GLists[v1].get(j);
					while(e.getV2()!=v2 && j<GLists[v1].size()){
						e = GLists[v1].get(j);
						j++;						
					}
					if(e.getV2()!=v2 && j==GLists[v1].size()){//调试
						j = 0;
						e = GLists[v2].get(j);
						while(e.getV2()!=v1 && j<GLists[v2].size()){
							e = GLists[v2].get(j);
							j++;
						}
						
					}
					e.setFlow(e.getFlow()+changenum);
				}
				v1  = v2;
				
			}
			bianli();	
			produceGf();
			gf.bianli();
			list = augmentingPath();
		}
	}
	
	public void bianli(){
		System.out.println("共有 "+vNum+" 个顶点， "+eNum+" 条边");
		for(int i = 0;i<vNum;i++){
			if(GLists[i].size()==0)
				continue;
			for(int j = 0;j<GLists[i].size();j++){
				Edge e = GLists[i].get(j);
				System.out.println("[ "+e.getV1()+" , "+e.getV2()+" , "+e.getFlow()+" , "+e.getCapacity()+" ]");
			}
		}
	}
	
	public void showResult(){
		bianli();
		int maxflow = 0;
		
		for(int i = 0;i<vNum;i++){
			if(GLists[i].size()>0){
				for(int j = 0;j<GLists[i].size();j++){
					if(GLists[i].get(j).getV2() == vNum-1){
						maxflow += GLists[i].get(j).getFlow();
					}
				}
			}
		}
		System.out.println("最大流为 "+maxflow);
			
	}

}

package Ford_Fulkerson;

public class Main {

	public static void main(String[] args){		
		test();
	}
	
	private static void test(){
		Graph graph = new Graph(6);
		Edge[] edges = new Edge[9];
		
		edges[0] = new Edge(0,1,0,16);
		edges[1] = new Edge(0,2,0,13);
		edges[2] = new Edge(1,3,0,12);
		edges[3] = new Edge(2,1,0,4);
		edges[4] = new Edge(2,4,0,14);
		edges[5] = new Edge(3,2,0,9);
		edges[6] = new Edge(3,5,0,20);
		edges[7] = new Edge(4,3,0,7);
		edges[8] = new Edge(4,5,0,4);
		
		for(int i = 0;i<9;i++)
			graph.insertEdge(edges[i]);
		
		graph.MaxFlow();
		graph.showResult();
	}
	
	public static void test2(){
		Graph graph = new Graph(6);
		
		Edge[] edges = new Edge[9];
		edges[0] = new Edge(0,1,4,16);
		edges[1] = new Edge(0,2,0,13);
		edges[2] = new Edge(1,3,4,12);
		edges[3] = new Edge(2,1,0,4);
		edges[4] = new Edge(2,4,4,14);
		edges[5] = new Edge(3,2,4,9);
		edges[6] = new Edge(3,5,0,20);
		edges[7] = new Edge(4,3,0,7);
		edges[8] = new Edge(4,5,4,4);
		
		for(int i = 0;i<9;i++)
			graph.insertEdge(edges[i]);
		
		graph.bianli();
		
		graph.MaxFlow();
		graph.bianli();
	}
}

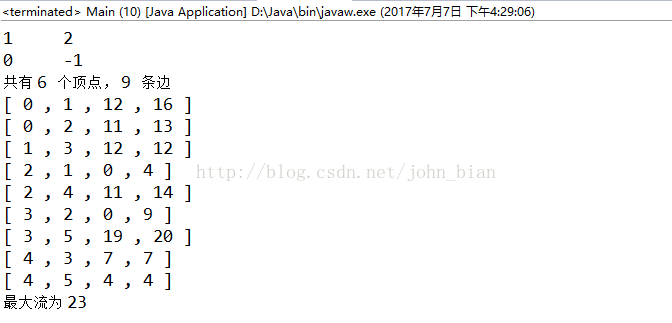
运行截图如下