浅析树状数组

原名Fenwick Tree/Binary Index Tree

存在的必要

最好不要以线段树的区间思维来理解树状数组，树状数组的前提是满足区间减法，即求的是所谓的“前缀和”（其实都是[1,x]的区间）

树状数组能做的,线段树都能做,而且学上来线段树比他简单许多
但树状数组的时空复杂度相对于线段树都优了许多,看下面这张对比图

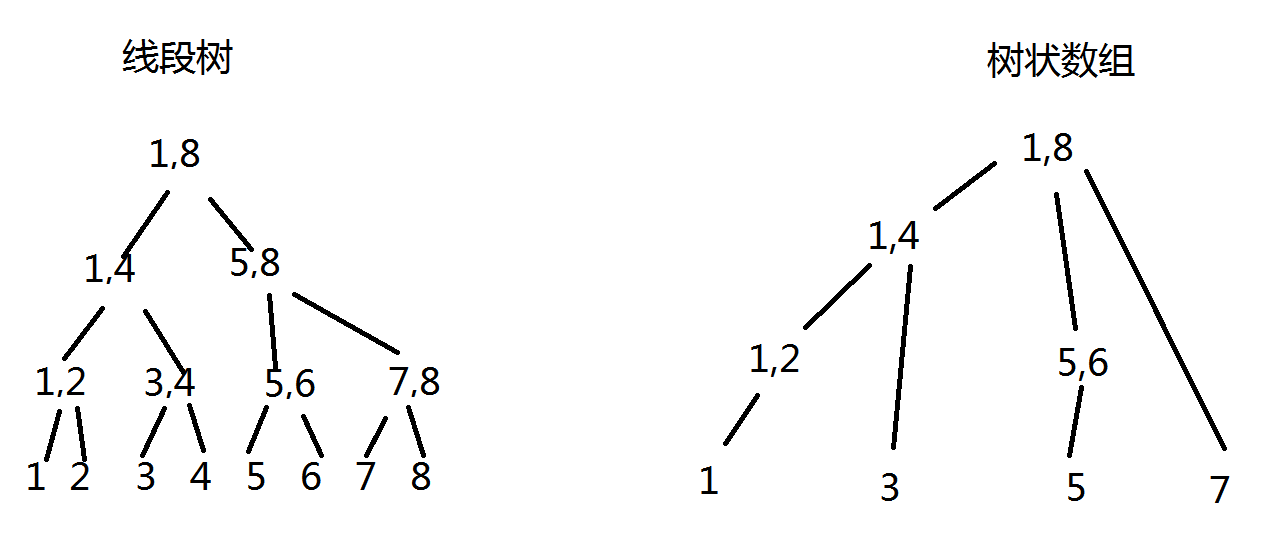
一个显然的结论 节点数从2n减少至n, 这样一来,虽然说其操作复杂度与线段树同为log n,但常数却差别很大,大数据通常都是上百ms的差距 而且树状数组10行能解决的事情,线段树要30行

线段树的常数究竟大在哪里呢?
点多 （废话）
基于二分实现访问(虽然是Log),速度较慢

基本结构

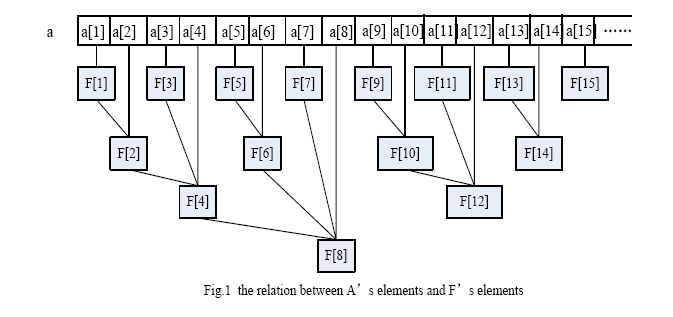
第一层是原序列,第二层开始是树状数组的叶子节点

先看看从这个图中能发现什么
1.最大的差别是,节点fi直接存了自己的ai, 这也是他减少冗余的原因之一吧
2.fi父亲节点都不超过i*2
3.奇数fi都在第一层,这个又有什么含义呢?

点3是最重要的
奇偶要从二进制说起
当二进制第一位为1时,那么该数为奇数,反之为偶数
那我们将注意力转到二进制上

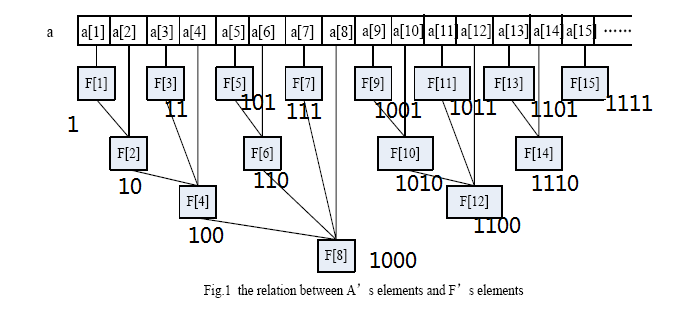
发现没有 他所在的层数是由他结尾0决定的
我觉得，这就是树状数组的核心思想,用结尾0决定位置,做到O(1)询问其父节点与区间相邻的点

而且2的结尾0个数次方就是其向前包含的数的个数,这是一个很常用的性质
写成数学形式就是

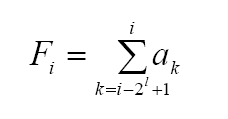
l=i的结尾0个数
不难发现,$2^l$其实i是只保留从低位到高位第一个1后的值,即所谓的lowbit()
即$2^l$=lowbit(x)=x and (-x)
在计算机中负数存的是他的补码,所以这样能保留低位1 这个自己bing一下

操作

最基本的三种操作: 建树,修改与查询

简单解释一下原理
其实建树就是修改 , 所以并为讨论

Change&Build

假设现在维护sum,我们修改节点ai的值(其实就等价于减少或增加)
结合一下前面的图,不难发现只对$F_i$和他的父亲节点有影响
设他影响的点为$F_{p1},F_{p2},F_{p3}....F_{pk}$
保证$0<p1<...<pn$
显然$p1=i$,然后我们观察一下子节点son与父节点fa的二进制,其实满足这样一组关系 :

设fa与son为其对应的二进制,记Li为二进制i结尾的0个数
我们根据性质已知$Lson+1=Lfa$
根据其思想,son的父亲节点就是求最小(在树状数组中son的位置之后的最近的fa)的fa使得$Lson+1=Lfa$
那我们就让他加一个0,如何加0呢? 不就是加上lowbit让他进位吗?
数学形式即为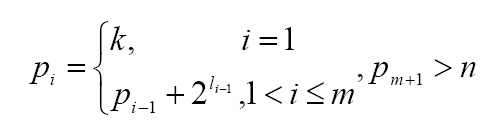
这样我们就实现了O(1)求父亲节点,然后就像这样迭代上去就完成了修改操作

void change(int loc , int v) {
      while(loc <= n) {            
          f[loc] += v;           
          loc += Lowbit(loc);     
      } 
 }

相比线段树果然短了许多吧?

查询

假如我们要求l~r的和,我们为了方便分开求1~l-1与1~r
也就是现在要求$\sum{a1..i}$
上面说了如何O(1)找父节点,这里说如何O(1)找对于区间相邻的节点
现在回头看看前面的性质

而且2的结尾0个数次方就是其向前包含的数的个数,这是一个很常用的性质

这个性质为我们求相邻节点提供了方法
我们将当前数x加入结果,然后向后找第一个他未包含的数,即$x-Lowbit(x)$,重复上述步骤
这样求出来所有i=>i’都是相邻的,而且相加得所求区间整体

int sum(int i) {     
    int sum = 0;     
    while(i > 0)     { 
        sum += f[i];
        i   -= Lowbit(i);
    }      
    return sum; 
} 

样例代码

#include <iostream>
using namespace std;
int ft[100010],a[100010];
int n,m;
int lowbit(int x) {
    return x&-x;
}
void change(int loc,int value) {
    while (loc<=n) {
        ft[loc]+=value;
        loc+=lowbit(loc);
    }
}
int sum(int x) {
    int rs=0;
    while (x>0) {
        rs+=ft[x];
        x-=lowbit(x);
    }
    return rs;
}
int query(int l,int r) {
    return sum(r)-sum(l-1);
}
int main() {
    freopen("bit.in","r",stdin);
    cin>>n;
    for (int i=1; i<=n; i++) {
        scanf("%d\n",&a[i]);
        change(i,a[i]);
    }
    cin>>m;
    scanf("\n");
    char ch;
    int a2,b;
    for (int i=0; i<m; i++) {
        ch = getchar();
        scanf("%d %d\n",&a2,&b);
        if (ch=='Q') {
            printf("%d\n",query(a2,b));
        } else {
            change(a2,b-a[a2]);
            a[a2]=b;
        }
    }
}

树状数组区间修改

用单点修改与数学方法扩展出来的区间修改，功能只有类似区间加减这种的。
首先我们有原序列A,然后我们将该序列差分为序列D，d[i]=a[i]-a[i-1]。
（当然你也可以理解为sum[i]..sum[n]的”共同增量”）
那么
$a[i]=\sum_{j=1}^{i} d[j]$
那么
$\sum a[i]=\sum\sum_{j=1}^{i} d[j]$
拆分一下，
$\sum_{i=1}^{k} a[i]$
$=\sum_{j=1}^{i} d[j]*(k-j+1)$
$=\sum_{j=1}^{i} (k+1)*d[j]-d[j]*j$
多维护d[j]*j即可.
相当于我们现在要维护两颗树状数组。

那么我们每一次修改区间[l,r],只需要修改点l与点r的相关值就可以了。