Reading Note: Progressive Growing of GANs for Improved Quality, Stability, and Variation

TITLE: Progressive Growing of GANs for Improved Quality, Stability, and Variation

AUTHOR: Tero Karras, Timo Aila, Samuli Laine, Jaakko Lehtinen

ASSOCIATION: NVIDIA

FROM: ICLR2018

CONTRIBUTION

A training methodology is proposed for GANs which starts with low-resolution images, and then progressively increases the resolution by adding layers to the networks. This incremental nature allows the training to first discover large-scale structure of the image distribution and then shift attention to increasingly finer scale detail, instead of having to learn
all scales simultaneously.

METHOD

PROGRESSIVE GROWING OF GANS

The following figure illustrates the training procedure of this work.

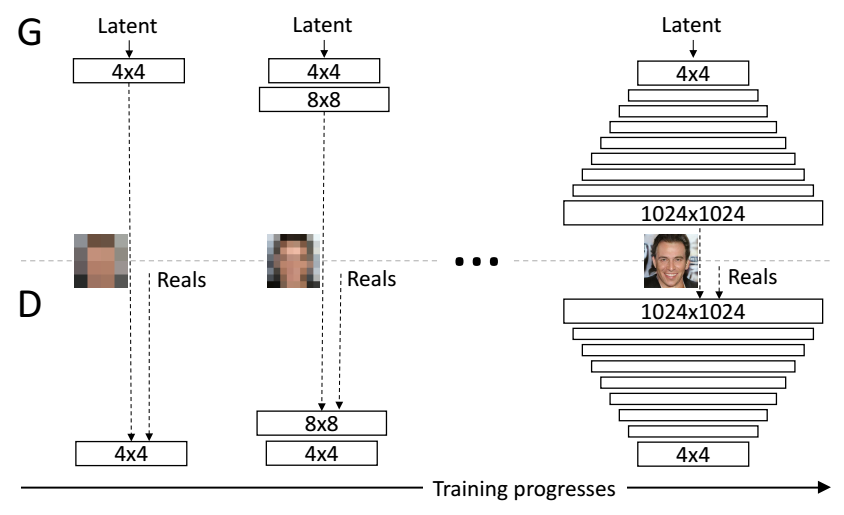
The training starts with both the generator $G$ and discriminator $D$ having a low spatial resolution of $4 \times 4$ pixels. As the training advances, successive layers are incrementally added to $G$ and $D$, thus increasing the spatial resolution of the generated images. All existing layers remain trainable throughout the process. Here $N \times N$ refers to convolutional layers operating on $N \times N$ spatial resolution. This allows stable synthesis in high resolutions and also speeds up training considerably.

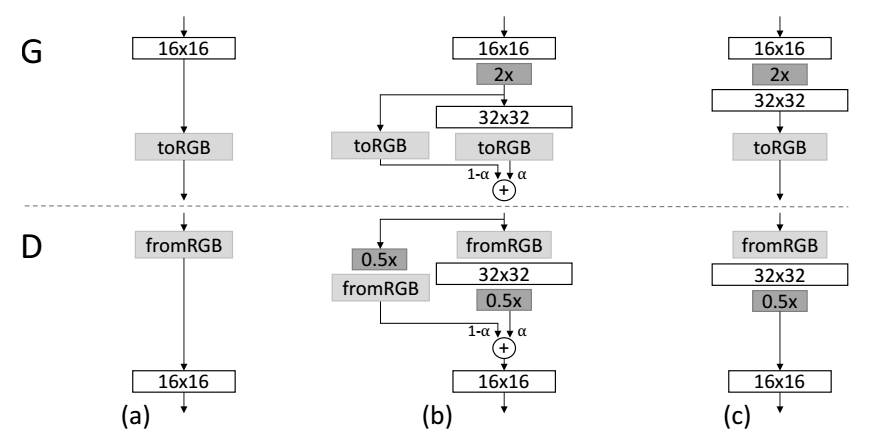
fade in is adopted when the new layers are added to double resolution of the generator $G$ and discriminator $D$ smoothly. This example illustrates the transition from $16 \times 16$ images (a) to $32 \times 32$ images (c). During the transition (b) the layers that operate on the higher resolution works like a residual block, whose weight $\alpha$ increases linearly from 0 to 1. Here 2x and 0.5x refer to doubling and halving the image resolution using nearest neighbor filtering and average pooling, respectively. The toRGB represents a layer that projects feature vectors to RGB colors and fromRGB does the reverse; both use $1 \times 1$ convolutions. When training the discriminator, the real images are downscaled to match the current resolution of the network. During a resolution transition, interpolation is carried out between two resolutions of the real images, similarly to how the generator output combines two resolutions.

INCREASING VARIATION USING MINIBATCH STANDARD DEVIATION

1. Compute the standard deviation for each feature in each spatial location over the minibatch.
2. Average these estimates over all features and spatial locations to arrive at a single value.
3. Consturct one additional (constant) feature map by replicating the value and concatenate it to all spatial locations and over the minibatch

NORMALIZATION IN GENERATOR AND DISCRIMINATOR

EQUALIZED LEARNING RATE. A trivial $N (0; 1)$ initialization is used and then explicitly the weights are scaled at runtime. To be precise, $\hat{w}_i = w_i/c$, where $w_i$ are the weights and $c$ is the per-layer normalization constant from He’s initializer.The benefit of doing this dynamically instead of during initialization is somewhat subtle, and relates to the scale-invariance in commonly used adaptive stochastic gradient descent methods.

PIXELWISE FEATURE VECTOR NORMALIZATION IN GENERATOR. To disallow the scenario where the magnitudes in the generator and discriminator spiral out of control as a result of competition, the feature vector is normalized in each pixel to unit length in the generator after each convolutional layer, using a variant of “local response normalization”, configured as

$$b_{x,y}=a_{x,y}/ \sqrt{\frac{1}{N} \sum_{j=0}^{N-1}(a_{x,y}^j)^2 + \epsilon}$$

where $\epsilon=10^{-8}$, $N$ is the number of feature maps, and $a_{x,y}$ is original feature vector, $b_{x,y}$ is the normalized feature vector in pixel $(x,y)$.