PCA降维,SVD分解和LDA
PCA(主成分分析)
在机器学习中,每一种性质代表一个特征,这样的话就很容易出现维数灾难现象。这时候我们就会用到降维的技术。
先讲一下基础的PCA降维吧。
PCA降维用一句话来说就是把原来高维的点投影到低维的区域。(至于图片自己YY吧,我就懒得找了)
那么该怎么做呢?
其实我们日常的直角坐标系不就是PCA降维的特例呢,不过是我们初中老师教的时候只告诉你记住就行,所以你也没想他是怎么来的。
见下图(A向量投影到B向量上)。那么数学公式怎么表达呢?
A
=
(
x
1
,
y
1
)
,
B
=
(
x
2
,
y
2
)
A
⋅
B
=
∣
A
∣
∣
B
∣
cos
(
α
)
A=\left(x_{1}, y_{1}\right), \quad B=\left(x_{2}, y_{2}\right) A \cdot B=|A||B| \cos (\alpha)
A=(x1,y1),B=(x2,y2)A⋅B=∣A∣∣B∣cos(α)
也就是A,B的内积,假如B的模长是1的话,那么结果就是|A|cosα,这也可以看作是内积的一种几何解释了。

看到这里相信悟性好的同学就知道我们接下来的做法了。
没错就是找到一组跟B一样的基向量,把类似A的目标向量投影到B上面。再扩展到高维就是把N维向量投影到M维向量上。
那么什么样的基向量才是最好的呢?根据 我们直观的感受,在降维以后各个向量之间离散度最大的基向量才是最好的(因为离散度小会有一部分向量点重叠,这样的话就会丢失信息)。那么离散度怎么衡量呢?均方差或者交叉熵呗,我们以均方差为例讲解。
方差:
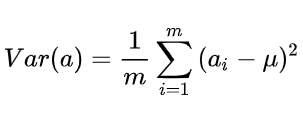
协方差(用来表示高维的离散度)
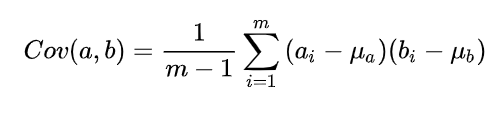
协方差矩阵
假设我们只有 a 和 b 两个变量,那么我们将它们按行组成矩阵 X:
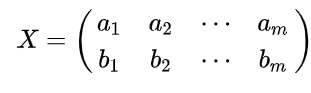
然后:
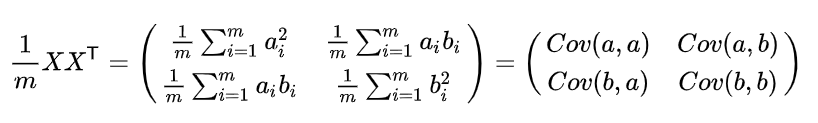
结论:
设我们有 m 个 n 维数据记录,将其排列成矩阵
X
n
,
m
X_{n, m}
Xn,m,设
C
=
1
m
X
X
T
C=\frac{1}{m} X X^{T}
C=m1XXT,则 C 是一个对称矩阵,其对角线分别对应各个变量的方差,而第 i 行 j 列和 j 行 i 列元素相同,表示 i 和 j 两个变量的协方差。
矩阵对角化
根据我们的优化条件,我们需要将除对角线外的其它元素化为 0,并且在对角线上将元素按大小从上到下排列(变量方差尽可能大),这样我们就达到了优化目的。这样说可能还不是很明晰,我们进一步看下原矩阵与基变换后矩阵协方差矩阵的关系。
设原始数据矩阵 X 对应的协方差矩阵为 C,而 P 是一组基按行组成的矩阵,设 Y=PX,则 Y 为 X 对 P 做基变换后的数据。设 Y 的协方差矩阵为 D,我们推导一下 D 与 C 的关系:
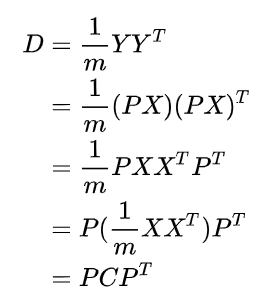
看到这里应该很熟悉,不就是特征矩阵么。我们的求解就是P矩阵也就是特征向量矩阵。
所以求解PCA的步骤是:
设有 m 条 n 维数据。
1、将原始数据按列组成 n 行 m 列矩阵 X;
2、将 X 的每一行进行零均值化,即减去这一行的均值;
3、求出协方差矩阵
C
=
1
m
X
X
⊤
C=\frac{1}{m} X X^{\top}
C=m1XX⊤;
4、求出协方差矩阵的特征值及对应的特征向量;
5、将特征向量按对应特征值大小从上到下按行排列成矩阵,取前 k 行组成矩阵 P;
6、
Y
=
P
X
Y=P X
Y=PX 即为降维到 k 维后的数据。
看到这里PCA就基本讲完了,那么PCA有什么问题呢?计算量太大了,协方差矩阵哎,你要是求过你就会知道。。。那么SVD就该闪亮登场了!!!
SVD(奇异值分解)
SVD的出现解决了PCA降维的最大痛点-----计算量大。看到这里,你一定知道了,那肯定是数学技巧上的革新了,没错!!!
首先看SVD的公式:
A
=
U
Σ
V
T
A=U \Sigma V^{T}
A=UΣVT其中U是一个 mxm的矩阵,Σ 是一个 mxn的矩阵,除了主对角线上的元素以外全为0,主对角线上的每个元素都称为奇异值,V是一个nxn 的矩阵。U和 V都是酉矩阵,即满足
U
T
U
=
I
,
V
T
V
=
I
U^{T} U=I, V^{T} V=I
UTU=I,VTV=I 。下图可以很形象的看出上面SVD的定义:

接下来的任务就是求出这三个矩阵!
下面就是数学的魅力了。A左乘A的转置是一个方阵,所以必可以特征分解。
(
A
T
A
)
v
i
=
λ
i
v
i
\left(A^{T} A\right) v_{i}=\lambda_{i} v_{i}
(ATA)vi=λivi
那么:
(
A
A
T
)
u
i
=
λ
i
u
i
\left(A A^{T}\right) u_{i}=\lambda_{i} u_{i}
(AAT)ui=λiui
所以这时候U跟V就求出来了(A是mxn的矩阵,那么
(
A
T
A
)
\left(A^{T} A\right)
(ATA)就是nxn的矩阵,所以
v
i
v_{i}
vi就是V矩阵,同理
u
i
u_{i}
ui就是U矩阵。)
具体证明一下:
A
=
U
Σ
V
T
⇒
A
T
=
V
Σ
U
T
⇒
A
T
A
=
V
Σ
U
T
U
Σ
V
T
=
V
Σ
2
V
T
A=U \Sigma V^{T} \Rightarrow A^{T}=V \Sigma U^{T} \Rightarrow A^{T} A=V \Sigma U^{T} U \Sigma V^{T}=V \Sigma^{2} V^{T}
A=UΣVT⇒AT=VΣUT⇒ATA=VΣUTUΣVT=VΣ2VT
那么我们只需要求出Σ矩阵就大功告成了!
其实上式已经给出Σ矩阵的解了,因为Σ矩阵出了对角线都为0,而Σ的平方是
(
A
T
A
)
\left(A^{T} A\right)
(ATA)的特征值,所以
σ
i
=
λ
i
‾
\sigma_{i}=\sqrt{\overline{\lambda_{i}}}
σi=λi.
来个具体的例子:
A
=
(
0
1
1
1
1
0
)
\mathbf{A}=\left(\begin{array}{ll}0 & 1 \\ 1 & 1 \\ 1 & 0\end{array}\right)
A=⎝⎛011110⎠⎞
那么:
A
T
A
=
(
0
1
1
1
1
0
)
(
0
1
1
1
1
0
)
=
(
2
1
1
2
)
A
A
T
=
(
0
1
1
1
1
0
)
(
0
1
1
1
1
0
)
=
(
1
1
0
1
2
1
0
1
1
)
\begin{array}{c}\mathbf{A}^{\mathbf{T}} \mathbf{A}=\left(\begin{array}{rrr}0 & 1 & 1 \\ 1 & 1 & 0\end{array}\right)\left(\begin{array}{rr}0 & 1 \\ 1 & 1 \\ 1 & 0\end{array}\right)=\left(\begin{array}{rr}2 & 1 \\ 1 & 2\end{array}\right) \\ \mathbf{A A}^{\mathbf{T}}=\left(\begin{array}{rr}0 & 1 \\ 1 & 1 \\ 1 & 0\end{array}\right)\left(\begin{array}{rrr}0 & 1 & 1 \\ 1 & 1 & 0\end{array}\right)=\left(\begin{array}{rrr}1 & 1 & 0 \\ 1 & 2 & 1 \\ 0 & 1 & 1\end{array}\right)\end{array}
ATA=(011110)⎝⎛011110⎠⎞=(2112)AAT=⎝⎛011110⎠⎞(011110)=⎝⎛110121011⎠⎞
然后求出 A T A A^{T} A ATA的特征向量:
λ 1 = 3 ; v 1 = ( 1 / 2 1 / 2 ) ; λ 2 = 1 ; v 2 = ( − 1 / 2 1 / 2 ) \lambda_{1}=3 ; v_{1}=\left(\begin{array}{c}1 / \sqrt{2} \\ 1 / \sqrt{2}\end{array}\right) ; \lambda_{2}=1 ; v_{2}=\left(\begin{array}{c}-1 / \sqrt{2} \\ 1 / \sqrt{2}\end{array}\right) λ1=3;v1=(1/21/2);λ2=1;v2=(−1/21/2)
求出 A A T AA^{T} AAT的特征向量:
λ 1 = 3 ; u 1 = ( 1 / 6 2 / 6 1 / 6 ) ; λ 2 = 1 ; u 2 = ( 1 / 2 0 − 1 / 2 ) ; λ 3 = 0 ; u 3 = ( 1 / 3 − 1 / 3 1 / 3 ) \lambda_{1}=3 ; u_{1}=\left(\begin{array}{c}1 / \sqrt{6} \\ 2 / \sqrt{6} \\ 1 / \sqrt{6}\end{array}\right) ; \lambda_{2}=1 ; u_{2}=\left(\begin{array}{c}1 / \sqrt{2} \\ 0 \\ -1 / \sqrt{2}\end{array}\right) ; \lambda_{3}=0 ; u_{3}=\left(\begin{array}{c}1 / \sqrt{3} \\ -1 / \sqrt{3} \\ 1 / \sqrt{3}\end{array}\right) λ1=3;u1=⎝⎛1/62/61/6⎠⎞;λ2=1;u2=⎝⎛1/20−1/2⎠⎞;λ3=0;u3=⎝⎛1/3−1/31/3⎠⎞
根据 σ i = λ i \sigma_{i}=\sqrt{\lambda_{i}} σi=λi求出特征值为 3 \sqrt{3} 3和1。
所以最后有:
A
=
U
Σ
V
T
=
(
1
/
6
1
/
2
1
/
3
2
/
6
0
−
1
/
3
1
/
6
−
1
/
2
1
/
3
)
(
3
0
0
1
0
0
)
(
1
/
2
1
/
2
−
1
/
2
1
/
2
)
A=U \Sigma V^{T}=\left(\begin{array}{ccc}1 / \sqrt{6} & 1 / \sqrt{2} & 1 / \sqrt{3} \\ 2 / \sqrt{6} & 0 & -1 / \sqrt{3} \\ 1 / \sqrt{6} & -1 / \sqrt{2} & 1 / \sqrt{3}\end{array}\right)\left(\begin{array}{cc}\sqrt{3} & 0 \\ 0 & 1 \\ 0 & 0\end{array}\right)\left(\begin{array}{cc}1 / \sqrt{2} & 1 / \sqrt{2} \\ -1 / \sqrt{2} & 1 / \sqrt{2}\end{array}\right)
A=UΣVT=⎝⎛1/62/61/61/20−1/21/3−1/31/3⎠⎞⎝⎛300010⎠⎞(1/2−1/21/21/2)






















 727
727











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








