模拟用户弧线滑动，算法python实现

前言

用自动化软件执行脚本时，其中拖拽、滑动等这些操作往往是直线，而实际用户滑动时一般都不是直线，可能是一段弧线或者更复杂的线。

下面就介绍一种计算两个点直线弧线路径的方法，并通过 python 和 sikuli 实现弧线滑动

弧线坐标计算

已知 A、B两点坐标分别为(x1,y1)、（x2,y2），求经过A、B两点的弧线，显然这样的弧线有无数条，需要再加上限定条件，弧线的弧度φ，也就是A、B两点和圆心连线的夹角，范围是(0, π)，限定弧度后，这样的弧线就只剩两条了。

1. 求出圆心坐标

如图，先考虑B在A右上方，弧线位于AB下方的情况：

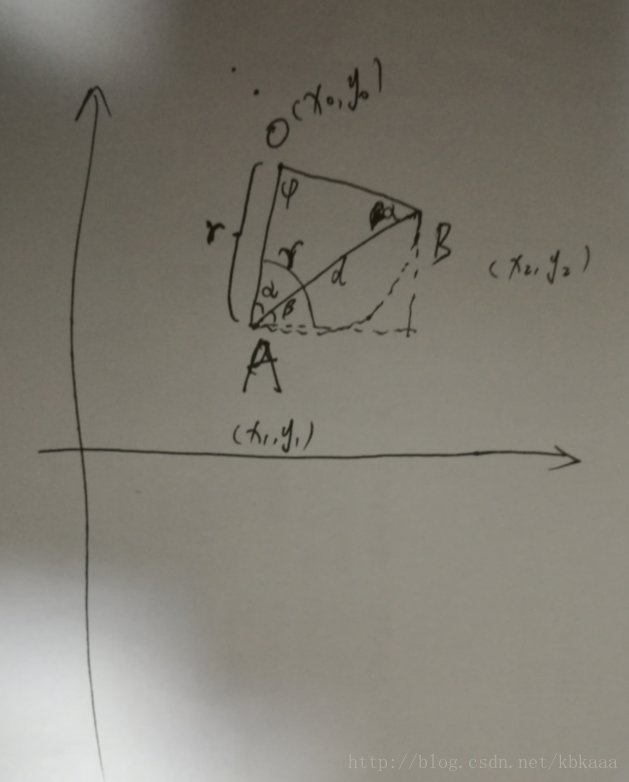
一开始想用圆心坐标列二元二次方程组，比较麻烦，就改用三角函数来运算，效果很好。主要思路就是求出其中一条半径 OA的长度和斜率，再通过 A 点坐标增量的方式求出圆心 O 的坐标

AB的长度 d = ((x2-x1)^2 + (y2-y1)^2) ^(1/2)
OA与AB的夹角 α= (π - φ)/2
根据正弦定理求半径 r = d/sinα* sinφ
AB与x轴的夹角 β= arctan((y2-y1)/(x2-x1))
OA与x轴的夹角 γ=α+β
最后O点坐标为 (x0, y0) = (x1+r*cosinγ, y1+r*sinγ)

其他情况处理：
图中各条线的相对位置只是一种情况，其他情况计算公式可能稍有不同，某些地