激活函数是用来加入非线性因素的,解决线性模型所不能解决的问题
激活函数通常有以下性质
– 非线性
– 可微性
– 单调性
– 𝑓 𝑥 ≈ 𝑥
– 输出值范围
– 计算简单
– 归一化
1.Sigmoid 函数
Sigmoid函数由下列公式定义
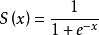
Sigmoid函数的图形如S曲线

其对x的导数可以用自身表示:
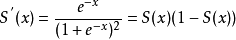
Sigmoid导数的图形如下
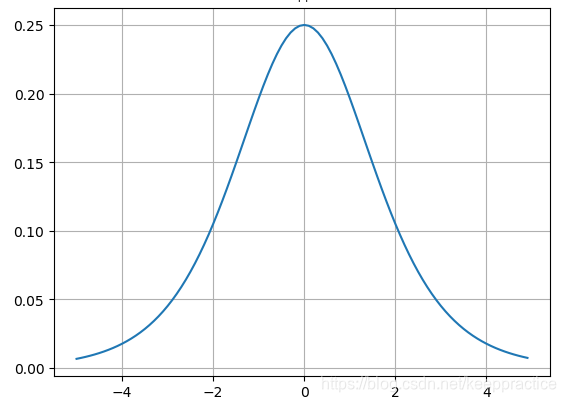
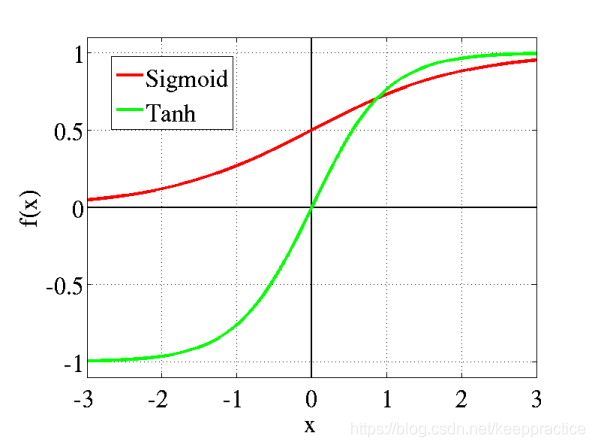
优点:平滑、易于求导。值域在0和1之间, 函数具有非常好的对称性
缺点:
1)激活函数计算量大,反向传播求误差梯度时,求导涉及除法;
2)反向传播时,很容易就会出现梯度消失的情况,从而无法完成深层网络的训练。
(由于反向传播过程中需要计算偏导数,通过求导可以得到sigmoid函数导数的最大值为0.25,如果使用sigmoid函数的话,每一层的反向传播都会使梯度最少变为原来的四分之一,当层数比较多的时候可能会造成梯度消失,从而模型无法收敛。)
代码实现
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1/(1+np.exp(-x))
def derivation_sigmoid(x):
return sigmoid(x)*(1-sigmoid(x))
def show_sigmoid_line():
x = np.arange(-10., 10., 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.grid(True)
plt.show()
def show_derivative_sigmoid():
x = np.arange(-5., 5., 0.1)
y = derivation_sigmoid(x)
plt.plot(x, y)
plt.grid(True)
plt.show()
def show_derivative_sigmoid_and_sigmoid():
x = np.arange(-5., 5., 0.1)
y = derivation_sigmoid(x)
y1 = sigmoid(x)
plt.plot(x, y)
plt.plot(x, y1)
plt.grid(True)
plt.show()
if __name__ == '__main__':
show_sigmoid_line()
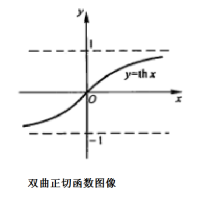
2. 双曲正切函数(tanh)
tanh函数由下列公式定义
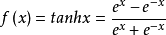
tanh函数的图形
tanh函数导数
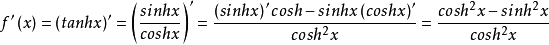
f
1
(
x
)
=
1
cosh
2
x
=
1
−
tanh
2
x
f ^1(x) = \frac{1}{\cosh^2x} = 1-\tanh^2x
f1(x)=cosh2x1=1−tanh2x
Tanh函数导数的图形
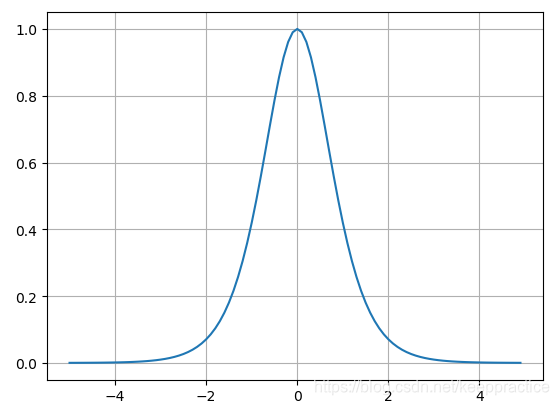
tanh也是一种非常常见的激活函数。与sigmoid相比,它的输出均值是0,使得其收敛速度要比sigmoid快,减少迭代次数。然而,从途中可以看出,tanh一样具有软饱和性,从而造成梯度消失
import numpy as np
import matplotlib.pyplot as plt
def tanh(x):
return (np.exp(x)-np.exp(-x))/(np.exp(x)+np.exp(-x))
def derivation_tanh(x):
return (1-tanh(x)*tanh(x))
#return (1 - np.square(tanh(x)))
def show_tanh_line():
x = np.arange(-10., 10., 0.1)
y = tanh(x)
plt.plot(x, y)
plt.grid(True)
plt.show()
def show_derivative_tanh():
x = np.arange(-5., 5., 0.1)
y = derivation_tanh(x)
plt.plot(x, y)
plt.grid(True)
plt.show()
if __name__ == '__main__':
show_derivative_tanh()
3. Relu 函数
relu 函数由下列公式定义
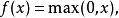
图形
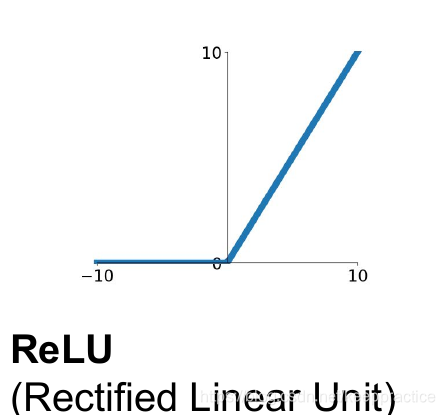
在神经网络中,线性整流作为神经元的激活函数,定义了该神经元在线性变换
w
T
x
+
b
w^Tx+b
wTx+b之后的非线性输出结果。换言之,对于进入神经元的来自上一层神经网络的输入向量,使用线性整流激活函数的神经元会输出
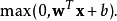
CNN中常用。对正数原样输出,负数直接置零。在正数不饱和,在负数硬饱和。relu计算上比sigmoid或者tanh更省计算量,因为不用exp,因而收敛较快。但是还是非zero-centered。
relu在负数区域被kill的现象叫做dead relu,这样的情况下,有人通过初始化的时候用一个稍微大于零的数比如0.01来初始化神经元,从而使得relu更偏向于激活而不是死掉,但是这个方法是否有效有争议
优点:
- 更加有效率的梯度下降以及反向传播:避免了梯度爆炸和梯度消失问题
- 简化计算过程:没有了其他复杂激活函数中诸如指数函数的影响;同时活跃度的分散性使得神经网络整体计算成本下降
4. Leaky ReLU函数
在输入值为负的时候,带泄露线性整流函数(Leaky ReLU)的梯度为一个常数,而不是0。在输入值为正的时候,带泄露线性整流函数和普通斜坡函数保持一致。换言之,
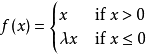
图形
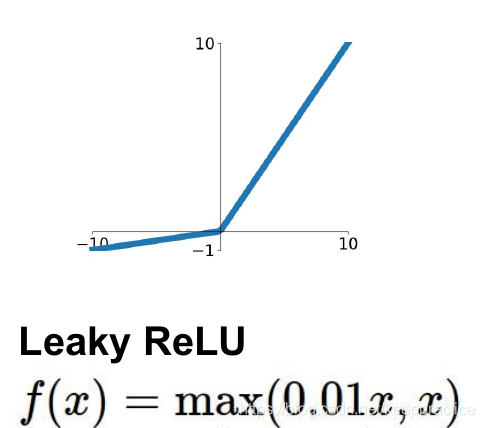
为了解决上述的dead ReLU现象。这里选择一个数,让负数区域不在饱和死掉。这里的斜率都是确定的。
5. PReLU
parametric rectifier:
f(x) = max(ax,x)
但是这里的a不是固定下来的,而是可学习的。
6. ELU
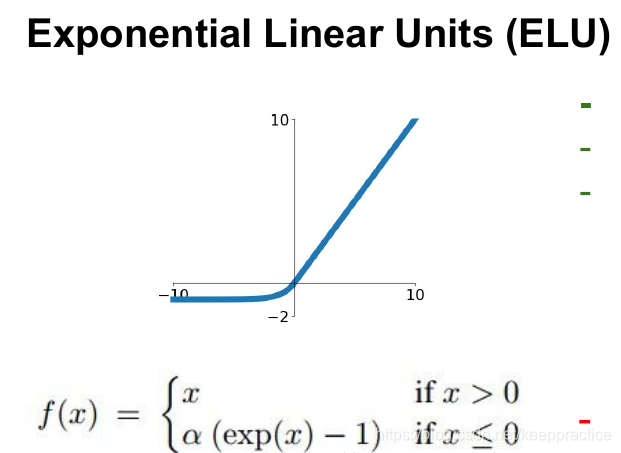
具有relu的优势,且输出均值接近零,实际上prelu和LeakyReLU都有这一优点。有负数饱和区域,从而对噪声有一些鲁棒性。可以看做是介于relu和LeakyReLU之间的一个东西。当然,这个函数也需要计算exp,从而计算量上更大一些。
7. 大一统:Maxout
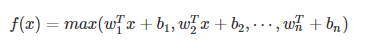
Maxout模型实际上也是一种新型的激活函数,在前馈式神经网络中,Maxout的输出即取该层的最大值,在卷积神经网络中,一个Maxout feature map可以是由多个feature map取最值得到。
maxout的拟合能力是非常强的,它可以拟合任意的的凸函数。但是它同dropout一样需要人为设定一个k值。
为了便于理解,假设有一个在第i层有2个节点第(i+1)层有1个节点构成的神经网络。
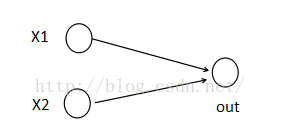
激活值 out = f(W.X+b); f是激活函数。’.’在这里代表內积
X
=
(
x
1
,
x
2
)
T
,
W
=
(
w
1
,
w
2
)
T
X=(x1,x2)^T, W=(w1,w2)^T
X=(x1,x2)T,W=(w1,w2)T
那么当我们对(i+1)层使用maxout(设定k=5)然后再输出的时候,情况就发生了改变。
缺点在于增加了参数量。
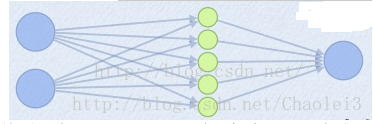
此时网络形式上就变成上面的样子,用公式表现出来就是:
z1 = W1.X+b1;
z2 = W2.X+b2;
z3 = W3.X+b3;
z4 = W4.X+b4;
z5 = W5.X+b5;
out = max(z1,z2,z3,z4,z5);
也就是说第(i+1)层的激活值计算了5次,可我们明明只需要1个激活值,那么我们该怎么办?其实上面的叙述中已经给出了答案,取这5者的最大值来作为最终的结果。
总结一下,maxout明显增加了网络的计算量,使得应用maxout的层的参数个数成k倍增加,原本只需要1组就可以,采用maxout之后就需要k倍了。
再叙述一个稍微复杂点的应用maxout的网络,网络图如下:
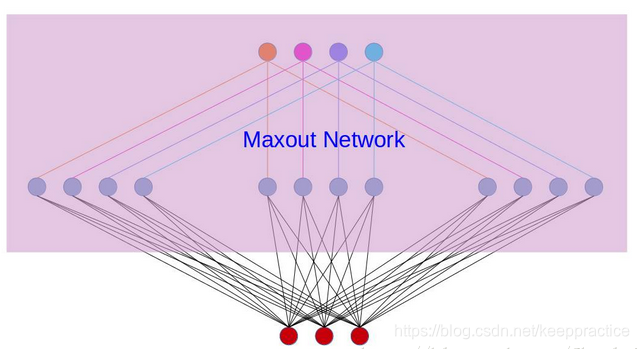
对上图做个说明,第i层有3个节点,红点表示,而第(i+1)层有4个结点,用彩色点表示,此时在第(i+1)层采用maxout(k=3)。我们看到第(i+1)层的每个节点的激活值都有3个值,3次计算的最大值才是对应点的最终激活值。我举这个例子主要是为了说明,决定结点的激活值的时候并不是以层为单位,仍然以节点为单位。
8. Softmax 函数
S i = e z i ∑ k e z k S_i = \frac{e^{z_i}}{ \sum_{k}e^{z_k}} Si=∑kezkezi
Softmax函数求导
∂
s
j
∂
z
i
=
{
s
i
(
1
−
s
i
)
,
当 i = j 时
−
s
i
s
j
,
当 i != j 时
\frac{\partial s_j}{\partial z_i}= \begin{cases} s_i(1-s_i), & \text {当 i = j 时} \\ -s_is_j, & \text{当 i != j 时} \end{cases}
∂zi∂sj={si(1−si),−sisj,当 i = j 时当 i != j 时
其中:
s
i
s_i
si 指Softmax求的值
z
i
z_i
zi 指隐层输出值
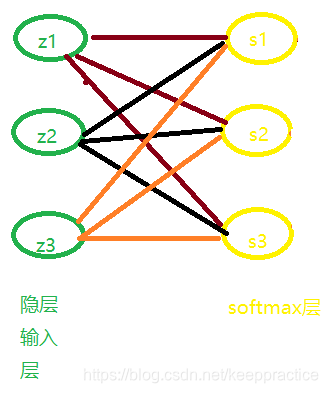
推导过程
当 i = j 时
∂
s
j
∂
z
i
=
∂
(
e
i
z
∑
k
e
z
k
)
∂
z
i
=
∑
k
e
z
k
e
z
i
−
(
e
z
i
)
2
(
∑
k
e
z
k
)
2
=
(
e
z
i
∑
k
e
z
k
)
(
1
−
e
z
i
∑
k
e
z
k
)
=
s
i
(
1
−
s
i
)
\frac{\partial s_j}{\partial z_i}=\frac{\partial ({\frac{e^z_i}{\sum_k e^{z_k}})}}{\partial z_i}= \frac{\sum_ke^{z_k}e^{z_i}-(e^{z_i})^2}{(\sum_ke^{z_k})^2}=(\frac{e^{z_i}}{\sum_ke^{z_k}})(1-\frac{e^{z_i}}{\sum_ke^{z_k}}) = s_i(1-s_i)
∂zi∂sj=∂zi∂(∑kezkeiz)=(∑kezk)2∑kezkezi−(ezi)2=(∑kezkezi)(1−∑kezkezi)=si(1−si)
当 i != j 时
∂
s
j
∂
z
i
=
∂
(
e
j
z
∑
k
e
z
k
)
∂
z
i
=
(
−
e
z
j
e
z
i
)
(
∑
k
e
z
k
)
2
=
(
−
e
z
i
∑
k
e
z
k
)
(
e
z
i
∑
k
e
z
k
)
=
−
s
i
s
j
\frac{\partial s_j}{\partial z_i}=\frac{\partial ({\frac{e^z_j}{\sum_k e^{z_k}})}}{\partial z_i}=\frac{(-e^{z_j}e^{z_i})}{(\sum_ke^{z_k})^2}=(-\frac{e^{z_i}}{\sum_ke^{z_k}})(\frac{e^{z_i}}{\sum_ke^{z_k}}) =- s_is_j
∂zi∂sj=∂zi∂(∑kezkejz)=(∑kezk)2(−ezjezi)=(−∑kezkezi)(∑kezkezi)=−sisj
9. 隐层经过Softmax与交叉熵函数 的导数是
∂
L
∂
z
i
=
s
i
−
y
i
\frac{\partial L}{\partial z_i} =s_i-y_i
∂zi∂L=si−yi
其中
y
i
y_i
yi 指期望值(真实值)
s
i
s_i
si 指Softmax求的值
z
i
z_i
zi 指隐层输出值
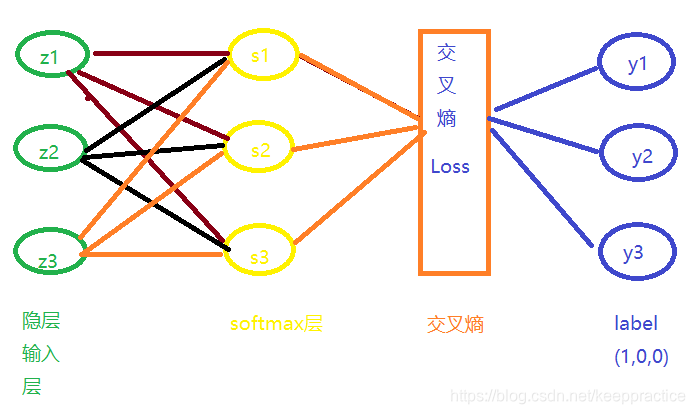
隐层经过Softmax与交叉熵函数 求导的推到过程
推导之前要了解的知识
y
i
y_i
yi 指期望值(真实值)
s
i
s_i
si 指Softmax求的值
z
i
z_i
zi 指隐层输出值
Loss 对神经元输出
z
i
z_i
zi的梯度记为
∂
L
∂
Z
i
\frac{\partial L}{\partial Z_i}
∂Zi∂L
Softmax 函数
S
i
=
e
z
i
∑
k
e
z
k
S_i = \frac{e^{z_i}}{\sum_ke^{z_k}}
Si=∑kezkezi
交叉熵损失函数
L
o
s
s
=
−
∑
i
y
i
l
n
s
i
Loss=−\sum_i y_i lns_i
Loss=−i∑yilnsi
开始推导
∂
L
i
∂
x
i
=
−
y
i
S
i
\frac{\partial L_i}{\partial x_i} = \frac{-y_i}{Si}
∂xi∂Li=Si−yi
记为 (1) 式
根据复合函数求导法则:
∂
L
∂
z
i
=
∑
j
(
∂
L
j
∂
s
j
∗
∂
s
j
∂
z
i
)
\frac{\partial L}{\partial z_i} = \sum_j(\frac{\partial L_j}{\partial s_j}*\frac{\partial s_j}{\partial z_i} )
∂zi∂L=j∑(∂sj∂Lj∗∂zi∂sj)
其中
L
i
=
−
y
i
ln
s
i
L_i=-y_i\ln{s_i}
Li=−yilnsi
由于
当 i = j 时
∂
s
j
∂
z
i
=
∂
(
e
i
z
∑
k
e
z
k
)
∂
z
i
=
∑
k
e
z
k
e
z
i
−
(
e
z
i
)
2
(
∑
k
e
z
k
)
2
=
(
e
z
i
∑
k
e
z
k
)
(
1
−
e
z
i
∑
k
e
z
k
)
=
s
i
(
1
−
s
i
)
\frac{\partial s_j}{\partial z_i}=\frac{\partial ({\frac{e^z_i}{\sum_k e^{z_k}})}}{\partial z_i}= \frac{\sum_ke^{z_k}e^{z_i}-(e^{z_i})^2}{(\sum_ke^{z_k})^2}=(\frac{e^{z_i}}{\sum_ke^{z_k}})(1-\frac{e^{z_i}}{\sum_ke^{z_k}}) = s_i(1-s_i)
∂zi∂sj=∂zi∂(∑kezkeiz)=(∑kezk)2∑kezkezi−(ezi)2=(∑kezkezi)(1−∑kezkezi)=si(1−si)
记为 (2) 式
当 i != j 时
∂
s
j
∂
z
i
=
∂
(
e
j
z
∑
k
e
z
k
)
∂
z
i
=
(
−
e
z
j
e
z
i
)
(
∑
k
e
z
k
)
2
=
(
−
e
z
i
∑
k
e
z
k
)
(
e
z
i
∑
k
e
z
k
)
=
−
s
i
s
j
\frac{\partial s_j}{\partial z_i}=\frac{\partial ({\frac{e^z_j}{\sum_k e^{z_k}})}}{\partial z_i}=\frac{(-e^{z_j}e^{z_i})}{(\sum_ke^{z_k})^2}=(-\frac{e^{z_i}}{\sum_ke^{z_k}})(\frac{e^{z_i}}{\sum_ke^{z_k}}) =- s_is_j
∂zi∂sj=∂zi∂(∑kezkejz)=(∑kezk)2(−ezjezi)=(−∑kezkezi)(∑kezkezi)=−sisj
记为 (3) 式
故:
∂
L
∂
z
i
=
∑
j
(
∂
L
j
∂
s
j
∂
s
j
∂
z
i
)
=
∑
j
!
=
i
(
∂
L
j
∂
s
j
∂
s
j
∂
z
i
)
+
∑
j
=
i
(
∂
L
j
∂
s
i
∂
s
i
∂
z
i
)
\frac{\partial L}{\partial z_i} = \sum_j(\frac{\partial L_j}{\partial s_j}\frac{\partial s_j}{\partial z_i} )=\sum_{j!=i} (\frac{\partial L_j}{\partial s_j} \frac{\partial s_j}{\partial z_i}) + \sum_{j=i}(\frac{\partial L_j}{\partial s_i}\frac{\partial s_i}{\partial z_i})
∂zi∂L=j∑(∂sj∂Lj∂zi∂sj)=j!=i∑(∂sj∂Lj∂zi∂sj)+j=i∑(∂si∂Lj∂zi∂si)
代入(1)(2)(3)得
=
∑
j
!
=
i
(
−
y
j
s
j
)
(
−
s
i
s
j
)
+
s
i
(
1
−
s
i
)
=
∑
j
!
=
i
(
y
j
)
(
−
s
i
)
+
s
i
(
1
−
s
i
)
=
s
i
∑
j
y
j
−
y
i
= \sum_{j!=i}(-\frac{y_j}{s_j})(-s_is_j) +s_i(1-s_i) = \sum_{j!=i}(y_j)(-s_i)+s_i(1-s_i) = s_i\sum_jy_j-y_i
=j!=i∑(−sjyj)(−sisj)+si(1−si)=j!=i∑(yj)(−si)+si(1−si)=sij∑yj−yi
由于
y
i
y_i
yi 最终只有一个类别是1,其它类型都是0。因此对于分类问题这个梯度就等于
∂
L
∂
z
i
=
s
i
−
y
i
\frac{\partial L}{\partial z_i} =s_i-y_i
∂zi∂L=si−yi
参考
https://blog.csdn.net/edogawachia/article/details/80043673
https://www.cnblogs.com/missidiot/p/9378079.html
https://blog.csdn.net/u013230189/article/details/82799469
https://m.sohu.com/a/209844518_609569/?pvid=000115_3w_a






















 7417
7417











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










