八皇后问题是一个经典的问题,其核心是:在n*n的棋盘上,有n个皇后,这些皇后必须位于不同行不同列上,并且不能处于同一对角线上,否则会因相互攻击而死亡。那么如何安排皇后们的位置呢?
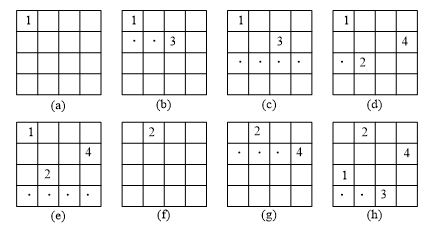
我们可以利用回溯法,先确定第一个皇后的位置,之后进入下一行,确定第二个皇后的位置,再之后进入下一行,如果发现找不到一个位置安排新皇后,则回退到上一行,将上一行的皇后向后移动一列,再考虑下一行的皇后,如此循环,直到安排好所有的皇后为止。附上一张图片以便于理解。
具体实现的代码及所遇到的问题及解决如下:
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
typedef int status;
/*打印答案*/
status printsolution(int *x,int n){
int i=1,j=1;
for(i=1;i<=n;i++){
for(j=1;j<=n;j++){
/*如果该列可以放皇后,打印“Q”*/
if(j==x[i])
printf("Q");
else
printf("*");//不能则打印星号
}
printf("\n");
}
printf("\n");
}
status isplace(int *x,int k){
int i=1;//从第一行开始考察
/*考察前k-1行*/
for(i=1;i<=k-1;i++){
/*这是皇后相互攻击的条件*/
if((x[i]==x[k])||(fabs(x[i]-x[k])==fabs(i-k)))
return FALSE;
}
return OK;
}
status nqueen(int *x,int n){
int k=1;
x[k]=0;//先让x[k]=0,进入循环后加1
while(k>0){//全部行列判断完后,k=0
x[k]++;
while(x[k]<=n&&!isplace(x,k))//寻找可以放的列
x[k]++;
if(x[k]<=n){//如果找到
if(k==n)//k==n说明是完整解
printsolution(x,n);
else{//k<n是不完整解
k++;//移动到下一行继续判断
x[k]=0;//移动到下一行之后要注意将x[k]置为0,以便从第一行开始判断
}
}
else//x[k]如果大于n,则不必考虑此行,k--回溯到上一行
k--;
}
}
int main(void){
int * x;
int num=0;
x=(int *)malloc(sizeof(int)*(num+1));//这里用动态数组存储可以放置皇后的列
printf("请输入皇后数目");
scanf("%d",&num);
nqueen(x,num);
}2016/4/15更新:
今天复习了八皇后问题,在此过程中发现了不少之前忽视的问题,下面加以总结以便回顾反思。
问题主要出现在status nqueen()函数中
status nqueen(int *x,int n){
int i=1;
x[i]=0;
while(i>0){
x[i]++;
while(x[i]<=n&&!isplace(x,i))
x[i]++;
if(x[i]<=n){//此处进行判断的条件是x[i]<=n,因为前一步在寻找能够放皇后的列
if(i==n)//这一步的判断条件为i==n,因为x[i]==n不能说明找到了完整解,这两处很容易出错,今后应谨慎对待
printsolution(x,n);
else{
i++;
x[i]=0;//这一步在移动到下一行时一定要让列置为0
}
}
else
i--;
}
}
























 3961
3961

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








