三种静态查找的思路及具体实现

一.查找及其相关概念

查找,就是根据给定的某个值，在查找表中确定一个关键字等于数据值的数据元素的过程

查找表按操作方式可分为两种:
静态查找表:只做查找操作的查找表
动态查找表:在查找过程中插入新的数据元素或删除原有的数据元素

二.静态查找的三种具体方式

1.顺序查找算法

顺序查找，也称线性查找，是从第一个元素开始，将后面的每个元素与给定元素进行比对，若相同，则返回该元素;若没有与之相同的元素，返回空

#include<stdio.h>
#include<stdlib.h>
#include<time.h> 
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define MAXSIZE 100 
typedef int Status;
typedef int ElemType;

/*线性查找*/ 
Status SeqSearch(ElemType *a,int num,ElemType key){
    int i=0;
    for(i;i<num;i++){
        if(a[i]==key)
           return i+1;
    }
    return ERROR;
}

int main(void){
    ElemType arr[11]={0,1,16,24,35,47,59,62,73,88,99};
    srand(time(0));
    int i=rand()%11;
    printf("查找值为%d的元素，位序为%d\n",arr[i],SeqSearch(arr,11,arr[i]));
}

代码很简单，调用rand函数是用来随机生成数组索引的

线性查找是最简单的查找方式，但一般来说越简单的东西时间效率往往不会太高，例如简单的冒泡排序。那么我们如何对这个算法进行优化呢？我们注意到在代码中每次for循环中都会进行i是否越界的比较，那么我们可以这样修改

/*优化后的线性查找*/
Status SeqSearch2(ElemType *a,int num,ElemType key){
    int i=num-1;/*从最后一位开始查找*/
    a[0]=key;/*设置a[0]为关键字位，也称为“哨兵”*/
    while(a[i]!=key){
        i--;
    }
    return i;/*这个算法相当于浪费a[0]位，所以查到的位序比第一种算法少1*/
}
int main(void){
    ElemType arr[11]={0,1,16,24,35,47,59,62,73,88,99};
    srand(time(0));
    int j=rand()%11+1;
    int Status=SeqSearch2(arr,11,arr[j]);
    if(Status)
       printf("查找值为%d的元素，位序为%d\n",arr[j],Status);
    else
       printf("查找失败\n");
}

这种方法通过在尽头设置哨兵，免去了每次都要判断是否越界的过程，在数据量较大时，这个算法与前一种算法的差异将非常大
顺序查找最后的情况是第一次查找就找到，时间复杂度为O(1),最差为O(n),平均来说，时间复杂度为O(n)

2.二分查找

二分查找要求查找表中的数据的关键码必须有序(通常要按从小到大排列)，必须使用线性结构存储;具体思路是，将关键值与中间元素作比较，若大于中间元素，则在右半区中继续查找；若小于中间元素，则在左半区继续查找，直到找到或失败为止

Status BinarySearch(ElemType *a,int num,ElemType key){
    int low=0,high=num-1,mid=0;
    while(low<=high){
        mid=(low+high)/2;/*折半*/
        if(key<a[mid])/*在左半区*/ 
          high=mid-1;
        else if(key>a[mid])
          low=mid+1;
        else
          return mid+1;
    }
    return ERROR;
}
int main(void){
    ElemType arr[11]={0,1,16,24,35,47,59,62,73,88,99};
    srand(time(0));
    int i=rand()%11;
    int j=rand()%11+1;Status= BinarySearch(arr,11,arr[j]);
    if(Status)
        printf("二分查找值为%d的元素，位序为%d\n",arr[j],Status);
    else
        printf("查找失败\n");
}

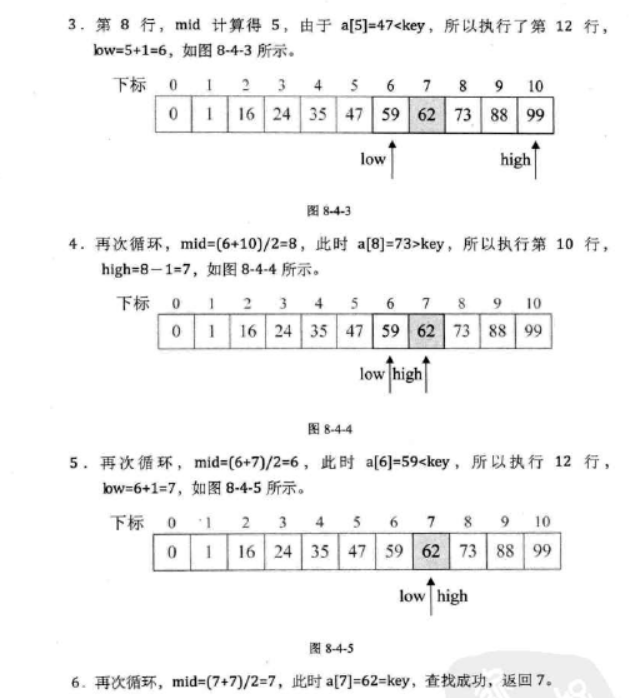
上图清晰地分析了整个算法的执行过程，图片来自《大话数据结构》

3.插值查找

想象这样一个，我们要在英文词典中查询apple这个单词，我们很自然的会从前几页开始翻，而查zoo这个单词时，我们会从后几页开始翻。但如果使用二分查找算法呢？只会机械地从中间开始翻，然后逐步缩小范围，如果要查询第一个数据或最后一个数据这种极端情况，二分查找就显得不再合适了。
鉴于此种情况，伟大的数学家们开始思考如何改进这个算法，之后，发现了这样的情况:

如果将mid=(low+high)/2稍作变换，就可以得到mid=low+(high-low)/2
换句话说，二分查找中的mid等于 最低下表low加上high和low差值的一半，数学家们从这个”1/2”入手，做出了如下的改进:

mid=low+ (high-low)*(key-a[low])/(a[high]-a[low])

单纯从时间复杂度上看，它和二分查找相同,均为对数级算法，但是对于表长大且关键词分布均匀的情况，它的平均性能优于二分查找，但遇到一些极端数据的情况，插值查找也不一定是好的选择。

/*插值查找算法*/
Status Interpolation(ElemType *a,int num,ElemType key){
    int low=1,high=num-1,mid=0;
    while(low<=high){
        mid=low+ (high-low)*(key-a[low])/(a[high]-a[low]); /* 插值 */
        if(key<a[mid])/*在左半区*/ 
          high=mid-1;
        else if(key>a[mid])
          low=mid+1;
        else
          return mid+1;
    }
    return ERROR;
}
int main(void){
    ElemType arr[11]={0,1,16,24,35,47,59,62,73,88,99};
    srand(time(0));
    int i=rand()%11;
    int j=rand()%11+1;  
        Status=Interpolation(arr,11,arr[j]);
    if(Status)
        printf("插值查找值为%d的元素，位序为%d\n",arr[j],Status);
    else
        printf("查找失败\n");
}

4.Fabbonaci查找

1.查找思想::

假设查找表中的某个数据比某个Fabbonaci数小1，用low，high，mid分别表示查找表下界，上界和分割位置，当:

key<a[mid]时，调整到左半区
key>a[mid]时，调整到左半区
key==a[mid]时，返回mid，查找成功

代码如下:

Status FabbonaciSearch(ElemType *a,int num,ElemType key){
    int high=num,low=1,mid=0,k=0,i=0;
    while(num>Fab[k]-1)//第一步先计算num在Fabbonaci数列中的位置 
       k++;
    for(i=num;i<Fab[k];i++)/*将数组a中未初始化的数据补全*/
       a[i]=a[num];
    while(low<=high){
        mid=low+Fab[k-1]-1;
        /*调整到右半区时,k减小2*/
        if(key>a[mid]){
            low=mid+1;
            k=k-2;
        }
        /*调整到左半区时，k的值减小1*/
        else if(key<a[mid]){
            high=mid-1;
            k=k-1;
        }
        /*如果k==mid，说明查找成功*/
        else{
            if(mid<=num)
               return mid;
            else
               return num;/*若mid>num,说明是补全的数据，返回n*/
        }
    }
    return 0;
}
int main(void){
    ElemType arr[11]={0,1,16,24,35,47,59,62,73,88,99};
    for(int i=0;i<20;i++){
        Fab[i]=Fabbonaci(i);
    } 
    srand(time(0));
    int i=rand()%11;
    int j=rand()%11+1;  
        Status=FabbonaciSearch(arr,10,arr[j]);
    if(Status)  
        printf("Fabbnaci查找值为%d的元素，位序为%d\n",arr[j],Status);
    else
        printf("查找失败\n");

}

这两张图片清晰地显示了算法运行的过程

注意到在确定num在Fabbonaci数列中的位置的循环之后，有一个补全数据的循环，这个循环的作用在于，当key值为99时，第一步的mid=8，a[8]小于99，需要调整到右半区，则low=mid+1,即low=9，所以mid的新值为9+Fab[4]-1=11。但a[11]并没有初始化，其内部是一个随机值，这个时候用key与a[11]作比较就会产生不可预知的后果，所以我们要加上一个补全数据的循环，这是这个算法中一个令人难以理解的部分，需要在纸上一步步演绎才能理解其内部的巧妙

Fabbonaci查找的时间复杂度为O(logn)，看似与二分，插值查找相同，但由于Fabbonaci中的mid值只需要进行简单的加减运算，当数据量巨大的时候，这个差异就会被成倍放大,三种查找各有优劣，使用前应加以考虑